LA LEZIONE
La conduzione e la resistenza termica
Se si prende in considerazione un appartamento riscaldato dai radiatori in inverno, per
intervalli di tempo non troppo lunghi la temperatura dell’aria all’interno di una stanza e
quella dell’aria esterna possono essere considerate costanti. In altre parole la
differenza di temperatura DT=Ti-Te non è funzione del tempo. Il calore Q che fluisce
attraverso le pareti dall’interno verso l’esterno è compensato dall’energia radiante dei
termosifoni dell’impianto termico. Il processo è stazionario. La parete o l’infisso
confinante con l’esterno ha le due facce piane di area S a diversa temperatura e ciò
causa nell’intervallo di tempo Dt, un flusso di calore Q/ Dt proporzionale al salto termico
DT. La presenza del vetro rispetto alla parete provoca un aumento del flusso a causa
dell’incremento delle proprietà conduttrici, tanto più grande quanto è sottile lo spessore
l del materiale.
L’insieme di queste condizioni è riassunto nell’espressione:
lS DT/l = Q/Dt
con lsimbolo del coefficiente di conducibilità (o conduttività) termica del materiale,
misurato in W/m K.1
Paragonando la conduzione termica alla conduzione elettrica, il flusso di calore diviene
il flusso di cariche (l’intensità della corrente elettrica); la causa del flusso termico è il
salto termico, mentre nel caso elettrico è la differenza di potenziale DV. Le leggi di
Ohm:
DV = R I
R = r l/S
con r resistività elettrica, sono completamente equivalenti alla precedente espressione
termica e quindi viene spontaneo, assumendo la resistività come il reciproco della
conduttività, associare al concetto di resistenza termica RT il rapporto: l/(l S).
Il paragone può essere spinto oltre considerando una parete a più strati come una
somma di resistenze termiche. In analogia ai resistori in serie elettrici, la resistenza
termica complessiva RT è uguale alla somma delle singole resistenze termiche
RT1+RT2+RT3 dei diversi materiali omogenei aventi ciascuno il suo spessore caratteristico
e la sua conducibilità (e uguale area), con una dimostrazione del tutto analoga al caso
elettrico legata alla stazionarietà del flusso.
Tuttavia si preferisce nella maggioranza delle trattazioni tecniche, per eliminare il
problema della trasmissione di calore attraverso il bordo della superficie piana,
assumere un’area sufficientemente estesa (al limite una parete piana di estensione
infinita) così la resistenza termica di ogni singolo componente omogeneo di spessore l e
conducibilità l viene definita secondo l’espressione:RT = l/l .La resistenza termica non
contiene così il termine dovuto all’area e ha l’unità di misura
K m2 / W.
1
L’unità di misura della conduttività watt/(metro kelvin) è espressa seguendo il Sistema Internazionale. Va
notato che nell’espressione del calore compare la variazione di temperatura. Poiché a una differenza di
temperatura di 10 K corrisponde una variazione di 10 °C, è possibile sostituire i kelvin con i gradi Celsius.
Il coefficiente di conducibilità di un materiale dipende dalla sua struttura molecolare e
macromolecolare. In genere i materiali molto densi hanno un’elevata conducibilità,
mentre i materiali fibrosi o con celle di piccolissime dimensioni sono degli ottimi isolanti
termici. Un esempio limite è costituito dagli aerogel la cui struttura è rappresentata
nella figura che segue, un insieme di microsfere di diametro prossimo a pochi
milionesimi di metro.
Questi materiali hanno la più bassa conduttività e si presentano macroscopicamente
come una sorta di fumo solido (gli inglesi li chiamano frozen smoke – fumo ghiacciato).
Nella terza figura sono mostrate le eccezionali proprietà isolanti di un aerogel di silice
che protegge un fiore dal calore di una fiamma.
Nell’edilizia moderna un sistema di riduzione dei consumi energetici si ottiene
attraverso la sostituzione degli infissi tradizionali con altri aventi doppi vetri separati da
un’intercapedine riempita di gas, e il rifacimento delle facciate con un sistema di
coibentazione a cappotto con materiale isolante. Nella foto che segue è rappresentata
una delle fasi di isolamento termico di un edificio con la posa in opera di un pannello
isolante dello spessore di alcuni centimetri.
La convezione e l’irraggiamento
Le analogie tra caso elettrico e termico non possono essere spinte oltre la conduzione.
Anche avendo approssimato il fenomeno al caso stazionario unidirezionale bisogna
subito correggere e complicare il modello della trasmissione del calore considerando i
fenomeni convettivi e di irraggiamento. Il trasporto di materia dei fluidi è un potente
acceleratore del flusso di calore.2
2
A esempio nella muratura con intercapedine d’aria o nei doppi vetri delle finestre, l’eventuale circolazione
dei gas aumenta notevolmente la dispersione di calore.
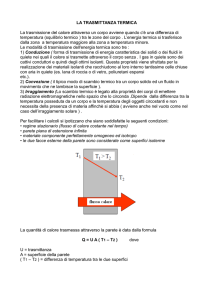
Prendiamo in esame la totalità dei fenomeni termici. Nel caso stazionario la
temperatura, in prossimità e all’interno di una parete, segue il grafico riportato in
figura.
Agli andamenti lineari all’interno del materiale (dovuti
alle variazioni di resistenza termica degli strati di materiale omogeneo) corrisponde
anche una variazione relativa a un piccolo straterello d’aria in prossimità della
superficie piana, sia all’interno della stanza che all’esterno. Queste ulteriori resistenze
non dipendono dallo spessore (strato d’aria in cui vi è la differenza T i-T1, oppure la
differenza T4-Te) e possono essere descritte dal reciproco di un coefficiente di scambio
termico a3 che tenga conto sia dei fenomeni convettivi che da quelli di irraggiamento. Il
coefficiente in questione è chiamato adduzione o coefficiente di scambio termico
liminare, per indicare lo strato superficiale più a stretto contatto con la parete. Il
coefficiente di adduzione interno ai è diverso da quello esterno ae. In città i valori
riportati nelle tabelle per una parete verticale sono ai=9 W/m2K, ae=23 W/m2K.
Consideriamo la situazione con una parete omogenea. L’ipotesi è che sulla parete
interna la temperatura T1 sia diversa da quella dell’aria nella stanza Ti, così come sulla
parete esterna la temperatura T2 sia diversa da Te.
Allora per un flusso stazionario si può scrivere:
Q/Dt=ai(Ti-T1)S per la prima variazione di temperatura,
Q/Dt=l(T1-T2)S/l per la conduzione all’interno del materiale,
Q/Dt=ae(T2-Te)S per lo scambio termico liminare esterno.
Isolando le variazioni di temperatura:
3
Il simbolo alternativo adottato da molti autori è la lettera h.
Ti-T1=Q/S Dt ai
T1-T2= Q l/S Dt l
T2-Te=Q/S Dt ae .
Infine eguagliando le somme delle variazioni delle temperature alle somme dei termini
contenenti il calore si ha:
Ti-Te= ai-1+l l-1 ae-1) Q /(S Dt) che può essere scritta, ritornando al flusso di calore:
Q/ Dt=(Ti-Te)Sai-1+ l l-1 ae-1)-1.
La grandezza K = ai-1+ l l-1 ae-1)-1 è chiamata trasmittanza termica4, mentre il suo
reciproco è la resistenza termica RT = ai-1+ l l-1 ae-1). Il flusso di calore complessivo è
direttamente proporzionale alla differenza di temperatura costante tra l’aria all’interno
e quella all’esterno, all’area della parete e a un coefficiente che tiene conto di tutti i
fenomeni termici.
Le resistenze termiche (reciproci dei coefficienti di scambio termico) si sommano,
mentre i coefficienti degli scambi termici danno un valore della trasmittanza inferiore al
più piccolo dei coefficienti di scambio termico.5
L’effettivo calcolo viene affidato a programmi specifici o all’applicazione di apposite
tabelle che fissano i coefficienti di scambio termico liminare e la conducibilità termica
dei materiali che compongono la parete.6
Il risultato è dunque inferiore al più piccolo dei valori ai, l lae. Per contrastare gli
effetti dovuti alla convezione e all’irraggiamento è sufficiente una parete ben
coibentata. Per esempio a Roma le nuove costruzioni, rientrando nella zona climatica
D, dove la normativa impone per la trasmittanza delle pareti il valore di 0,36 W/m 2 K ,
è sufficiente che il rapporto l l sia 0,38 W/m2 K. Se la struttura opaca verticale fosse
costituita da un unico materiale a esempio un massello in legno con l = 0,14 W/m K,
risulterebbe uno spessore di circa 37 cm. In realtà per ottenere la trasmittanza a
norma sono utilizzati materiali diversi che formano una parete multistrato, in cui è
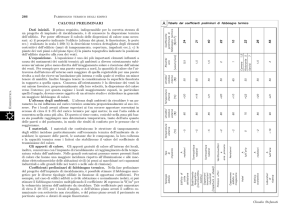
presente un isolante avente conducibilità pari a un terzo di quella del legno. Nella
scheda che segue, tratta dalle lezioni dell’Università di Pisa, la trasmittanza di 0,35
W/m2 K è ottenuta con una parete costituita da due strati di 12 cm di laterizio alveolato
(con celle contenenti aria)7 rifinite con intonaco di spessore 1,5 cm e un’intercapedine
di spessore 8 cm, con lana di roccia. Una struttura che raramente corrisponde, dal
punto di vista termico, alla stragrande maggioranza delle costruzioni romane e ancora
non sufficiente per le province più fredde d’Italia (zone climatiche E e F) che dal
gennaio 2010 devono avere costruzioni con pareti caratterizzate da trasmittanze
rispettivamente 0,34 e 0,33 W/m2 K.8 Senza parlare delle ristrutturazioni dove i valori
dovrebbero scendere a 0,27 e 0,26 W/m2 K.9
4
Spesso il simbolo utilizzato per la trasmittanza è U, ma tale lettera normalmente in termodinamica indica
l’energia interna.
5
Un risultato analogo si ha in elettrostatica con una serie di condensatori in serie. Il reciproco della
capacità complessiva è uguale alla somma dei reciproci delle singole capacità.
6
La presenza di eventuali intercapedini di aria comporta l’uso di specifiche tabelle.
7
8
Nel caso di materiale non omogeneo si parla di conduttanza e non di conducibilità.
Un utile esercizio, non difficile da realizzare a partire dagli esempi citati e dalle tabelle riportate nella
bibliografia, è calcolare la trasmittanza delle pareti del proprio appartamento o della scuola e confrontarla
con il termine 0,36 W/m2 K.
9
Un riepilogo dei valori è reperibile all’indirizzo: http://www.3therm.it/downloads/valori-trasmittanza2010.pdf