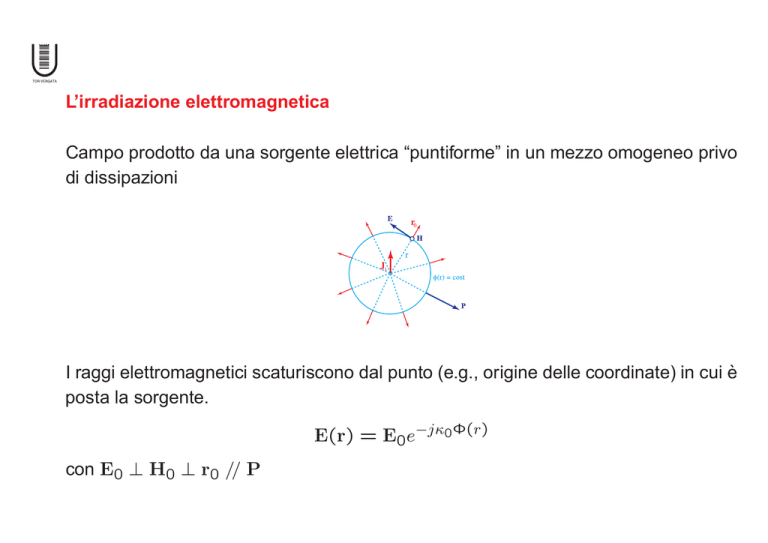
L’irradiazione elettromagnetica
Campo prodotto da una sorgente elettrica “puntiforme” in un mezzo omogeneo privo
di dissipazioni
I raggi elettromagnetici scaturiscono dal punto (e.g., origine delle coordinate) in cui è
posta la sorgente.
E(r) = E0e−jκ0Φ(r)
con E0 ⊥ H0 ⊥ r0 // P
Nel mezzo omogeneo e privo di dissipazioni, Φ(r) = n r
E(r) = E0e−jk r
e, considerata la sfera di generica superficie S centrata sulla sorgente, per la conservazione dell’energia
Re S
E × H
· n dS = Re 2
S
E0 × H0
· n dS = cost
2
∀S
E0 e H0 non possono quindi essere indipendenti dalle coordinate, ma, nell’approssi1
mazione di ottica geometrica, devono decrescere come
r
I valori iniziali di E0 e H0 dipendono inoltre dalla corrente di sorgente
Se si ricava H dalla prima equazione di Maxwell e si sostituisce nella seconda,
∇2E + k2E − ∇∇ · E = jωµJi
equazione non omogenea vettoriale che può essere risolta con l’ausilio dei potenziali
elettrodinamici
z
r0
ϕ0
θ r
θ0
J
ϕ
y
x
Assunta Ji = Jiz0 centrata sull’origine di un sistema di coordinate sferiche, se Ji è
indipendente da ϕ (simmetria assiale), anche E0 e H0 sono indipendenti da ϕ, ma
dipendono in generale da θ oltre che da r.
Definito il momento della sorgente
M = Mz0 =
Ji(r) dV
V
il campo elettromagnetico irradiato è
ηM
1
−jkr cos θ r
E =
1
+
e
0
2πr 2
jkr
1
jωµM
1
− 2 2 e−jkr sin θ θ 0
+
1+
4πr
jkr k r
jkM
1
H =
1+
e−jkr sin θ φ0
4πr
jkr
proporzionale a M
• H
– è ortogonale alla direzione della sorgente e alla direzione radiale
• E
– giace in un piano meridiano, contenente la direzione della sorgente
Le espressioni dei campi contengono somme di potenze di
1
1 λ
1
=
=
jkr
jβr
j2π r
r
λ
– possono prevalere i termini di ordine massimo o minimo
– può prevalere il componente meridiano di E rispetto a quello radiale
per cui, a seconda del rapporto
• a distanza “picola” ( rispetto a λ ) dalla sorgente
1
1
H∝ 2
E∝ 3
r
r
come nel caso statico di dipolo elettrico o magnetico
il campo nelle “vicinanze” (rispetto a λ) della sorgente è detto campo di induzione
il campo di induzione può essere elevato anche se la potenza erogata dalla
sorgente è bassa (predomina la potenza reattiva)
• a “grande” ( rispetto a λ ) distanza dalla sorgente
r0 × E
η
il campo è detto campo di radiazione e trasporta la potenza erogata (irradiata)
dalla sorgente
Ej
ηM −jβr
sin θ θ 0;
e
2λr
H
jM −jβr
sin θ φ0;
e
2λr
H=
Il campo di radiazione
• è un’onda sferica, la cui ampiezza decresce come
servazione dell’energia
1
, come richiesto dalla conr
• E e H sono trasversi tra loro e a r0 (direzione del trasporto dell’energia e direzione locale di propagazione)
• il rapporto tra E e H è l’impedenza intrinseca del mezzo
il campo asintotico ha le proprietà di un raggio elettromagnetico.
Condizioni di radiazione:
lim |rE| = cost;
r→∞
lim [r0 × η H + E] = 0;
r→∞
r→∞
r→∞
lim |rH| = cost
lim [r0 × E − η H] = 0;
Irradiazione da sorgente corta filiforme
Nel caso di sorgente cilindrica corta e sottile, con Ji indipendente dalle coordinate,
M = I
, se è la lunghezza del cilindro e I la corrente in esso.
Il campo di radiazione è
ηI e−jβr
E ∞ (r ) = j
sin θ θ 0;
2 λ r
la potenza irradiata è proporzionale a
irradia “poco”
2
λ
H∞ =
r0 × E∞
η
: se la sorgente è corta rispetto a λ, essa
per il generatore, il filamento di corrente che irradia equivale a una resistenza Ri
(resistenza di radiazione) che dissipa la potenza Wi irradiata
1
Wi =
|E∞|2 dS
2η
S
1 2π π 2 2
|E∞| r sin θ dθ dφ
Wi =
2η 0
0
1 η 2I 2 2 2π π sin2 θ 2
=
r sin θ dθ dφ
2
2η 4
λ
r
0
0
2
π
η 2 2
π
I
=
2π
sin3 θ dθ = ηI 2
8
λ
3
λ
0
2
2Wi
2
Ri = 2 = πη
I
3
λ
qualunque elemento di circuito percorso da corrente è una sorgente che irradia
c0
se λ = , la sorgente è “corta” e l’elemento di circuito irradia “poco”, ovvero
f
presenta una bassa resistenza di radiazione
per dimensioni dell’ordine del centimetro, almeno sino a frequenze dell’ordine delle
centinaia di MHz (λ 1 m), la radiazione è trascurabile e i circuiti possono essere
analizzati con le approssimazioni quasi statiche
a microonde l’effetto dell’irradiazione è apprezzabile e la teoria dei circuiti inadeguata
Le antenne
Le antenne irradiano (agiscono da sorgente) e captano il campo ettromagnetico
Parametri delle antenne
Diagramma di radiazione
Campo a grande distanza di una sorgente generica
e−jβr
E ∞ (r ) = C
f (θ, φ).
r
i primi due fattori sono gli stessi qualunque sia la sorgente
il terzo dipende da dimensioni, forma e distribuzione spaziale delle correnti ed è
quindi caratteristico dell’antenna
le proprietà radiative di un’antenna sono descritte
in ampiezza e fase dal diagramma di radiazione in campo
F(θ, φ) = rejβr E∞(r, θ, φ) = Fθ (θ, φ)θ 0 + Fφ(θ, φ)φ0
in potenza dal diagramma di radiazione in potenza
1
1
2
|F(θ, φ)|2
P (θ, φ) = r · |E∞ × H∞| =
2
2η
Il diagramma di radiazione in potenza è la densità di potenza irradiata per unità di
angolo solido (W·ster−1)
I diagrammi di radiazione dipendono dalla potenza irradiata
per avere un parametro che dipende solo dall’antenna si definisce la
Funzione di direttività:
diagramma di radiazione in potenza normalizzato alla densità angolare media di
potenza irradiata (trasmessa):
P (θ, φ)
WT
4π
La direttività di un’antenna è il valore massimo di D(θ, φ)
D(θ, φ) =
rappresentazione di D(θ, φ) in coordinate polari
Lobi
Secondari
D(θ,ϕ)
θ
Ag
ϕ
Lobo
Principale
Un’antenna opera sia in trasmissione sia in ricezione
Area equivalente
Wrp(θ, φ)
P
potenza ricevuta Wrp normalizzata alla densità superificale P di potenza incidente
Aep dipende dalla polarizzazione del campo incidente
l’area equivalente di un’antenna “ad apertura” è una frazione dell’area geometrica
Aep(θ, φ) =
Ae = ηAAg
ηA ≤ 1
ηA è il rendimento di apertura
se si riuscisse a realizzare una distribuzione di correnti impresse uniforme sull’apertura, l’area equivalente coinciderebbe con quella geometrica
in pratica, 0.5 ηA 0.8
proporzionalità tra area equivalente e direttività
λ2
Ae(θ, φ) =
D(θ, φ)
4π
Esempio di antenna ad apertura
Il collegamento radio
Due antenne A1 e A2 a distanza “grande”
A1
A2
W1
P1
W2
R
W2 = Ae2P1
P1 è la densità superficiale di potenza che A1 crea sul piano di bocca di A2
R
R
1
1
P
1
−2 0 kj (λ,s) ds
e−2 0 kj (λ,s) ds =
P1 = E1H1 = E10H10
e
2
2
R2
se
E10 e H10 sono i campi in assenza di attenuazione;
kj è l’attenuazione specifica del mezzo attraversato
D1W1 −2 R kj (λ,s) ds
0
P1 =
e
2
4πR
coefficiente di trasmissione tra le due antenne:
W2
D1 Ae2 −2 R kj (λ,s) ds
0
T12 =
=
e
2
W1
4πR
se le antenne sono ad apertura, in funzione delle aree geometriche delle antenne
Ag1 Ag2 −2 R kj (λ,s) ds
0
T12 = ηA1 ηA2
e
2
(λR)
il coefficiente di trasmissione
• cresce con le dimensioni delle antenne
• decresce con il quadrato della distanza
• cresce con la frequenza, a meno che il fattore di attenuazione, che dipende dalla
frequenza, non ne alteri la dipendenza
• non dipende dal verso di trasmissione (se il mezzo è reciproco)
Il radar
rileva la presenza di un oggetto captando una ( piccolissima ) parte della potenza
riflessa (eco radar),
determina la direzione in cui si trova (direzione di “puntamento” dell’antenna)
misura distanza (tempo intercorso tra irradiazione e captazione)
velocità radiale (spostamento Doppler)
e (sistemi sofisticati) ne identifica alcune caratteristiche (caratteristiche dell’eco)
R
Ei
WT
Ps
Wr
A
Hs
Pi
Es
Hi
quando il radar trasmette la potenza WT , sull’oggetto incide un’onda localmente piana e uniforme che trasporta una densità superficiale di potenza
DWT −2 R kj (λ,s) ds
0
Pi =
e
2
4πR
i materiali di cui è costituito l’oggetto hanno = 0 e spesso g = 0 (eventualmente
µ = µ0) per cui si ha riflessione dell’onda incidente
la potenza riflessa viene reirradiata nelle varie direzioni r0s (scattering) secondo una
funzione di reirradiazione σ(r0i, r0s) tipica dell’oggetto (forma, dimensioni, materiali)
e analoga al diagramma di radiazione in potenza di un’antenna
nella direzione r0s = −r0i è inviata una densità angolare di potenza
σ (r )P
Ps(r0i, −r0i) = b 0i i
4π
cui corrisponde una densità superficiale di potenza alla distanza R
σb(r0i)Pi −2 R kj (λ,s) ds
D WT σb −4 R kj (λ,s) ds
0
0
e
=
e
Ps =
2
2
2
4πR
(4πR )
l’antenna (di solito ricetrasmittente) A capta la potenza
2 A2 σ
ηA
Ae D σb
g b −4 R kj (λ,s) ds
−4 0R kj (λ,s) ds
0
Wr = AePs =
WT e
=
e
WT
2
2
2
4
(4πR )
4πλ R
equazione del radar
la potenza captata può essere molto bassa (RM AX 100 km, attenuazione atmosferica)
sono richiesti sistemi di ricezione sofisticati, alte potenze (anche MW), grandi antenne










