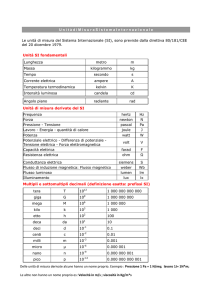
Espressione analitica esplicita del campo di induzione magnetica
generato da un anello di corrente filiforme
Graziano Donati
Nella letteratura scientifica sono note le espressioni analitiche del campo di induzione magnetica B generato da un
anello filiforme di corrente elettrica. I primi a determinare formula numeriche esplicite per un tale problema, in
coordinate rettangolari e cilindriche, sono stati M.W. Garret [1963] e Y. Chu [1998]. Espressioni analitiche implicite
sono state determinate in coordinate sferiche da David J. Jakson [1998]. In questi brevi appunti verranno presentate
delle espressioni analitiche esplicite, in coordinate rettangolari, cilindriche e sferiche del campo di induzione magnetica
B generato in un punto qualsiasi dello spazio, dovuto ad un anello filiforme di corrente elettrica planare. Il metodo quì
presentato non utilizza la legge di Biot e Savart, il cui integrale presenta un elevato grado di complessità, avendo un
termine cubico al denominatore della funzione integranda, ma utilizza il metodo del potenziale magnetico vettoriale A,
il cui calcolo è costituito da un integrale che possiede un grado di complessità di due punti inferiore, avendo un termine
lineare al denominatore della funzione integranda. Il campo B può poi essere calcolato eseguendo le derivate spaziali
del potenziale magnetico vettoriale A. Nell'esecuzione dei calcoli mi sono avvalso dell'ausilio del software
Mathematica.
Il potenziale vettoriale A è dato, come è noto dalla relazione:
2r
^2 - k 2 h K ^ k 2 h - 2E^ k 2 h
n 0 Ia
cos ^{lh
4Ia
l = n0
;
E
d
{
2
2
2
2
4r 0
4r a + r + 2ar sin ^i h
k2
a + r - 2ar sin ^i h cos ^{lh
dove r,θ e ϕ sono le usuali coordinate sferiche del punto nel quale viene calcolato il campo vettoriale A e l'argomento
degli integrali ellittici è dato da:
4ar sin ^i h
k2 = 2
a + r 2 + 2ar sin ^i h
Si noti che come argomento degli integrali ellittici è stato utilizzato k2, in linea con la convenzione di Abramowitz e
Stegun, dove m=k2. Nel caso di campo stazionario generato da corrente costante, le componenti del campo di induzione
magnetica B, possono essere ottenute, in coordinate sferiche, come:
^1 h
A{ ^ r,i h =
#
1
2 ^sin ^i h A ^ r,i hh
{
r sin ^i h 2i
2 ^ rA ^ r,i hh
Bi ^ r,i,{h = - 1r 2r
{
B{ ^ r,i,{h = 0
B r ^ r,i,{h =
Di seguito sono riportate le espressioni analitiche delle componenti del campo. Per semplicità, utilizziamo le seguenti
sostituzioni di variabile:
a2 = a 2 + r 2 - 2ar sin ^i h
b2 = a 2 + r 2 + 2ar sin ^i h
2
k2 = 1 - a 2
b
n0 I
C= r
Componenti del campo
Componenti del campo
Derivate spaziali delle componenti del campo
Derivate spaziali delle componenti del campo
COORDINATE CARTESIANE
Di seguito sono riportate le componenti del campo e le loro
derivate in coordinate cartesiane. Queste espressioni sono più
semplici da utilizzare nel caso si rendano necessarie operazioni
di traslazione e di rotazione, non dovendo eseguire
trasformazione dei versori di base. Per semplicità,
consideriamo le seguenti sostituzioni di variabile
a2 = a 2 + r 2 - 2at
b2 = a 2 + r 2 + 2t
2
k2 = 1 - a 2
y 2 = x2 - y 2
b
n0 I
C= r
COORDINATE CILINDRICHE
- 2at
= a + t + z consideriamo
a semplicità
Per
le seguenti sostituzioni
2
2
2
2
b = a + t + z 2 + 2at
2
k2 = 1 - a 2
b
n0 I
C= r
2
2
2
Componenti del campo
Componenti del campo
Conclusioni
Derivate spaziali delle componenti del campo
Sono state presentate delle semplici espressioni in forma
chiusa che per il calcolo del campo di induzione
magnetica B generato, in un punto qualsiasi dello spazio,
da un anello filare di corrente elettrica. Nonostante queste
formule siano esatte, esse richiedono la valutazione
numerica di integrali ellittici. Esistono altri metodi per il
calcolo del campo B, ad esempio mediante sviluppo in
serie [3] o mediante valutazione numerica con metodo
degli elementi finiti [6]. Tuttavia, questi metodi soffrono
di limitazioni dovute agli errori di arrotondamento. Il
metodo qui mostrato aggira queste limitazioni ed è
limitato solo dalle capacità di calcolo degli integrali
ellittici. L'inclusione delle espressioni delle derivate
spaziali del campo B, può trovare importanti applicazioni
del campo della magnetoidrodinamica e della fisica dei
plasmi.
Bibliografia
Casi limite
Per completezza, seguono le espressioni di alcuni
casi limite
Lungo l'asse della spira
Vicino all'asse della spira (x,y <<a)