RETTE PARALLELE
DEF: Due rette r,s si dicono parallele se non hanno nessun punto in comune o se coincidono ( s ≡ r )
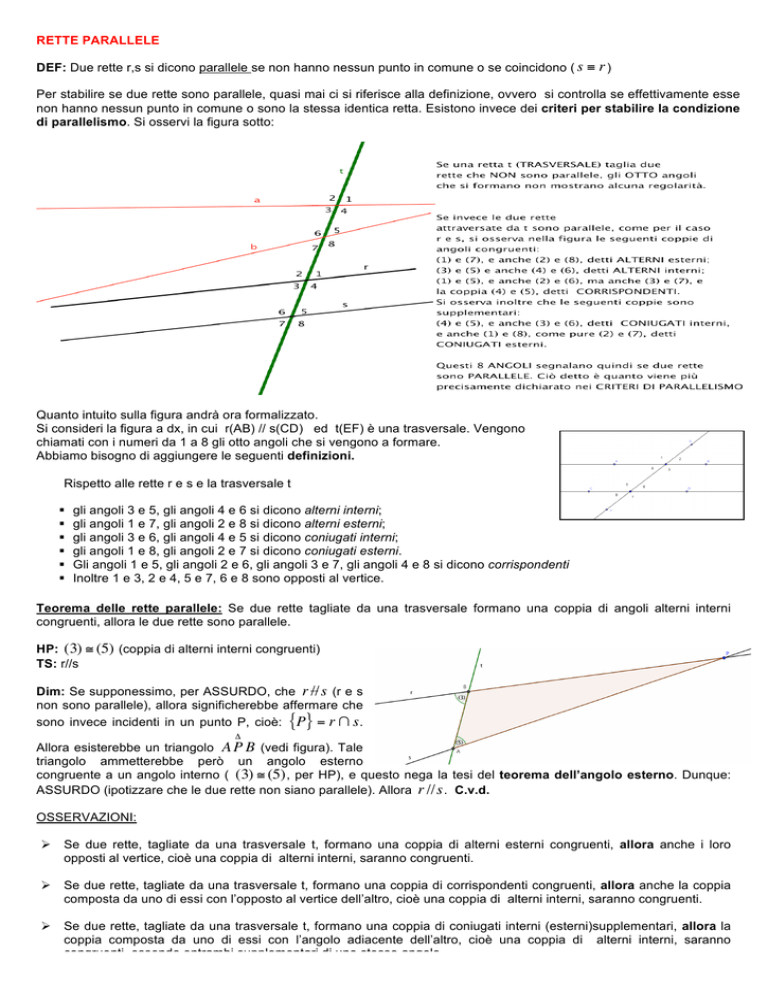
Per stabilire se due rette sono parallele, quasi mai ci si riferisce alla definizione, ovvero si controlla se effettivamente esse
non hanno nessun punto in comune o sono la stessa identica retta. Esistono invece dei criteri per stabilire la condizione
di parallelismo. Si osservi la figura sotto:
€
Quanto intuito sulla figura andrà ora formalizzato.
Si consideri la figura a dx, in cui r(AB) // s(CD) ed t(EF) è una trasversale. Vengono
chiamati con i numeri da 1 a 8 gli otto angoli che si vengono a formare.
Abbiamo bisogno di aggiungere le seguenti definizioni.
Rispetto alle rette r e s e la trasversale t
gli angoli 3 e 5, gli angoli 4 e 6 si dicono alterni interni;
gli angoli 1 e 7, gli angoli 2 e 8 si dicono alterni esterni;
gli angoli 3 e 6, gli angoli 4 e 5 si dicono coniugati interni;
gli angoli 1 e 8, gli angoli 2 e 7 si dicono coniugati esterni.
Gli angoli 1 e 5, gli angoli 2 e 6, gli angoli 3 e 7, gli angoli 4 e 8 si dicono corrispondenti
Inoltre 1 e 3, 2 e 4, 5 e 7, 6 e 8 sono opposti al vertice.
Teorema delle rette parallele: Se due rette tagliate da una trasversale formano una coppia di angoli alterni interni
congruenti, allora le due rette sono parallele.
HP: (3) ≅ (5) (coppia di alterni interni congruenti)
TS: r//s
€
Dim: Se supponessimo, per ASSURDO, che r // s (r e s
non sono parallele), allora significherebbe affermare che
sono invece incidenti in un punto P, cioè: {P} = r ∩ s .
Δ
Allora esisterebbe un triangolo A P€B (vedi figura). Tale
triangolo ammetterebbe però un angolo esterno
congruente a un angolo interno ( (3) ≅ (5) , per HP), e questo nega la tesi del teorema dell’angolo esterno. Dunque:
ASSURDO (ipotizzare che le due€
rette non siano parallele). Allora r //s . C.v.d.
OSSERVAZIONI:
€
€
Se due rette, tagliate da una trasversale t, formano
€ una coppia di alterni esterni congruenti, allora anche i loro
opposti al vertice, cioè una coppia di alterni interni, saranno congruenti.
Se due rette, tagliate da una trasversale t, formano una coppia di corrispondenti congruenti, allora anche la coppia
composta da uno di essi con l’opposto al vertice dell’altro, cioè una coppia di alterni interni, saranno congruenti.
Se due rette, tagliate da una trasversale t, formano una coppia di coniugati interni (esterni)supplementari, allora la
coppia composta da uno di essi con l’angolo adiacente dell’altro, cioè una coppia di alterni interni, saranno
congruenti, essendo entrambi supplementari di uno stesso angolo.
€
€
Il Teorema precedente può essere ampliato con altri casi, e prende il nome di:
Teorema: Criteri di parallelismo. Se due rette r, s, tagliate da una trasversale t, formano :
una coppia di angoli alterni interni o esterni congruenti, OPPURE
una coppia di angoli coniugati interni o esterni congruenti, OPPURE
una coppia di corrispondenti supplementari
allora le due rette r,s sono parallele.
Una conseguenza importante:
Corollario: Se due rette r,s, sono perpendicolari ad una stessa retta t,
allora r//s.
Dato un punto P e una retta r, abbiamo già stabilito che esiste ed è unica la retta p perpendicolare ad r e passante per P.
Ora ci si chiede se esiste, ed è unica, una retta parallela alla retta assegnata r e passante per P.
Si può costruire per P una retta parallela alla retta r : basta costruire una retta t
passante per P e un punto di r, quindi costruire una retta per P che formi insieme
a r e t angoli alterni interni congruenti. Tuttavia non si riesce a dimostrarne
l’UNICITA’. Storicamente, i geometri hanno invano cercato la dimostrazione dell’
unicità della retta parallela, e nell’attesa hanno deciso di accettarne il fatto
come ASSIOMA (cioè come ovvio.) Tale famoso assioma ha un nome:
Quinto postulato di Euclide: Dati una retta r e un punto
Si può dimostrare che vale anche il Teorema inverso delle rette parallele: Se r//s, allora tagliate da una trasversale t
formano coppie di alterni interni congruenti.
Allora, tutto quanto discusso fin qui sul parallelismo
€ si sintetizza nel seguente
Teorema: Due rette nel piano sono parallele
⇔
tagliate da una trasversale, formano:
1. angoli alterni interni o alterni esterni congruenti, oppure
2. angoli corrispondenti congruenti, oppure
3. angoli coniugati interni o coniugati esterni supplementari.
Alcune conseguenze:
€
Noto che r//s, allora valgono tutte e tre le relazioni (1), (2) e (3); pertanto si potranno usare nelle dimostrazioni di altri fatti.
Corollario: Se r //s e t⊥r ⇒ t⊥s .
Corollario: Se r //s e s //q ⇒ r //q . (proprietà transitiva del parallelismo)
Corollario: Se a e b sono incidenti e a //r e b //s ⇒ r e s sono pure incidenti.
€
€NEI POLIGONI
GLI ANGOLI
€
€
II Teorema dell’angolo esterno:
In un
€
€ triangolo, ciascun angolo esterno
è congruente alla somma dei due angoli interni non adiacenti.
HP: ABC triangolo
TS:
Cˆ e = Aˆ + Bˆ
Dim: Tracciando la retta r per C e parallela a AB si ha:
1.
BCˆ r ≅ Bˆ (alterni interni formati da AB//r e la trasversale BC)
2.
rCˆ C'≅ Aˆ (corrispondenti formati da AB//r e la trasversale AC’)
3.
Cˆ e = BCˆ r + rCˆ C'
€
€
P ∉ r , è unica la retta passante per P e parallela a r.
€
Cˆ e ≅ Aˆ + Bˆ
c.v.d.
CONSEGUENZE:
ˆ = Cˆ + Cˆ e = Cˆ + Aˆ + Bˆ ).
In un triangolo, la somma degli angoli interni è congruente ad una angolo piatto (infatti: p
In un triangolo rettangolo, i due angoli acuti sono complementari.
Un triangolo equilatero, dunque equiangolo, ha tutti tre gli angoli congruenti alla terza parte dell’angolo piatto (60°).
€
In un poligono convesso di n lati:
(1) la somma degli angoli interni è congruente a
(n − 2) pˆ .
(2) la somma degli angoli esterni è congruente a un
angolo giro. (Dimostrare!!!)
€
CRITERI DI CONGRUENZA NEI TRIANGOLI RETTANGOLI
I tre CCT studiati per i triangoli in generale, applicati al caso di una coppia di triangoli rettangoli vedono ridotte le condizioni
( da tre a due) per la loro applicabilità: la terza condizione è sottintesa e consiste nel fatto che due triangoli rettangoli
hanno per loro definizione già un angolo congruente, l’angolo retto. Osservare la figura sotto.
Valgono quindi i seguenti criteri:
I CCTR (Criterio di Congruenza dei Triangoli Rettangoli): Se due triangoli rettangoli hanno i due cateti congruenti, allora
sono congruenti.
II CCTR (Criterio di Congruenza dei Triangoli Rettangoli): Se due triangoli rettangoli hanno un cateto e un angolo acuto
corrispondenti congruenti, allora sono congruenti.
III CCTR (Criterio di Congruenza dei Triangoli Rettangoli): Se due triangoli rettangoli hanno l’ipotenusa e un angolo
acuto, allora sono congruenti
Inoltre vale anche:
IV CCTR (Criterio di Congruenza dei Triangoli Rettangoli): Se due triangoli rettangoli hanno l’ipotenusa e un cateto
congruenti, allora sono congruenti.
€
€
€
Δ
Δ
Δ
Δ
HP:
A B C e A' B'C' rettangoli in A
BC ≅ B'C'
AC ≅ A'C'
TS:
A B C ≅ A' B'C'
Dim: Si costruisca il triangolo A1’B1’C1’, congruente a A’B’C’, tale che:
A1’C1’=AC (segmenti che coincidono perfettamente). Come rappresentato
nella figura a lato, si vede che si ottiene un triangolo B1BC isoscele sulla
Bˆ ' 1 ≅ Bˆ ' per cos truzione
ˆ '≅ Bˆ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯⎯→ Bˆ '≅ Bˆ . E anche Cˆ ≅ Cˆ ' (per
base B1’B; allora B
1
ˆ ). Ora si
differenza di angoli: la somma degli angoli interni in un triangolo è p
può applicare, ad esempio, il ICCT ai triangoli ABC e A’B’C’ (essi hanno
l’ipotenusa e gli angoli adiacenti rispettivamente congruenti) e si può
€
affermare che
Δ
Δ
A B C ≅ A' B'C' c.v.d.
€
€
In sintesi:
Due triangoli sono congruenti se hanno congruenti, oltre all’angolo retto, altri due elementi di cui uno almeno è
€
un angolo.










