152
Capitolo 5. Onde e particelle
g(k0 ) = (A2 x21 /2π); al crescere di |k0 − k| il valore di g 2 (k) decresce
rapidamente.
La trattazione svolta si basa su un modello piuttosto artificioso. I
risultati ottenuti svolgono una funzione puramente illustrativa:
¦ se si assume che gli atomi emettano onde monocromatiche di
pulsazione ω0 = 2πν0 (vettore d’onda k0 = 2π/λ 0 ) per un intervallo di tempo finito τ , si ottiene che, in realtà, gli atomi
emettono un pacchetto d’onda costituito dalla sovrapposizione
di infinite onde la cui pulsazione ω è ‘centrata’ sulla frequenza
ω0 e la cui ampiezza decresce rapidamente al crescere di |ω0 − ω|;
¦ un’onda rigorosamente monocromatica deve avere un’estensione
spaziale infinita.
5.4
Larghezza naturale di una riga
Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico
di pulsazione ω0 ; la carica, essendo accelerata, emette onde elettromagnetiche e perde quindi energia. Il suo moto è pertanto un moto
armonico smorzato descritto dall’equazione:
ẍ = −ω02 x − 2γ ẋ
dove ω0 è la pulsazione del moto in assenza di smorzamento. Nel caso
in cui lo smorzamento è debole - γ ¿ ω0 - la soluzione diventa:
x = x0 e−γt cos(ωs t + δ)
con
(5.2)
q
ωs =
ω02 − γ 2
e con la costante di fase δ arbitraria. La (5.2) descrive un moto armonico di pulsazione ωs la cui ampiezza decresce esponenzialmente in funzione del tempo. Si noti che la pulsazione del moto smorzato è minore
5.4 Larghezza naturale di una riga
153
di quella del moto non smorzato. Tuttavia, essendo γ ¿ ω0 , è possibile porre ωs = ω0 . Nell’approssimazione in cui γ ¿ ω0 , l’accelerazione
della particella è quindi data da:
a = −ω02 x
Sotto le condizioni del punto B) di pagina 130, il campo elettrico generato a distanze sufficientemente grandi dalla particella è proporzionale
alla sua accelerazione ritardata. Tra queste condizioni, ricordiamo qui
quella relativa alla velocità v della particella: v ¿ c.
⇒ Se una particella si muove di moto armonico con pulsazione ω (x = x0 sin ωt), la sua velocità quadratica media
è data da:
K
ω 2 x20
2
vrms
=
< ẋ2 >=
m
2
dove K è la costantepdi forza del moto ed m la massa
della particella (ω = K/m). Pertanto:
1
vrms = ωx0
2
Per una lunghezza d’onda λ = 600 nm, ω = 3.14×1015 rad
s−1 . Ne segue che vrms = 3.14 × 105 ms−1 ¿ c, se si pone
x0 = 0.2 nm.
Pertanto, il campo elettrico dell’onda generata dalla particella in moto
armonico smorzato può essere espresso dalla formula:
E(t) = 0
per
t<0
E(t) = E0 e
−γt iω0 t
(5.3)
e
per
t≥0
La trasformata di Fourier della funzione E(t) è (si veda l’equazione
4.19):
1 Z +∞
E(t)e−iωt dt
E(ω) = √
2π −∞
154
Capitolo 5. Onde e particelle
Quindi, per la (5.3):
Z +∞
1
E(ω) = √ E0
E(t)e−[i(ω−ω0 )+γ] dt
0
2π
Pertanto:
1
γ − i(ω − ω0 )
E(ω) = √ E0 2
2π γ + (ω − ω0 )2
Questa espressione rappresenta il valore del campo elettrico per unità
di pulsazione dovuto alla componente di pulsazione ω; il campo elettrico dovuto alle componenti comprese in un intervallo ∆ω sufficientemente piccolo (rispetto all’intervallo minimo in cui E(ω) varia in modo
significativo) è quindi dato da (equazioni 4.20 e 4.22):
∆E = E∆ωeiωt
L’energia associata a questo campo, data dal vettore di Poynting
mediato su un periodo, è:
∆I =
∆ω 2
E02 ε0
4π γ 2 + (ω − ω0 )2
(5.4)
In corrispondenza di ω = ω0 si ha il massimo di intensità:
∆I0 =
E02 ε0
∆ω 2
4πγ 2
Pertanto la (5.4) può essere scritta sotto la forma:
∆I = ∆I0
γ2
γ 2 + (ω − ω0 )2
La funzione:
f (ω − ω0 ) =
γ2
γ 2 + (ω − ω0 )2
(5.5)
(5.6)
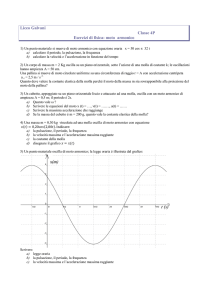
detta lorentziana, è mostrata in figura 5.7. L’intensità ∆I è uguale
alla metà di ∆I0 per
ω − ω0 = ∆ω = γ
5.4 Larghezza naturale di una riga
155
1
0.9
0.8
0.6
0
f(ω−ω )
0.7
0.5
0.4
0.3
0.2
0.1
0
−10
−5
0
ω−ω0 (108 rad s−1)
5
10
Figura 5.7: andamento della lorentziana dell’equazione (5.6).
γ è quindi la semi - larghezza della funzione f (ω − ω0 ) a metà altezza.
La larghezza intera della riga a metà altezza è quindi uguale a 2γ.
Il risultato espresso dalla (5.5) coincide con quello della fisica quantica. Alla luce della fisica quantica, i presupposti del modello classico
sono errati perché:
¦ si suppone che l’emissione di radiazione elettromagnetica sia
dovuta al moto armonico di particelle elettricamente cariche;
¦ si suppone che l’emissione di energia sia un processo continuo.
La ragione per cui, ciò non ostante, il modello classico produce lo stesso
risultato della fisica quantica risiede nel fatto che esso prevede che
la carica oscillante perda energia secondo una legge esponenziale del
tipo e−2γt ; questa legge, se si pone τ = 1/2γ, è la legge di decadimento
quantico di un numero statisticamente significativo di atomi eccitati la
cui vita media sia τ . La descrizione classica ‘funziona’ in questo caso,
ma è complessivamente inadeguata per la descrizione dei fenomeni del
mondo microscopico.
La forma delle righe di emissione osservate sperimentalmente non
è una lorentziana. Ciò è dovuto al fatto che ci sono altre due cause
156
Capitolo 5. Onde e particelle
di allargamento delle righe: i processi d’urto e l’effetto Doppler. Se la
sorgente luminosa è costituita da un gas o un vapore, le sue molecole
(o i suoi atomi) subiscono degli urti: se si suppone che una molecola
eccitata emetta un fotone in seguito ad un urto, la legge che descrive
la perdita di energia da parte delle molecole eccitate è ancora del tipo
e−t/τc , dove τc indica l’intervallo di tempo medio tra due urti consecutivi. Ne consegue che l’allargamento della riga dovuto alle collisioni
è ancora di tipo lorentziano: siccome, tuttavia, τc è, in generale, più
piccolo di τ , l’allargamento dovuto alle collisioni predomina rispetto a
quello ‘intrinseco’, responsabile della larghezza naturale della riga.
⇒ Il libero cammino medio l delle molecole di un gas è
espresso dalla relazione:
1
< l >= √
2πd2 n
dove d è il diametro delle molecole e n la loro concentrazione. D’altra parte, la velocità media di una molecola è
data da:
s
8kT
< v >=
πm
dove k è la costante di Boltzmann, T la temperatura assoluta e m la massa delle molecole. Ricordando che, quando
V = 1, per la legge dei gas perfetti:
p
n=
kT
dove p è la pressione, si ottiene per il vapore di mercurio
a T = 300 K e ad una pressione p = 0.1 atm:
< l > = 4.09 × 10−6 m
< v > = 177.95 ms−1
τc = 2.3 × 10−8 s
In questo caso, l’intervallo di tempo medio tra due urti
successivi τc è dello stesso ordine di grandezza di τ .
L’allargamento della riga dovuto all’effetto Doppler verrà discusso
nella sezione 5.11 a pagina 203.