momento angolare

Dinamica dei corpi in rotazione
Sono le leggi che governano il moto dei corpi in rotazione.
Non sono nuove leggi fisiche, ma derivano dalle tre leggi di
Newton, a volte con derivazioni matematiche complesse che
eviteremo.
Supponiamo che la palla sia
mantenuta in rotazione, essa è
caratterizzata dalle grandezze
r, w e la sua velocità v = w r
La sua quantità di moto sarà:
Q = mv = m·r·w
Se si vuole incrementare la sua
velocità, devo applicare una forza;
supponiamo che al sasso sia applicata
una forza tangente alla traiettoria per
un certo tempo Dt.
Essa fa aumentare la velocità angolare
di Dw
DQ = m r Dw
F Dt = DQ = m r Dw
Momento angolare: corpo
puntiforme
r
P
O
Il momento angolare per un corpo
puntiforme P di massa m che si
muove di moto circolare uniforme
con velocità v secondo una
circonferenza di raggio r e centro in
O ha una definizione molto semplice
L = mv  r
V
Unità di misura: Kg∙m2/s
Momento angolare
Poiché il prodotto m∙v è la quantità di
moto Q, il momento angolare può
anche essere definito in questo
modo:
r
O
L = Qr
P
V
L = Q b
Momento angolare
oppure, poiché la velocità lineare v è
legata alla velocità angolare ω dalla
relazione:
v =wr
r
P
V
O
Il momento angolare può essere
anche così scritto:
L = m  r w
2
Momento di inerzia
La quantità:
I = mr
2
Viene definita MOMENTO DI INERZIA di un punto
materiale rispetto al centro O della traiettoria. Con questa
posizione il momento angolare può anche sinteticamente
essere così scritto:
L = I w
Momento angolare e quantità di
moto
Da notare l’analogia formale tra quantità di moto e
momento angolare, entrambe date dal prodotto di una
velocità (quella lineare nel primo caso, quella angolare nel
secondo) per una grandezza legata alla massa del corpo
Q = mv
L = I w
Questa analogia formale si traduce in una analogia tra le
leggi che presiedono alla variazione di tali grandezze
Energia cinetica
Anche l’energia cinetica può essere espressa in termini di
momento di inerzia e velocità angolare, infatti:
1
2
Ec = m  v
2
1
2
2
Ec = m  r  w
2
I = mr
2
v =wr
1
2
Ec = I  w
2
Energia cinetica
Questa espressione dell’energia cinetica in termini del
momento di inerzia e della velocità angolare non è molto
interessante nella trattazione del corpo puntiforme ma lo
diventa nel caso del corpo rigido
1
2
Ec = I  w
2
Vettore momento angolare
L
r
P
V
O
Così come la quantità di moto,
anche il momento angolare è in
realtà un vettore.
Il vettore L è perpendicolare al
piano di rotazione del corpo, e il
suo verso è dato dal pollice della
mano destra, tenuto
perpendicolare al palmo, quando
le altre dita ruotano
accompagnando la rotazione del
corpo
Definizione generale: raggio vettore
O
r
P
Si dice RAGGIO VETTORE di un
punto P rispetto al punto O (polo) il
vettore che unisce il punto O con il
punto P
Il verso del raggio vettore è quello
che va da O a P
Definizione generale: momento
angolare
O
L
Si dice MOMENTO ANGOLARE
del punto materiale P rispetto al
polo O il prodotto vettoriale del
raggio vettore per la quantità di
moto del corpo Q
r
 
L = r Q
P
V
Definizione generale: momento
angolare
O
L
r
P
V
Naturalmente, nel caso del moto
circolare uniforme, la definizione
generale si riduce a quella
particolare
L = Qr
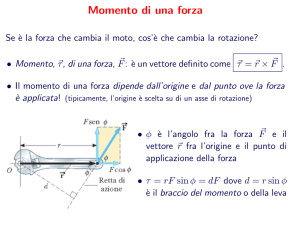
Momento di una forza
Il momento di una forza rispetto a
un fulcro O è il prodotto della forza
F per il braccio b, ovvero la
distanza tra il fulcro e la retta del
vettore forza
b
O
F
M = F b
Momento di una forza: definizione
generale
Il momento di una forza rispetto a
un fulcro O è il prodotto vettoriale
del raggio vettore che unisce il
fulcro al punto di applicazione della
forza e il vettore forza stesso
z
O
r
y
F
M
x
  
M = r F
Variazione del momento angolare
Se un corpo è soggetto a una forza F per un tempo t, la
variazione della quantità di moto del corpo è regolata
dalla seconda legge di Newton:
DQ = F  Dt
Analogamente, la variazione del momento angolare di un
corpo soggetto a una forza di momento angolare M per un
tempo t è:
 
DL = M  Dt
Cenno alla dimostrazione
Questa legge è un teorema.
La dimostrazione è semplice nel caso del moto circolare,
infatti in questo caso vi sono diverse semplificazioni:
• le grandezze sono semplici scalari e non vettori
• il momento angolare è semplicemente Q∙r
• la forza agente è perpendicolare al raggio della curva
(infatti una componente radiale verrebbe annullata dalla
reazione vincolare)
• il braccio è uguale al raggio, quindi il momento della forza
è semplicemente F∙r
Cenno alla dimostrazione
L = Qr
O
r
F
M = F r
Cenno alla dimostrazione
Partendo dalla seconda legge di Newton:
DQ = F  Dt
Si moltiplicano entrambi i membri per r
r  DQ = r  F  Dt
Poiché r è costante può essere portato dentro al segno di Δ
D(r  Q) = r  F  Dt
E sostituendo secondo quanto visto nella precedente
diapositiva si ha la tesi
DL = M  Dt
Conservazione del momento
angolare
Il momento angolare è una delle grandezze meccaniche
soggette a conservazione
In un sistema isolato il momento angolare
totale è costante
Per momento angolare totale si intende, naturalmente, la
somma dei momenti angolari di tutti i corpi facenti parte del
sistema
Momento angolare: corpo rigido
Un corpo rigido è un corpo esteso (ovvero che occupa un
volume non nullo) e la cui forma non può subire nessuna
modifica. I corpi solidi sono in prima approssimazione corpi
rigidi.
Per prima cosa prenderemo in considerazione un corpo
rigido rotante intorno a un asse fisso a, come una ruota, con
una data velocità angolare ω
Momento angolare: corpo rigido
r
a
Il corpo può essere diviso in un
insieme di piccole particelle,
ognuna delle quali possa essere
considerata un corpo puntiforme.
Ognuna di queste particelle
descrive una circonferenza di
raggio r intorno all’asse di
rotazione e ha un suo momento
angolare dato dalla formula nota:
l = m  r w
2
Momento angolare: corpo rigido
r
a
Da notare che è stata usata, tra
le diverse varianti, la formula che
contiene la velocità angolare:
infatti tutte le particelle che
formano il corpo hanno la stessa
velocità angolare, ma diverse
velocità lineari
l = m  r w
2
Momento angolare: corpo rigido
r
Si dice momento angolare del
corpo rigido rispetto all’asse a la
somma di tutti i momenti angolari
delle particelle che lo
compongono
L =  mi  ri  w
2
a
Momento di inerzia
Poiché ω è una costante possiamo metterla in evidenza e
porla fuori dal simbolo di sommatoria
L=
 mi  ri w
La quantità:
I=
2
 mi  ri 
2
Viene detta MOMENTO DI INERZIA del corpo rispetto
all’asse a
Momento angolare e energia
cinetica
Il momento angolare del corpo rigido rotante intorno a un
asse fisso può quindi essere scritto nella stessa forma di
quello del corpo puntiforme
L = I w
Allo stesso modo l’energia cinetica
1
2
Ec = I  w
2
Momento angolare: verso
L
a
Per quanto riguarda il verso
ci si regola esattamente
come per la particella
puntiforme:
Il verso del vettore momento
angolare è quello del pollice
della mano destra quando le
altre dita della mano girano
seguendo la rotazione del
corpo
Significato del momento di inerzia
Così come la massa può essere considerata come la
misura della tendenza di un corpo a mantenere il suo stato
di quiete o moto rettilineo uniforme (infatti maggiore è la
massa, più è difficile modificare il moto) il momento di
inerzia può essere considerato come la misura della
tendenza di un corpo a mantenere il suo stato di moto
circolare uniforme: maggiore è il momento di inerzia, più
sarà difficile modificare il moto rotatorio del corpo
Volano
Nel motore a scoppio sull’albero
motore viene applicato un
volano, ovvero un disco di
elevato momento di inerzia: lo
scopo è quello di stabilizzare il
moto rotatorio dell’albero stesso,
che altrimenti andrebbe a scatti e
tenderebbe ad arrestarsi
Momenti di inerzia a confronto
Il momento di inerzia non dipende solo dalla massa ma,
come si nota dalla formula, anche da come essa è
distribuita intorno all’asse di rotazione:
• se la massa è concentrata intorno all’asse di rotazione r
sarà piccolo e quindi I sarà piccolo
• se la massa è concentrata lontano dall’asse di rotazione r
sarà grande quindi I sarà grande
I=
 mi  ri 
2
Momenti di inerzia a confronto
Ad esempio, a parità
di massa un anello
avrà un momento di
inerzia maggiore di
un disco, perché la
sua massa è
concentrata
soprattutto alla
periferia, quindi
lontano dall’asse di
rotazione
Effetto pattinatore
Quando un pattinatore sta
ruotando su se stesso può
variare la sua velocità angolare
allargando o stringendo gli arti:
• aprendo gli arti il momento di
inerzia aumenta perché la massa
è distribuita più lontano dall’asse
di rotazione
• stringendo gli arti il momento di
inerzia diminuisce perché la
massa è più concentrata intorno
all’asse di rotazione
Effetto pattinatore
Per il principio di conservazione
del momento angolare:
• quando il momento di inerzia
aumenta la velocità angolare
diminuisce
• quando il momento di inerzia
diminuisce la velocità angolare
aumenta
L = I w
Effetto pattinatore
Lo stesso effetto è utilizzato
anche nei tuffi e nella danza
Collasso gravitazionale
Durante il collasso gravitazionale
di una stella che ha esaurito il
suo combustibile nucleare il
momento di inerzia diminuisce,
perché la massa si concentra
verso il centro, e quindi la
velocità angolare aumenta.
Le stelle di neutroni, ultima fase
del collasso per stelle di massa
non troppo grande, ruotano su
se stesse molto rapidamente
Collasso gravitazionale
Il momento angolare posseduto dal sole e dai pianeti del
sistema solare è quello che aveva la nebulosa originaria.
La velocità di rotazione doveva essere all’inizio molto
piccola, ma man mano che le masse si concentravano
diveniva sempre più grande
Momento di inerzia dei corpi
Come si nota dalla formula il momento di inerzia non
dipende solo dalla forma del corpo ma anche dall’asse di
rotazione: per ogni asse di rotazione esiste un diverso
momento di inerzia, per cui i momenti di inerzia di un corpo
sono infiniti.
E’ però possibile dimostrare che per ogni corpo rigido
esistono tre assi, detti assi principali di inerzia, e che tutti i
momenti di inerzia relativi a qualsiasi altro asse sono una
combinazione dei momenti di inerzia relativi ai tre assi
principali
Momento di inerzia dei corpi
Giroscopio
Si dice giroscopio un corpo
rigido (solitamente un disco)
libero di ruotare nello spazio.
Nella pratica il disco deve
essere montato su un
supporto: perché il disco sia
libero di ruotare si adotta un
particolare montaggio che
prende il nome di
sospensione cardanica
Giroscopio
L
Per la conservazione del
momento angolare, quando
un giroscopio viene orientato
verso una direzione, ad
esempio verso la stella
polare, esso tende a
mantenere fissa questa
direzione anche quando viene
spostato in altri punti
Bussola giroscopica
Questo effetto oggi è utilizzato
per sostituire le bussole
magnetiche (che non indicano
il nord geografico, ma quello
magnetico) con le più efficienti
bussole giroscopiche
Moto di precessione
Quando un giroscopio viene
sottoposto ad una forza
avente un dato momento,
l’effetto è quello di spostare
l’asse di rotazione in direzione
del momento torcente stesso
L
M
Moto di precessione
Infatti, per la legge del moto:
ΔL
 
DL = M  t
L
L’
M
Come si vede dal disegno, se
si aggiunge al vettore L il
vettore ΔL si ottiene un nuovo
vettore L’, che rappresenta il
momento angolare
modificato, spostato nella
direzione di M
Moto di precessione
Se questo avviene in
modo continuo, anche il
vettore momento
angolare, e quindi l’asse
di rotazione si spostano
di continuo, e ciò
provoca un moto detto
di precessione.
Nel moto di precessione
la punta del vettore L
descrive un cono
Trottola
ΔL
L
r
M
O
F=mg
Questo moto lo si osserva
nella trottola: la forza che
genera il momento torcente è
la forza peso, il punto O è il
punto di contatto della trottola
col piano di appoggio,
supposto fisso a causa della
reazione vincolare, il raggio
vettore va da O al baricentro
della trottola
Ruota
M
L
ΔL
r
O
F=mg
Lo stesso effetto si
ha quando una
ruota rotola sul
terreno: la stabilità
giroscopica
impedisce che la
ruota cada (come
succederebbe se la
ruota fosse ferma)
facendo invece
curvare la
traiettoria (infatti la
ruota nel suo
percorso procede
sempre perpendicolarmente al
vettore L)
Precessione degli equinozi
ΔL
L
M
La Terra può essere
considerata un grande
giroscopio. A causa del suo
rigonfiamento equatoriale
le forze combinate di sole e
luna producono una forza
di momento non nullo che
provoca un moto di
precessione dell’asse di
rotazione, proprio come
una trottola
Precessione degli equinozi
ΔL
L
M
Questo fa sì che nel corso
dei secoli l’asse di
rotazione non sia volto
verso lo stesso punto della
volta celeste e che i punti
di intersezione tra il piano
di rotazione e quello di
rivoluzione (che
corrispondono agli
equinozi) si spostino nella
fascia dello zodiaco con un
periodo di circa 25.800
anni
Moto traslatorio e rotatorio
Fino ad ora sono stati
studiati separatamente il
moto di un corpo
puntiforme nello spazio
(moto di traslazione) e la
rotazione di un corpo
esteso intorno a un asse
fisso.
In realtà di solito anche i
corpi estesi, oltre al moto
rotatorio, compiono un
moto traslatorio, come ad
esempio la Terra
Moto traslatorio e rotatorio
Nella Terra separiamo il
moto traslatorio che la
Terra compie intorno al
sole in un anno (moto di
rivoluzione) da quello di
rotazione della Terra
intorno al proprio asse in
un giorno (moto di
rotazione)
Moto traslatorio e rotatorio
In realtà questo è sempre possibile; il moto di un corpo
rigido può essere separato in:
• Moto traslatorio del baricentro, equivalente a quello di un
punto materiale, con massa pari alla massa del corpo, una
data velocità v, e regolato dalla legge:
 
Dp = F  t
• Moto rotatorio, equivalente a quello di un corpo rigido
intorno a un asse passante per il baricentro, con momento
di inerzia dato I e, una data velocità angolare ω, regolato
dalla legge:
 
DL = M  t
Moto traslatorio e rotatorio
Un esempio è dato dal
moto della ruota di
un’automobile:
V
V
ω
• il centro della ruota
trasla parallelamente al
terreno con velocità pari
a quella dell’automobile
• la ruota gira intorno a
tale centro con moto
circolare
Moto traslatorio e rotatorio
V
ω
E’ da notare che in questo caso moto
rotatorio e traslatorio sono sincronizzati.
Infatti, in assenza di slittamento il punto
della ruota a contatto col terreno è fermo,
quindi è necessario che la velocità
periferica di rotazione della ruota sia
uguale e contraria a quella di traslazione.
Se R è il raggio della ruota tra velocità di
traslazione e velocità angolare sussiste
pertanto la relazione:
v =wR
Terra e luna
Anche il moto di rotazione
della luna su se stessa è
sincronizzato con quello
di rivoluzione intorno alla
Terra, per cui la luna
rivolge sempre la stessa
faccia alla Terra.
Ciò è dovuto a una
complessa interazione
gravitazionale che ha
trasferito energia e
momento angolare tra
Terra e luna.
Terra e sole
Al contrario, il moto di
rotazione della Terra su
se stessa non è
sincronizzato con quello
di rivoluzione intorno al
sole perché le forze
agenti sono risultate
troppo deboli
Moto traslatorio e rotatorio
Il momento angolare complessivo del corpo può essere
separato in due componenti:
• Momento angolare del punto materiale, dovuto al moto
traslatorio rispetto a un polo O
• Momento angolare intrinseco, dovuto alla rotazione del
corpo rigido intorno all’asse di rotazione
Moto traslatorio e rotatorio
Nella fisica atomica e subatomica queste due componenti
hanno un nome particolare:
• Il momento angolare dovuto alla traslazione della particella
(ad esempio la rotazione di un elettrone intorno al nucleo
atomico) si chiama momento angolare orbitale
• Il momento angolare intrinseco dovuto alla rotazione della
particella su se stessa si chiama spin
Energia cinetica
Anche l’energia cinetica può essere separata in due
componenti:
• Quella dovuta alla traslazione del punto materiale, detta
energia cinetica traslazionale
• Quella dovuta alla rotazione del corpo rigido su se stesso,
detta energia cinetica rotazionale
Energia cinetica
L’energia cinetica di un corpo rigido può quindi essere
scritta in questa forma:
1
2 1
2
Ec = m  v  I  w
2
2
Dove v è la velocità di traslazione del punto materiale e ω la
velocità angolare di rotazione del corpo rigido intorno
all’asse
Lo yoyo
Lo yoyo fornisce un semplice
esempio di come l’energia
cinetica in un corpo rigido si
suddivide tra traslazionale e
rotazionale.
Se si lascia cadere lo yoyo come
se fosse un sasso l’energia
potenziale della forza peso si
trasforma in energia cinetica
traslazionale, come in caduta
libera
Lo yoyo
Se invece lo yoyo viene lasciato
tenendo la cordicella, l’attrito della
corda mette in rotazione il disco e
l’energia potenziale si trasforma in
gran parte in energia cinetica
rotazionale, per cui lo yoyo
scende più lentamente
aumentando progressivamente la
velocità di rotazione
Lo yoyo
Quando lo yoyo giunge a fine
corsa, sempre grazie al filo la
rotazione si inverte e il disco
comincia a risalire man mano che
l’energia cinetica rotazionale si
ritrasforma in energia potenziale
(salvo la parte persa per attrito)