Capitolo 1
Supernovae
1.1
Generalita
Nello studio di ogni fenomeno sico un ruolo preliminare ed importante e rivestito dalla
analisi delle tipologie attraverso cui il fenomeno si manifesta e dal tentativo che segue
di raggruppare i fenomeni in classi signicative. Questo vale evidentemente anche per le
Supernovae (SNe), eventi in cui una stella diviene per qualche mese piu brillante della
intera galassia che la ospita. Per le SNe esistono tuttavia, due diÆcolta non facilmente
superabili che riguardano la casualita del fenomeno e la scarsita di eventi vicini, facilmente
osservabili, per i quali si possano derivare dati completi ed aÆdabili.
Da quando e nata l'astronomia moderna, evento che si puo far coincidere con l'introduzione
e l'uso di strumentazione per misure oggettive di tipo sia spettroscopico sia fotometrico
(quindi sicuramente non prima del XX secolo) non si e osservata nessuna supernova galattica. Peraltro, e plausibile ritenere che dall'ultimo evento registrato nel 1604 altre SNe
possano essere esplose nella Galassia, il fenomeno restando totalmente oscurato dal gas e
dalla polvere presenti nel disco galattico.
La quasi totalita delle nozioni ad oggi acquisite sul fenomeno derivano quindi da osservazioni di SNe in galassie esterne spesso anche molto lontane. Esistono stime, piu o meno
aÆdabili, riguardanti la luminosita massima raggiunta da tre eventi avvenuti in epoca
storica nella nostra galassia, ed identicati successivamente come supernovae, registrati
rispettivamente nel 1054, nel 1572 e nel 1604. Delle ultime due esiste anche una stima
della luminosita in tempi successivi a quelli del massimo di emissione luminosa.
La comparsa improvvisa di stelle \nuove" molto luminose, di breve durata, nettamente
distinte dalle comete, era nota n dall'antichita. Non stupisce pertanto che l'idea che
esistesse una classe di fenomeni esplosivi ben piu energetici delle piu comuni \novae" si fece
strada con una certa lentezza. Gia nel 1919 Lundmark aveva intuito che potessero esserci
eventi distinti dalle \novae" ordinarie per il fatto di avere una luminosita al massimo
molto piu elevata, si deve tuttavia a Baade e Zwicky, nel 1934, la formalizzazione del
1
2
Capitolo 1. Supernovae
concetto che esistessero fenomeni esplosivi che superano di diversi ordini di grandezza
l'energia emessa durante l'esplosione di una \nova" comune. Si deve anche agli stessi
autori la coniazione del termine \supernova". Un ruolo determinante nel processo di
chiaricazione lo ebbero quattro supernovae vericatesi tra il 1884 ed il 1930 in alcune
galassie vicine (M31,IC 4182, NGC5223 ed NGC 4214), e, tra queste, in modo particolare
S-andromedae, la supernova del 1884 nella vicina galassia di Andromeda (M 31) che
peraltro fu a lungo considerata una nova comune. Anche l'analisi dei dati di Tyco Brahe
concernenti la supernova galattica del 1572, che oggi porta il suo nome, fu decisiva nel
consentire nel 1933 a Baade e Zwicky di prendere la decisione sopre citata, apparsa in
stampa l'anno seguente.
Nel 1936 Zwicky diede inizio alla prima campagna osservativa sistematica dedicata
alla ricerca di supernovae in galassie vicine. Da questa survey, che si concluse nel 1939,
scatur il primo tentativo di classicazione per le Supernovae. Quando nel 1965, stendendo il suo contributo al volume VIII di Stars and Stellar Systems, Zwicky si trovo a
dover sintetizzare i risultati della sua lunga esperienza di ricerca nel settore, esord dicendo
che l'esistenza delle Supernovae, come eventi distinti dalle novae comuni, fu chiaramente
capita dopo diversi decenni di coscienziosa ricerca. Gia negli anni quaranta era peraltro
consolidata la convinzione che i due fenomeni, di nova e supernova, fossero totalmente
distinti e che potessero aver origine del tutto diversa. Nell'autorevole volume di Cecchini
e Gratton "Le stelle Nuove" edito dalla Hoepli nel 1942 si legge: "Il termine stella nuova
e adoperato, in generale, per indicare una stella che da uno splendore normale, pressoche costante, sale improvvisamente ad uno splendore enormemente piu grande e poi,
nel corso di qualche anno ritorna, spesso con uttuazioni secondarie, allo splendore primitivo. Questa denizione comprende un certo numero di oggetti che, al massimo splendore,
hanno una grandezza assoluta intorno a -7 e che si osservano indierentemente nella Via
Lattea e nelle nebulose a spirale piu vicine, e forse un numero ristretto di oggetti che,
al massimo raggiungono una grandezza assoluta intorno a -14; questi ultimi sono stati
osservati nelle nebulose estragalattiche e, probabilmente, anche nella Via Lattea. Noi chiameremo, come di consueto, nuove comuni, o semplicemente nuove, gli oggetti della prima
categoria e supernuove quelli piu luminosi". Cecchini e Gratton nel loro volume, dedicato
essenzialmente alle novae, riportano anche le curve di luce di sei supernovae identicate
con certezza in galassie prossime alla nostra.
Fino al 1987, anno della famosa supernova 1987A nella vicina galassia Grande Nube
di Magellano, satellite della nostra Galassia, erano state osservate, con piu o meno accuratezza, circa 150 supernovae extragalattiche. 1987A, vericatasi nel febbraio del 1987,
fu la prima a poter essere osservata ad occhio nudo dopo quasi quattrocento anni. Si
nota che le supernovae vengono catalogate con una sigla che contiene l'anno in cui si
vericano seguito da una lettera dell'alfabeto che, a partire dalla lettera A, ne identica
la successione temporale della scoperta.
1.1.
Generalita
3
Fig. 1.1: Curve di luce schematiche nel Blu per i tipi piu rappresentativi di Supernovae secondo Cappellaro
et. al 1997 (Cortesia di Enrico Cappellaro).
Fig. 1.2: Aspetto spettroscopico di tre supernovae tipiche appartenenti ciascuna ad uno dei tipi piu
rappresentativi secondo Cappellaro et. al 1997. Le righe piu signicative di ciascuno spettro sono state
indicate esplicitamente (cortesia di Enrico Cappellaro)
4
Capitolo 1. Supernovae
1.2 Classicazione e Curve di Luce
I criteri di classicazione delle supernovae si fondano su dati osservativi ottenuti dalle
tecniche fotometriche e da quelle spettroscopiche. Facendo uso delle prime e possibile
determinare quella che viene denita curva di luce che riporta l'andamento temporale della
luminosita in una banda ssata. Generalmente vengono utilizzate la magnitudine nella
banda visuale (V) e quella nella banda blu (B). Quando e possibile si utilizzano anche altre
bande fotometriche. Se si giunge cos a coprire l'intero spettro della radiazione emessa e
possibile ricavare la curva di luce bolometrica, ovvero l'andamento della luminosita totale
in funzione del tempo, grandezza molto rilevante nel confronto tra teoria ed osservazioni.
Le osservazioni spettroscopiche, oltre a permettere l'identicazione degli elementi
chimici presenti nel materiale espulso, consentono di misurare le velocita dello stesso, e
di derivare l'energia meccanica associata all'evento ove si abbiano indicazioni sulla massa
coinvolta nel fenomeno.
Il primo e piu importante criterio di classicazione divide le supernovae in due tipi a
seconda che negli spettri compaiano o meno le righe dell'idrogeno. Se negli spettri della
supernova non compaiono mai le righe dell'idrogeno questa viene denita di tipo \uno"
o SN I. Nel caso contrario, in cui le righe dell'idrogeno dominino gli spettri, la supernova
viene denita di tipo \due" o SN II.
All'interno dei due gruppi si e trovato opportuno eettuare una ulteriore sottoclassicazione. Le supernovae di tipo II sono state divise in tipoII-P e tipo II-L, dove P ed
L indicano, rispettivamente, Plateau e Lineare. Questa suddivisione viene fatta in base
alle caratteristiche della curva di luce nel visuale. Dogget e Branch (1985) suggeriscono i
seguenti andamenti nel blu e nel visuale:
SN II-P : in banda V presentano un massimo esteso della durata di circa ottanta giorni
e poi una discesa a due pendenze. Nel blu (banda B) il massimo di luminosita e seguito
da una discesa quasi continua interrotta da un plateau tra i quaranta e gli ottanta giorni
dopo il massimo.
SN II-L : presentano, sia nel blu che nel visuale, una discesa post-massimo, continua
a due pendenze.
La possibilita e/o l'opportunita di operare una suddivisione semplicemente dicotomica
puo, tuttavia, non essere generalmente condivisa. Le curve di luce delle supernovae di
tipo II sono mediamente eterogenee e non e facile denirne delle curve di luce medie che le
dividano in un numero chiaro di sottoclassi. Questa proprieta ha trovato conferma nel caso
della SN 1987A che ha presentato un andamento molto al di fuori di quelli comunemente
osservati. Ad ogni modo, accettando che la maggioranza delle SNe II sia inquadrabile nei
tipi P ed L, si ha che la frequenza statistica delle II-L sembra risultare inferiore a quella
delle tipo II-P. In una rianalisi di curve di luce di supernovae classicate II-L e II-P di
cui era ragionevolmente nota la distanza si e concluso, ([3]), che le SNe II-L appaiono piu
omogenee tra di loro sia per quanto riguarda la luminosita di picco sia per la curva di luce
1.3. Supernovae e Popolazioni Stellari.
5
post-massimo (magnitudini assolute nel blu al massimo di luminosita comprese tra -16.5
e -18). Le SNe II-P mostrano una piu spiccata disomogeneita (magnitudini assolute nel
blu al massimo comprese tra -14 e -20).
Recentemente, e stato necessario operare delle suddivisioni anche all'interno della
classe I che veniva precedentemente considerata sostanzialmente omogenea. Infatti, un
certo numero di SNe che, in virtu dell'assenza totale di idrogeno dagli spettri devono essere
classicate per denizione di tipo I, hanno mostrato di possedere spiccate peculiarita sia
spettroscopiche sia nella curva di luce tali da separarle dalla classe di SNe riconosciuta da
tempo come di tipo I ed ora denominate di tipo Ia o tipo I classiche. Le SNe appartenenti
alla nuova classe sono state denite come di tipo Ib ma anche come tipo I sottoluminoso,
tipo I peculiare o, inne, di tipo I radioemittente.
Le curve di luce delle supernovae di tipo Ia costituiscono un insieme decisamente
piu omogeneo di quelle di tipo II, pertanto, per le tipo Ia e denibile con una discreta
aÆdabilita una curva di luce media. Tuttavia, appare accertato che anche all'interno della
classe delle SN Ia non sia percorribile l'ipotesi di totale omogeneita. La curva di luce delle
SNe di tipo Ia presenta, sia nel blu che nel visuale, un andamento post-massimo di tipo
lineare a due pendenze. Tenendo presente che la magnitudine costituisce una espressione
logaritmica del usso energetico, tale tipo di decadimento e, in realta, di tipo esponenziale
a due indici. Le magnitudini visuali assolute al massimo assumono valori dell'ordine di
MV 18:5 19.
Le supernovae di tipo Ib si dierenziano dalle Ia per diversi aspetti osservativi:
1) sono sottoluminose, rispetto alle Ia, di circa due magnitudini visuali,
2) presentano spesso una emissione radio che compare molto presto e che declina molto
rapidamente,
3) la popolazione stellare di appartenenza dei progenitori stellari sembra dierente da
quella delle tipo Ia ed appare essere piu prossima a quella delle supernovae di tipo II,
4) presentano sempre la riga a 5876 A(He I), che non appare mai nelle tipo Ia nelle
quali invece esiste quella del Si II a 6355 A(shiftata a 6100 A).
Piu recentemente e stata anche suggerita una ulteriore sottoclassicazione delle SN I
identicando un tipo denito Ic. Non e ancora chiaro se tra le Ib e le Ic esista un certo
grado di continuita.
1.3 Supernovae e Popolazioni Stellari.
In galassie ellittiche si sono nora osservate solo supernovae di tipo Ia. Nelle galassie a
spirale, si osservano tutti i tipi di SNe: SNe II, SNe Ib/c e SNe Ia.
6
Capitolo 1. Supernovae
SUPERNOVAE
Fenomeni che producono una luminosit
a migliaia di volte maggiore
di quella della galassia in cui avvengono (Lundmark, 1920)
SNe Ia
Presentano la riga
di assorbimento
a = 6150A
SNe Tipo I
SNe Tipo II
Assenza delle righe di Balmer
Presenza delle righe di Balmer
nello spettro ottico
nello spettro ottico
SNe Ib
Non presentano la riga
di assorbimento
a = 6150A
Presentano una forte
riga a = 5876A
SNe Ic
Non presentano la riga
di assorbimento
a = 6150A
Non presentano una forte
riga a = 5876A
Esplodono nelle regioni H II (Stelle massicce)
SNe II L
La curva di luce
presenta un esteso
plateau al massimo
SNe II P
La curva di luce
presenta una
decrescita lineare
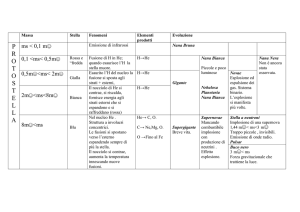
Tab. 1.1: Schema di classicazione delle supernovae in relazione al loro spettro.
Nelle galassie a spirale si osserva che le supernovae di tipo II e di tipo Ib/c tendono a
presentarsi in prossimita dei rami di spirale o in zone dove e attiva la formazione stellare,
mentre le supernovae di tipo Ia appaiono piu uniformemente distribuite su tutto il disco.
Tenendo presente che nelle galassie ellittiche non sembra esserci formazione stellare in atto
e che appare ragionevole supporre che questa deve essersi esaurita diversi miliardi di anni
addietro, la citata topologia delle SNe suggerisce un primo quadro, molto preliminare,
delle proprieta evolutive dei progenitori stellari dei vari tipi di supernovae. Le supernovae
di tipo II e di tipo Ib devono discendere da progenitori stellari a rapida evoluzione mentre i
progenitori delle supernovae di tipo Ia devono avere tempi tempi evolutivi di spettro molto
ampio, da pochi milioni no a diversi miliardi di anni. Puo apparire ragionevole tentare
una identicazione dei progenitori delle supernovae di tipo II (e forse delle tipo Ib/c) con
stelle di massa medio-alta mentre non e immediata una identicazione dei progenitori
delle supernovae di tipo Ia.
L'idea che stelle massicce ad evoluzione rapida fossero alla base delle SNe II e di
vecchia formulazione ed ha resistito, invariata negli anni, no a trovare brillante conferma
a seguito della SN 1987A, per la quale e stato possibile risalire inequivocabilmente al
progenitore attraverso immagini del campo stellare precedenti l'evento esplosivo. Invece,
l'iter per l'identicazione dei progenitori delle supernovae di tipo Ia e stato notevolmente
travagliato ed una soluzione generalmente accettata non e ancora stata raggiunta (si veda
il capitolo successivo).
Va sottolineato il fatto che l'associare le supernovae di tipo I con la popolazione stellare
1.4. Supernovae storiche e frequenza delle esplosioni.
7
II e le SN II con la popolazione I, come viene talora fatto, puo generare confusione.
Innanzitutto e molto probabile (se non addirittura certo) che molte delle SNe I osservate
nelle galassie a spirale siano originate dalla pop I di disco. Inoltre, le SNe I osservate
nelle galassie ellittiche traggono origine da una popolazione che e paragonabile alla nostra
pop II in termini di eta ma molto piu simile alla nostra pop I dal punto di vista delle
abbondanze metalliche.
I concetti storici di popolazione stellare sviluppati per la nostra galassia perdono infatti
parte del loro signicato se estesi al di fuori della nostra galassia. Le osservazioni hanno
ormai consentito di conoscere nel dettglio altri sistemi stellari in cui l'evoluzione ha seguito
strade dierenti da quelle della Galassia. All'esistenza ormai accettata, di popolazioni
stellari che, seppure vecchie, sono molto ricche di metalli (galassie ellittiche o i bulges delle
galassie a spirale), si aÆancano popolazioni stellari giovani ricche di stelle massicce ma
poco abbondanti di elementi pesanti (per es. sistemi simili alle Nubi di Magellano), cade
cioe la correlazione metallicita - eta che e alla base della classicazione delle popolazioni
stellari della Galassia.
In virtu di quanto detto, la popolazione di appartenenza delle varie supernovae va
considerata da caso a caso. Un aspetto che apparira evidente nel seguito, quando verranno
esaminate le storie evolutive dei progenitori stellari dei vari tipi di supernova.
1.4 Supernovae storiche e frequenza delle esplosioni.
Negli ultimi duemila anni, e prima dell'inizio della moderna ricerca sistematica, nella
nostra galassia si sono vericati un certo numero di eventi, di cui si ha traccia storica,
e che sono stati successivamente identicati come eventi di supernova. Degli ultimi due
(1572 e 1604) si possiede, come si e gia accennato, una documentazione estesa e, rispetto
alle possibilita osservative del periodo, esauriente. Piu scarsa e la documentazione relativa ad eventi riportati per gli anni 185, 393, 1006, 1054 e 1181. Dell'ultimo non esiste
traccia negli annali europei e solo recentemente e stata rintracciata documentazione occidentale relativa alla SN del 1054 ([5]). Questo fatto, apparentemente sorprendente, e
stato giusticato, a nostro avviso con un po' di fatica, con la radicata credenza aristotelica
sull'immutabilita dei cieli di cui gli europei continuanvano ad essere portatori nel medio
evo. Si deve alle trascrizioni di due monasteri (Santa Soa di Benevento e San Gallo
in Svizzera) l'esistenza delle uniche registrazioni europee della supernova del 1006 che,
seppur relativamente bassa sull'orizzonte, fu di splendore tale da eguagliare quasi la luna
piena (il cielo ne era rischiarato ed alla sua luce, in notte priva di luna, si potevano vedere
gli oggetti). Particolarmente brillante fu anche la supernova del 1054, al punto da poter
8
Capitolo 1. Supernovae
essere vista anche di giorno. La documentazione occidentale rinvenuta recentemente sulla
SN del 1054 ([5]) porta informazioni complementari a quelle della precedente documentazione storica di origine cinese e giapponese e sembra aiutare a circostanziare meglio
l'evoluzione temporale di quella supernova. L'argomento relativo alle supernovae storiche
e stato trattato ampiamente da Clark e Stephenson nel libro "The Historical Supernovae"
e, in forma piu concisa, in un articolo apparso su Scienze (1986, N. 98, Vol XVII, pg. 82).
I valori stimati della magnitudine massima apparente delle supernove storiche sono,in ordine temporale da quella del Centauro del 185 a quella di Keplero: -8, -1, -9, -5, 0, -4, e
-3.
E possibile usare i dati relativi alle supernovae storiche per fare una banale stima,
necessariamente molto imprecisa, sulla frequenza con cui si vericano eventi di supernova nella nostra Galassia. Attraverso una stima delle distanze si ottiene che le supernovae storiche sono tutte localizzate approssimativamente sul piano galattico. Questo non
stupisce in modo particolare, quello che in un primo momento stupisce, e che esse si localizzano in un'area di disco costituita da un settore circolare relativamente piccolo (circa
una sessantina di gradi) dove e contenuto anche il Sole. Il motivo di tale distribuzione
e ragionevolmente semplice e risiede nel fatto che le supernovae piu distanti non sono
state osservate a causa dell'assorbimento determinato dalla materia interstellare che giace
sul piano galattico (polveri e gas). Si puo cos stimare che per ogni sei supernovae nella
nostra galassia se ne e osservata, in media, solo una. La media galattica potrebbe quindi
aggirarsi intorno a circa una supernova ogni 80 anni. La media locale di osservabilita
nell'ottico risulterebbe di una supernova ogni circa 300 anni. Un'analisi piu realistica
sulla probabilita con cui si vericano gli eventi di supernova in un ssato sistema stellare
richiede peraltro un campione molto esteso di galassie esterne.
Viene sovente usata come unita di misura della frequenza di supernovae l'SNu (SuperNova units). Si tratta di una unita specica di frequenza: 1 SNu equivale ad un tasso
di una supernova ogni 100 anni ogni 1010 luminosita solari nel blu del sistema stellare
che ospita la supernova. Annotiamo che se la necessita di denire un tasso specico appare evidente, la scelta di normalizzare rispetto alla luminosita e sicamente fondata e
corrisponde ad un requisito di praticita mentre la scelta storica della banda blu potrebbe
invece risultare piu discutibile.
Esistono diversi lavori di campionatura estesa (temporalmente e spazialmente) di
eventi di supernova in galassie esterne. Tra questi ricorderemo quello di Asiago iniziato da
Leonida Rosino nel 1959 e proseguito successivamente dai suoi collaboratori ed un altro
condotto da Evans dal 1980. Recentemente, Cappellaro ed altri ([1]) hanno rianalizzato i
risultati di 5 diversi esperimenti di ricerca di SNe con lo scopo di fornire tassi aÆdabili ed
errori di misura quanto piu ridotti possibile. I risultati di questo lavoro sono sintetizzabili
come segue. Per galassie spirale di tipo Sbc-Sd si stimano i seguenti tassi:
1.5. Aspetti generali delle Supernovae in (astro-)Fisica.
9
SNe tipo Ia : 0.24 0.09 SNu
SNe tipo Ib/c: 0.16 0.08 SNu
SNe tipo II : 0.88 0.37 SNu
Per galassie di tipo S0a-Sb i tassi risultano invece:
SNe tipo Ia : 0.20 0.07 SNu
SNe tipo Ib/c: 0.11 0.06 SNu
SNe tipo II : 0.40 0.19 SNu
Inne, per galassie ellittiche si ha:
SNe tipo Ia : 0.15 0.06 SNu
avendo stimato le distanze attraverso un valore della costante di Hubble di 75Kms 1 Mpc 1 .
Questi risultati sono estendibili con qualche cautela alla nostra galassia, presumibilmente intermedia tra tipo Scd e tipo Sd, per la quale si avrebbe un tasso di SNe di tutti
i tipi di circa 1.3 SNu. Tuttavia, le stime della luminosita assoluta nel blu della nostra
galassia sono alquanto imprecise ed oscillano tra circa 1:6 e 4:0 1010 L;B . Questi
valori conducono ad una stima di un tasso galattico di SNe che va dai 2 ai 6 eventi di
qualsiasi tipo ogni 100 anni, forse eccessivamente elevato rispetto a quello dedotto dalle
supernovae storiche.
1.5 Aspetti generali delle Supernovae in (astro-)Fisica.
Dall'analisi fotometrica e spettroscopica di un evento di supernova e possibile ricavare
indicazioni sulla quantita di energia emessa sotto forma di energia cinetica del materiale
espulso e sotto forma di emissione di onde elettromagnetiche.
Si trova che in un'esplosione di supernova vengono liberati, nelle forme energetiche
citate, circa 1051 erg, con dierenze non sostanziali tra i vari tipi di supernova. Talvonta
si trova usata in letteratrura l'unita di misura energetica \foe"; 1 foe corrisponde a 1051 erg
(fifty one erg). Esistono in natura almeno due meccanismi in grado di generare energie
di quest' ordine di grandezza in tempi trascurabili. Il primo fu indicato gia nel 1933,
quando Zwichy, subito dopo la scoperta dell'esistenza del neutrone da parte di Chadwick
10
Capitolo 1. Supernovae
(1932), intu che se una stella normale fosse collassata in una stella di neutroni si sarebbero
liberati 1053 erg a spese dell'energia gravitazionale: piu dell'energia di legame tipica
di una stella ( 1048 erg ), piu energia di quanta il Sole sia in grado di liberarne durante
l'intero corso della sua vita ( 1051 erg ). Questa intuizione ha retto brillantemente agli
sviluppi delle successive ricerche no a trovare conferma sperimentale in occasione della
SN 1987A, quando la dierenza tra l'energia totale prevista e quella osservata (cinetica
piu e.m.) e stata eettivamente rivelata sotto forma di neutrini.
Un secondo meccanismo, identicato piu recentemente, consiste nella possibilita di estrarre l'energia richiesta esclusivamente da combustioni nucleari. L'innesco dalla reazione
di termofusione del carbonio, 12 C +12 C , in condizioni di pesante degenerazione elettronica comporta uno sviluppo indiscriminato delle termofusioni successive che non si arresta
no a quando la materia non sia stata tutta trasformata in elementi del picco del ferro.
In questo processo viene liberata nell'arco di qualche secondo un'energia di 1051 erg
per ogni massa solare di materia bruciata. Esistono in realta altri meccanismi di origine
nucleare in grado di produrre energie dell'ordine del foe, uno di questi verra discusso piu
avanti.
Le supernovae (SNe) rappresentano in ogni caso l'evento evolutivo nale di stelle che,
seppure con modalita e tempi talvolta profondamente diversi, riescono ad innescare tutte
le reazioni nucleari avanzate no al bruciamento del silicio compreso. Nell'evento di SN
viene espulsa nello spazio interstellare una frazione rilevante della stella progenitrice della
quale rimane al piu un oggetto stellare iperdenso di massa relativamente bassa. In taluni
casi l'intero progenitore stellare viene totalmente distrutto dall'esplosione. In poco tempo
(giorni) la stella progenitrice diviene piu brillante della galassia cui appartiene e gli eetti
dell'esplosione rimangono osservabili per mesi su tutto lo spettro elettromagnetico con
aspetti ed accentuazioni che assumono un andamento temporale complesso e variegato
che dipende dal tipo di evento esplosivo e dalle proprieta del progenitore stellare.
Le condizioni siche estreme in cui si trova la materia nelle fasi pre-esplosive, i fenomeni
che determinano l'istaurarsi dell'evento esplosivo ed la sua evoluzione dinamica nonche le
interazioni che guidano l'evoluzione successiva della componente espulsa e di quella collassata, rendono sicuramente importante (oltre che aascinante) lo studio delle supernovae
in diversi ambiti della sica e dell'astrosica.
Tuttavia, l'interesse per lo studio delle SNe non si esaurisce di certo in questi soli aspetti
in quanto:
i) la parte espulsa contiene materia profondamente rielaborata dalle combustioni nucleari
avvenute sia durante le fasi esplosive sia durante le precedenti fasi evolutive quiescenti.
Questa materia, ricca di elementi pesanti, dopo un processo di diluizione con il mezzo
interstellare, andra a formare altre stelle o, eventualmente, pianeti. Il materiale espulso
1.5. Aspetti generali delle Supernovae in (astro-)Fisica.
11
possiede suÆciente energia per "spazzare" il gas interstellare in quiete, per comprimerlo
e per indurre in questo formazione di nuove stelle. Si viene cos ad iterare un processo
ciclico, di nascita e morte stellare, che contiene in se i principi base dell'evoluzione chimiconucleare della materia nelle galassie: piu sono temporalmente avanzate le generazioni stellari di una galassia, piu le stelle in formazione saranno ricche di elio e di elementi pesanti
a discapito di un minore contenuto percentuale di idrogeno. E importante ricordare che al
momento della nascita di una generazione stellare, oltre a stelle di alta massa, che evolveranno rapidamente ed esploderanno presto come supernovae iterando il ciclo, si formano
stelle di massa bassa, i cui tempi di vita sono superiori a quello dell'universo. Queste stelle
restano a testimoniare, per tempi estremamente lunghi, le condizioni chimiche della materia all'atto della formazione: vengono conservate informazioni che, una volta decifrate,
consentono di ripercorrere la storia dell'evoluzione chimica della materia nella galassia e
delle continue modiche che l'esplosione delle SNe, o altre fonti di inquinamento, inducono
in essa.
ii) Le SNe immettono nel gas intergalattico un quantitativo di energia i cui eetti nel
produrre fuoriuscita di materia diusa dalla buca di energia potenziale della galassia non
possono essere ignorati. E d'altronde noto che l'eÆcienza della formazione stellare dipende
anche dalla densita della materia diusa, pertanto appare chiaro come le SNe costituiscano
un meccanismo di regolazione dell'evoluzione galattica in termini di capacita e rapidita
di formazione stellare e di arricchimento di materia ad alto numero atomico.
iii) Un ulteriore motivo che determina l'importanza delle SNe in sica consiste nel fatto
che alcuni tipi di queste producono un usso di neutrini particolarmente rilevante; se
l'esplosione e avvenuta nella nostra galassia, i rivelatori di neutrini attualmente in funzione
consentono una accurata registrazione l'evento. La decodica dell'informazione portata
dai neutrini si rivela di primaria importanza sia per la determinazione delle condizioni
siche sul luogo dell'esplosione sia per la stessa conoscenza della sica dei neutrini.
iv) Ci si aspetta, inoltre, che gli stessi tipi di SNe che producono un evento neutrinico
importante, liberino anche una parte rilevante di energia sotto forma di onde gravitazionali. Questi tipi di SNe costituiscono l'unico "generatore" di onde gravitazionali in grado
di produrre un segnale rivelabile dalle attuali antenne gravitazionali. Queste antenne
dovrebbero gia oggi essere in grado di rivelare un segnale se l'esplosione avviene nella
nostra galassia o in una molto prossima ad essa. La prossima generazione di antenne
gravitazionali sara presumibilmente in grado di registrare segnali anche da supernove
distanti qualche mega-parsec.
v) Ci sono alcune classi di supernovae che presentano delle proprieta osservative dotate
di un certo grado interno di omogeneita come, ad esempio, nel massimo di luminosita e
nel suo andamento temporale cos come nell'aspetto dello spettro. Qeste supernovae costituiscono, pertanto, un potente mezzo di calibrazione delle distanze; tanto piu che, data
12
Capitolo 1. Supernovae
la loro elevata luminosita intrinseca, esse sono utilizzabili per misure su scale di distanze
per le quali gli altri indicatori primari di distanza sono ormai divenuti inutilizzabili.
vi) Le SNe costituiscono sicuramente un test per le teorie dell'evoluzione stellare. Questo
vale in particolare per l'evoluzione in caso di binarieta dove, come si vedra nel capitolo
successivo, diverse fenomenologie attendono ancora di essere chiarite (e non solo nei dettagli).
Inne, quei tipi di supernova che derivano da progenitori stellari a rapida evoluzione ci
indicano i siti dove la formazione stellare e attiva ed il viceversa consente di imporre limiti per stabilire quando la formazione stellare deve essere cessata; e stato suggerito che
le supernovae possano essere i produttori dei raggi cosmici o che esse costituiscano un
sito privilegiato dove questi vengono accellerati; le SNe producono elementi radioattivi
a tempo di decadimento lungo che emettono fotoni X e quindi possono essere parte attiva nella produzione del fondo X osservato (esempio tipico quello legato al problema del
decadimento dell'alluminio 26); i resti compatti lasciati dall'esplosione delle SNe a progenitore massiccio possono essere determinanti nel formare la cos detta materia oscura
d'importanza nello studio della dinamica delle galassie, degli ammassi di galassie ed in
cosmologia.
La varieta e vastita di temi in cui le SNe intervengono giustica gli sforzi attualmente
in corso per risolvere i problemi ancora aperti che precludono una piena comprensione del
fenomeno.
1.6 SUPERNOVAE A COLLASSO GRAVITAZIONALE
Una stella di massa superiore a circa 12M presenta, nel corso della sua evoluzione, condizioni siche centrali tali da consentire l'innesco quiescente di tutte le reazioni nucleari
esoenergetiche che seguono quella di bruciamento dell'idrogeno. Questo signica che durante tutto il corso della vita della stella non si sono manifestate condizioni di pesante
degenerazione elettronica.
Il susseguirsi di reazioni nucleari che interessano nuclei successivamente piu pesanti,
ha termine quando viene superato il limite naturale per il quale una reazione nucleare
di fusione costituisce un guadagno energetico netto. Come e noto, detto limite si manifesta quando le reazioni interessano materia i cui nuclei hanno il numero atomico del
Ferro. Piu appropriatamente, al termine della cobustione del silicio, l'ultima a costituire
un guadagno energetico netto, la materia si presenta in un insieme di nuclei con numero
atomico distribuito intorno a quello del ferro. In questo stato evolutivo la materia stellare
raggiunge quello che viene denito equilibrio statistico nucleare (NSE), la cui composizione
viene genericamente indicata con \Fe". La distribuzione di equlibrio della materia in NSE
non dipende dalle sezioni d'urto ma dall'energia dei nuclei ed e descritta da un'equazione
1.6. SUPERNOVAE A COLLASSO GRAVITAZIONALE
13
tipo Saha. In questo stato, ad un aumento di temperatura non segue, come di norma
avviene, una maggiore produzione di energia termonucleare bens un assorbimento destinato a fare transitare una data distribuzione di NSE in una piu energetica. Pertanto una
distribuzione di NSE e denita a partire dai suoi parametri termodinamici.
Esaurito il combustibile centrale, il bruciamento del Si si sposta in una shell progressivamente piu esterna. Si viene cos a creare un core di \Fe" (o in NSE) la cui massa
e destinata a crescere. E signicativo notare che quando il bruciamento del Silicio si e
spostato in una shell abbastanza esterna (MSi;shell 1M ), temperatura e densita centrali assumono rispettivamente valori dell'ordine di Tc 1010 K e c 1010 gr cm 3
(per stelle di massa medio-alta: 20 25M ). In queste condizioni i vari contributi alla
pressione sono dati, rispettivamente, da:
Pi 2 1026 dyne cm
2
(1.1)
Pe 1028 dyne cm 2
(1.2)
dove Pi e Pe sono le pressione dovuta agli ioni e quella dovuta agli elettroni. Il contributo
della pressione di radiazione e ancora piu basso e risulta essere
Prad 3 1025 dyne cm 2
(1.3)
Pertanto, il contributo piu importante alla pressione proviene dagli elettroni.
D'altra parte, dagli assegnati valori di T e , da cui segue un valore del parametro di
degenerazione 10, e facile derivare che si e in presenza di materia i cui elettroni sono
degeneri e relativistici. E noto, peraltro, che esiste un limite superiore alla massa che
una struttura degenere relativistica puo assumere senza che la gravita prevalga (limite
di Chandrasekhar). Tale limite (a temperatura zero) e esprimibile attraverso la seguente
relazione:
MCh = 5:83(Ye)2 M
(1.4)
Dove Ye e il numero di elettroni liberi per barione. Per l'idrogeno Ye e uguale ad 1,
mentre per la materia piu evoluta Ye assume valori che, a partire da 0.5, vanno sempre
piu diminuendo all'aumentare del livello di neutronizzazione della materia.
Quando la massa del nucleo in NSE prodotto dalla combustione in shell del silicio
approssima 1:1M (Ye assume ora un valore prossimo a 0:42) si determina una prima
fase di forte contrazione. Questo fatto implica un aumento del momento di Fermi degli
elettroni con la conseguenza di far crescere ulteriormente il tasso di cattura elettronica
sui protoni dei nuclei di NSE e sui pochi protoni liberi (Yp = 10 4 ). Si viene a creare,
14
Capitolo 1. Supernovae
Fig. 1.3: Andamento dell'indice adiabatico in funzione della densita per valori ssati dell'entropia
specica per barione come indicati in unita di k (cortesia di Wolfgang Hillebrandt).
B
pertanto, una situazione in cui le catture elettroniche si autoamplicano. Il risultato e
catastroco perche viene sottratta improvvisamente la principale sorgente della pressione
che si opponeva alla gravita che prende quindi il sopravvento. Gli eventi che ne conseguono
costituiscono un insieme complesso ed unico nello studio della sica delle strutture stellari.
1.6.1 Il collasso del nucleo
Parte delle nozioni che verranno ora descritte sono ricavabili da appropriate considerazioni
siche sulle proprieta e sullo stato del sistema in analisi, tuttavia, il piu deriva dall'analisi
di risultati di calcoli numerici espliciti di idrodinamica mono e pluridimensionale.
Si puo mostrare come sia possibile vericare in modo complementare l'instaurarsi
dell'istabilita che porta al collasso, con il vantaggio di poter anche stabilire che il collasso
non potra aver termine se non quando la materia avra raggiunto densita nucleari ( 2 1014 gr cm 3 ).
Si consideri l'indice adiabatico della materia del nucleo in NSE
@lnP
=(
)
(1.5)
@ln Ye ;S
E noto ([4]) che quando l'indice adiabatico di un sistema termodinamico sorretto dalla
gravita scende sotto 4/3 tale sistema diviene dinamicamente instabile nel senso che, per
esempio, ad una variazione negativa delle dimensioni segue un ulteriore diminuzione delle
stesse. Nella materia in NSE del nucleo in pre-collasso l'entropia specica per barione e
ormai prossima a 1kB (si ricorda che in una stella di sequenza principale S 40kB
1.6. SUPERNOVAE A COLLASSO GRAVITAZIONALE
15
Fig. 1.4: Descrizione schematica della situazione sica di un nucleo in NSE di una stella massiccia nella
fase iniziale del collasso. Il bruciamento in shell del silicio ha prodotto un core in NSE che ha raggiunto
la massa di Chandrasekhar divenendo instabile. Le specie nucleari piu abbondanti nel core in NSE sono
rappresaentate da ferro e nichel. I neutrini liberati a seguito delle catture elettroniche sono ancora liberi
di sciamare. (Cortesia di Ewald Muller).
per nucleone, kB costante di Boltzmann). Come si puo derivare da un'analisi della Fig.
1.3 (adattata da [4]) per un tale valore dell'entropia e per i valori di densita assunti
dal nucleo in NSE citati nel paragrafo precedente, assume valori gia molto prossimi a
4/3. La quantita cruciale da considerare e comunque l'indice adiabatico eettivo, che, in
accordo con [4] approssimeremo con
4 1 ÆY
= + ( )( e )
3 Ye Æln
(1.6)
Quando il secondo termine a destra dell'uguaglianza assume valori negativi (ovvero quando
la cattura elettronica diventa dominante) scendera decisamente sotto 4/3 rendendo il
nucleo instabile e libero di collassare. Un'analisi ulteriore della Fig. 1.3 mostra anche che
ritorna a valori nettamente superiori a 4/3 solo quando supera 2 1014 gr cm 3 .
Solo in questo caso la struttura puo nuovamente stabilizzarsi su un equilibrio idrostatico
per l'eetto della pressione dei neutroni degeneri che si oppone alla gravita. Si deve notare che quanto detto vale rigidamente se durante il collasso la materia mantiene, come in
eetti succede, valori di S bassi. Non e solo la cattura elettronica a rendere instabile per
collasso in nucleo di \Fe" di una stella massiccia. Infatti, processi di fotodisintegrazione
del tipo
56
F e + ! 134 He + 4n 124 Mev
impediscono che, a seguito della contrazione, l'energia interna cresca e contribuiscono a
loro volta a ridurre sotto 4=3. A partire da un'equazione di stato per materia degenere
16
Capitolo 1. Supernovae
a temperatura nita si puo ottenere per l'indice adiabatico:
=
4
3
f (; Ye) (
2
3
2
@lnT
)
@ln S
(1.7)
dove f e una funzione positiva nota dei due parametri. Qualora, all'aumentare di , la
temperatura -come caso estremo- non cresca, scende sensibilmente sotto 4=3.
Prima di discutere in qualche dettaglio l'evoluzione del collasso e opportuno accennare
preliminarmente ad alcune nozioni:
1) Gran parte del collasso si svolge adiabaticamente. L'unica fonte di perdita di energia e data dai neutrini di deleptonizzazione (emessi a seguito delle catture elettroniche)
limitatamente alla prima fase del collasso. (Come si vedra, quando la densita supera
3 1010 gr cm 3 i neutrini non riusciranno piu a sfuggire (\neutrino trapping") e il numero leptonico totale tendera a conservarsi per diversi secondi, un tempo lungo rispetto
al tempo di collasso.
2) La variazione globale di entropia specica e bassa. Sommando la variazione di entropia
durante il collasso, prima e durante il neutrino trapping, si stima che S 0:5. Pertanto la bassa entropia iniziale rimane bassa. Di conseguenza i nuclei resteranno legati
(l'entropia di A nucleoni e circa A volte maggiore dell'entropia di un nucleo di numero
atomico A) e la pressione continuera ad essere dominata dagli elettroni relativistici (e
dai neutrini dopo il neutrino trapping). Pertanto il collasso non potra arrestarsi se non a
densita nucleari.
3) La cattura elettronica avviene prima sui protoni dei nuclei. Successivamente, quando
questi cominciano a presentare shell neutroniche chiuse, diviene importante la cattura
elettronica sui (pochi) protoni liberi (Yp 10 4 ).
4) Il tempo scala di caduta libera (free fall time) del core e stimabile in ff = (G) 1=2 10 2 s. Dal calcolo idrodinamico si ottiene un tempo di collasso c = 10 1 s.
Durante il collasso tutto il core in NSE assume un campo di velocita negative. Si puo
stimare analiticamente ([7], [6]), e si verica in dettaglio con simulazioni numeriche, che
mentre il collasso procede il campo di velocita assume delle propieta che impongono di
suddividere il core in due parti dinamicamente distinte ed usualmente denite inner core
(IC) e outher core (OC).
l'IC assume velocita che, a tempo ssato, risultano di modulo crescente al crescere
della distanza dal centro, v (r) / r. Pertanto, durante tutto il collasso, l'IC evolvera
attraverso strutture tra di loro omologhe. Un prolo di velocita del tipo v (r) / r non
puo comunque estendersi a Mr comunque grandi. Infatti, ad un determinato valore di
massa (il cui valore dipende dal tempo) la velocita raggiunge un valore massimo (in
17
1.6. SUPERNOVAE A COLLASSO GRAVITAZIONALE
Fig. 1.5: Descrizione schematica della situazione sica del nucleo di una stella massiccia in fase piena
di collasso al tempo del neutrino trapping quando la densita centrale ha raggiunto 1012 g cm 3 .
Il campo di velocita ha diviso il nucelo in due parti. La massima velocita di collasso si registra a circa
0:8M. Nella parte interna del core (IC) i neutrini sono denitivamente intrappolati e la massa di
Chandrasekhar non potra piu variare (si veda il testo). Nel core esterno i neutrini riescono ancora a
sciamare senza eccessiva diÆcolta. (Cortesia di Ewald Muller).
c
p
modulo), per poi assumere un prolo con andamento decrescente del tipo v / 1= r. Si
conviene di separare l'IC dall'OC nel punto dove il modulo della velocita raggiunge un
massimo. L'evoluzione dinamica dell'OC assume un andamento tipico di free fall. (Al
crescere della coordinata lagrangiana nell'OC la velocita decresce poiche le densita sono
sempre piu basse). Si puo dimostrare che la massa dell'IC omologo corrisponde al valore
istantaneo assunto dalla massa di Chandrasekhar ove si consideri il numero leptonico
totale al posto di quello solo elettronico MIC MCh = 5:83(YL)2 M dove YL = Ye + Y
mentre Y = (ne n e )=nbarioni . Pertanto la massa dell'IC tendera a diminuire n tanto
che i neutrini prodotti dalla cattura elettronica saranno liberi di sfuggire immediatamente
dal core. Queste proprieta sono chiaramente illustrate dalla gura 1.6.
Nell'IC, o, piu precisamente, in una parte rilevante di questo, le velocita di collasso si
mantengono al di sotto della velocita locale del suono mentre l'opposto si verica in tutto
l'OC. Il punto che gode della proprieta di avere velocita uguale, in modulo, alla velocita
locale del suono viene denito punto sonico. Per quanto accennato precedentemente,
durante il collasso le coordinate lagrangiane del punto di separazione tra IC e OC e quelle
del punto sonico non rimangono rigidamente ssate se non dopo che il numero leptonico
totale non vari piu (neutrino trapping).
La zona piu centrale dell'IC e la prima a raggiungere densita confrontabili con quelle
nucleari ed e pertanto la prima dove il collasso tende ad arrestarsi. Questo succede poiche a
densita elevate prevale la componente repulsiva delle forze forti. Gli strati dell'IC progres-
18
Capitolo 1. Supernovae
rv
max
(t2)
rv
max
(t1)
0
M(r)
r
t1
V
homologous infall
V~r
t2>t1
sonic point
supersonic infall
Mic (t2)
Mic (t1)
Fig. 1.6: Proli di velocita assunti dal core in collasso in due tempi successivi t1 e t2 con t2 > t1 . Le
curve tratteggiate rappresentano i proli della velocita locale del suono ai tempi t1 e t2 ed incrociano i
proli di velocita della materia nei rispettivi punti sonici. Si noti come il campo di velocita separi il
core in due zone distinte: quella interna, omologa, con velocita localmente subsoniche e quella esterna,
supersonica, in caduta libera. (Cortesia di Ewald Muller).
V
shockwave
M(r)
0
r
shocked
matter !
bounce
"la
st
go
od
supersonically
falling outer core
m
ho
olo
gy
"
+
Fig. 1.7: Proli di velocita assunti dal core in collasso in tre tempi successivi: 1) l'ultimo modello realmente omologo subito prima che il collasso inizi ad arrestarsi al centro, 2) il collasso si e appena arrestato
nella zona piu centrale ma non si e ancora prodotta l'onda d'urto di decompressione, 3) si e generata
l'onda d'urto ed ha gia attraversato una piccola zona del core esterno invertendone temporaneamente il
campo di velocita. (Cortesia di Ewald Muller).
1.6. SUPERNOVAE A COLLASSO GRAVITAZIONALE
19
sivamente piu esterni vanno successivamente ad arrestarsi su questa riducento improvvisamente la loro velocita. Mentre questo succede i nuclei dell'IC perdono progressivamente le
loro superci individuali mergendo in una sorta di mega-nucleo. Come si vedra nel paragrafo successivo la completa neutronizzazzione deve attendere ancora qualche secondo.
Va comunque ricordato che la distribuzione asintotica della materia nucleare conterra
ancora un certo numero di elettroni e di protoni (in ragione di n : p : e = 8 : 1 : 1).
L'inner core rappresenta pertanto la prima meta, circa, in massa, della nascente stella di
neutroni. Subito dopo che tutto l'IC ha raggiunto e superato (di un fattore almeno 3)
la densita nucleare, in prossimita del suo bordo esterno si sviluppa un'onda d'urto la cui
formazione e favorita dal riassestamento dell'IC su densita nucleari di equilibrio (come si
vedra meglio nel successivo paragrafo 7). L'onda d'urto inizia a propagarsi verso l'esterno
attraverso l'OC che sta ancora collassando, muovendosi quindi in una materia dotata di
campo di velocita opposte. Ma questo aspetto, di per se, non costituisce un problema
di maggiore rilevanza. L'energia iniziale dell'onda d'urto coincide con l'energia cinetica
posseduta dall'ultima struttura dell'IC realmente omologa (subito prima che la zona piu
centrale tenda ad arrestarsi e che il prolo di velocita v (r) / r non sia piu applicabile
a tutto l'IC). Si stima, e si ottiene da simulazioni idrodinamiche del collasso, un'energia
iniziale dell'onda d'urto dell'ordine di 105152 erg .
A questo punto fa la sua apparizione un aspetto fondamentale del problema, aspetto
che gia da diversi anni preclude una comprensione certa dei meccanismi sici che presiedono al collasso e all'esplosione delle supernovae di tipo II. Appare infatti evidente
che qualora si riuscisse a trasferire alle parti esterne al nucleo in NSE tutta l'energia
posseduta dall'onda d'urto si otterrebbe un'esplosione in grado di rispecchiare molti dei
requisiti osservativi. Tuttavia, il fatto che l'onda d'urto inizi a propagarsi da un punto
localizzato alla base dell'OC, e che prima di trasferirsi alle zone piu esterne debba attraversarlo, implica una perdita di energia dell'onda d'urto la cui entita puo essere tale
da inibire totalmente l'espulsione degli strati esterni o da determinare un evento di supernova di energia drammaticamente piu bassa di quella osservata. Le perdite di energia sono
dovute prevalentemente a fenomeni di fotodisintegrazione dei nuclei dell'OC in nucleoni
liberi o in nuclei e, in un secondo tempo, anche a perdite per emissione neutrinica.
Infatti, all'attraversmanto dell'onda d'urto, l'OC subisce un netto aumento di densita e
temperatura da cui ne risulta profondamente modicato lo stato sico. In pratica e come
se si stesse riassestando l'equilibrio statisitico nucleare dell'OC su congurazioni piu energetiche. Se le perdite sono troppo elevate l'onda d'urto non riesce a propagarsi attraverso
il nucleo esterno e va in stallo (stalled shock). L'onda d'urto si denisce in stallo quando la
sua posizione geometrica rispetto al centro non varia piu mentre, nel contempo, la massa
del core esterno le uisce attraverso dissipandone l'energia. Il destino di un'onda d'urto
in questa situazione e quello di estinguersi rapidamente.
20
Capitolo 1. Supernovae
Tuttavia, il fenomeno di supernova, cioe l'espulsione ad alte velocita ad alta temperatura dell'inviluppo stellare, viene osservato in stelle di massa anche elevata. Appare,
quindi, chiaro che esistono delle imprecisioni nella sica che si sta usando oppure che eetti
sici determinanti non sono stati presi in considerazione. Nella formazione di una stella
di neutroni si liberano circa 1053 erg mentre le energie osservate in un tipico evento di
SN II (energia irraggiata piu energia cinetica) sono dell'ordine di 1051 erg . La dierenza
(che costituisce il 99 per cento dell'enegia totale dell'evento) viene emessa sotto forma
di neutrini. Solo una parte estremamente piccola dell'energia trasportata dai neutrini
sarebbe suÆciente, ove utilizzabile, ad espellere l'inviluppo.
1.6.2 L'evento neutrinico
Il collasso del nucleo di una stella di massa iniziale maggiore di 12M e in grado di
liberare, a spese dell'energia gravitazionle, un'energia dell'ordine di:
1
M
R
1
) 3 1053 ( )( 2 ) 1 erg
(1.8)
R2 R1
M 10Km
dove R1 ed M sono la massa ed il raggio iniziale del nucleo in NSE ed R2 il raggio nale.
La seconda eguaglianza segue da una stima di R1 ed R2 eettuabile assumendo che il
nucleo transisca da una situazione di degenerazione relativistica degli elettroni ad una
analoga per i neutroni. Per gli elettroni, seguendo la statisitica di Fermi, si puo scrivere
E = GM 2 (
R1 =
analogamente per i neutroni
(bne )1=3 h
pF
108cm
(1.9)
(nn )1=3 h
10Km
(1.10)
mn c
Dove b = 9=32 2 , ne ed nn rispettivamente il numero degli elettroni e dei nucleoni, mn la
massa del nucleone, h e c la costante di Plank e la velocita della luce, e pF il momento di
Fermi degli elettroni ( 10Mev ).
R2 =
Un aspetto importante da chiarire e che l'energia potenziale gravitazionale viene in
massima parte convertita in energia degli elettroni prima e poi, a seguito della cattura elettronica sui protoni, in quella dei neutrini. Solo una frazione trascurabile viene trasferita
in energia cinetica. La situazione sica del tutto inusuale che si viene a creare durante il
collasso e che da un certo istante in poi i neutrini non sono piu in grado di abbandonare
liberamente l'IC (neutrino trapping). Questo fenomeno comincia gia a manifestarsi per
densita 3 1010 gr=cm 3 quando il libero cammino medio dei neutrini diviene confrontabile con le dimensioni dell'inner core in collasso. Per valori inferiori della densita
1.6. SUPERNOVAE A COLLASSO GRAVITAZIONALE
21
i neutrini di cattura elettronica su protoni legati o liberi erano riusciti a sciamare senza
diÆcolta. Dopo il neutrino trapping il numero leptonico YL = Ye + Y inizia a conservarsi
e dovranno passare diversi secondi perche tutti i neutrini vengano emessi e si completi il
fenomeno di deleptonizzazione dell'IC (che costituisce la prima meta circa della nascente
stella di neutroni).
La principale interazione che i neutrini subiscono nella materia densa e dovuta a
scattering coerente sui nuclei. Il libero cammino medio e esprimibile dalla relazione:
A
)( ) 1 (E ) 2 cm
(1.11)
N 2 12
dove 12 e la densita espressa in 1012 gr cm 3 , E l'energia dei neutrini espressa in Mev, A
ed N sono rispettivamente il numero di massa ed il numero dei neutroni del nucleo tipico;
nel coeÆciente numerico si e tenuto conto del fatto che l'interazione e dominata dalle
correnti neutre. Durante il collasso A ed N variano sia a causa della neutronizzazione dei
nuclei per cattura elettronica sia per i processi di agglutinamento dei nuclei al crescere
della densita (che niranno per conuire, al raggiungimento delle densita nucleari, in un
mare di neutroni degeneri). Si stima che, quando 1014 g cm 3 , A sia dell'ordine di
1000.
109 (
Al crescere della densita si viene a creare una condizione ancora piu estrema. Quando
3 6 1011 gr cm 3 il tempo scala di diusione dei neutrini diventa molto piu
lungo del tempo scala del collasso. I neutrini sono degeneri e riempiono il loro proprio
mare di Fermi in cui i possibili livelli liberi si trovano solo ad alte energie. Pertanto, i
nuovi neutrini emessi nelle catture elettroniche devono possedere energie elevate e avranno
liberi cammini medi ancora piu ridotti. Cos come per i fotoni in una stella \normale",
qui i neutrini sono gli unici costituenti ad essere soggetti alle equazioni del trasporto e
posseggono una loro propria supercie di ultimo scattering (neutrinosfera) che in analogia
con la fotosfera viene denita dalla relazione
Z 1 dr
2
(r) = r 1:
(1.12)
3
A dierenza di quanto succede con la fotosfera, le cui dimensioni non dipendono fortemente dalla lunghezza d'onda dei fotoni, in questo caso le dimensioni della neutrinosfera
variano apprezzabilmente al variare dell'energia associata con i neutrini. L'IC in collasso,
una struttura stellare, seppure instabile, in cui la sorgente di pressione e dovuta agli
elettroni ed ai neutrini degeneri, e divenuto, in pratica, una \stella di neutrini" la cui
(neutrinosfera) e ora visibile con telescopi neutrinici. Quando la densita raggiunge valori
vicini a 1012 gr cm 3 si stabilisce una condizione denita di -equlibrio: le reazioni
deboli, in particolare la reazione e + p ! n + e , vanno in equilibrio con le proprie
inverse. Tuttavia, il -equlibrio costituisce una situazione di equilibrio dinamico nel senso
22
Capitolo 1. Supernovae
che la frazione di elettroni continua in eetti a diminuire, seppure piu lentamente, perche
il valore di Ye dipende dalla densita e dalla temperatura. Dopo il raggiungimento del
-equlibrio l'entropia rimane praticamente costante ed il collasso procede in forma nettamente adiabatica. A densita ancora piu alte la lunghezza d'onda associata ai neutrini
diviene confrontabile con le dimensioni dei nucleoni, o minore di queste. L'interazione di
scattering tra questi due componenti riduce il cammino libero medio a qualche centimetro.
L'energia dei neutrini supera i 150 Mev .
In questa situazione sica il processo di denitiva deleptonizzazione (neutronizzazione
della materia), che in pratica viene a coincidere con quello di rareddamento della prima
meta circa della proto-stella di neutroni (MIC 0:8M ), avviene su un tempo-scala
dell'ordine dei 10 secondi:
3R2
(1.13)
(c)
dove R e il raggio dell'IC collassato, il libero cammino medio dei neutrini, c la loro
velocita (si assume la velocita della luce). Questa relazione e derivata dalla random walk
theory nella quale si trova che il numero di urti che una particella con libero cammino
medio sfuggira da una sfera di raggio R dopo un numero di interazioni N = 3R2 =2 .
Dopo che l'IC ha completato il collasso ed e ritornato su condizioni di equilibrio
idrostatico (mantenendo un'entropia specica S 1B ), ma non ha ancora concluso
il processo di deleptonizzazione e sta ancora intrappolando gran parte dei neutrini nora
prodotti , l'OC inizia ad accrescersi sulla prima meta della proto-stella di neutroni gia
formata. Si usa anche denire l'OC come lo \shocked core" (S 10B ), infatti esso costituisce quella frazione di proto-stella di neutroni che prima di collassare denitivamente
e stata attraversata dall'onda d'urto (che comunque non ne ha invertito il campo di velocita). Soltanto dopo che sono trascorsi circa 0:4 secondi da quando l'IC si e riaggiustato
su una congurazione nale di equilibrio idrostatico, l'OC termina la fase di accrescimento e la proto-stella di neutroni ha raggiunto la sua massa nale. Tuttavia, mentre
nella parte interna (l'ex IC o \un-shocked core") i neutrini sono ancora intrappolati, i
neutrini derivanti dalla neutronizzazione dell'OC sono stati emessi con relativa facilita a
causa della minore densita locale ed hanno determinato quello che viene denito \burst di
neutronizzazione immediato", che ha luogo in pochi decimi di secondo (a partire da circa
0.3 sec dopo la ne del collasso dell'IC), ed ha un picco di luminosita neutrinica di circa
5 1053 erg sec 1 ed e costituito soltanto da neutrini elettronici.
Tra i costituenti dell'IC i neutrini sono quelli che interagiscono piu debolmente (perche
non interagiscono ne attraverso forze elettomagnetiche ne attraverso quelle forti) e sono,
pertanto, quelli che si possono muovere piu liberamente guidando l'evoluzione della protostella di neutroni. Quando i primi neutrini dell'\un-shocked core" iniziano a diondere
23
1.7. L'enigma dell'esplosione
verso l'esterno l'equilibrio dei processi viene simultaneamente ripristinato in un processo dinamico in cui i nuovi neutrini che provengono dalla cattura elettronica sui protoni
colmano i livelli di energia lasciati vuoti dai neutrini che hanno iniziato a sciamare. (La
proto-stella di neutroni viene attraversata da una corrente neutrinica che, prima che intervenga il rareddamento denitivo, indurra in essa degli eetti termici non trascurabili).
I neutrini, nel loro cammino verso la neutrinosfera, degradano progressivamente di energia attraverso varie forme di interazioni la cui natura dipende dallo stato della materia
attraversata e dall'energia istantanea dei neutrini. Particolarmente eÆcienti risultano le
interazioni di scattering con gli elettroni e le creazioni di neutrini da coppie di elettroni
e viceversa. Quando i neutrini abbandonano denitivamente il core collassato attraverso
la neutrinosfera possiedono un'energia media di 10 Mev e presentano uno spettro termalizzato. Pertanto, per ogni neutrino che emerge dalla parte piu interna del core, circa 10,
in media, lasceranno la neutrinosfera. Uno dei 10 deve essere un e che trasporta anche
il numero leptonico. Se il resto dell'energia e egualmente distribuito tra le altre specie
neutriniche (e ; e ; ; ; ; ), ci saranno, in media, 1.5 neutrini per ogni specie.
In pratica, il 99% dell'energia potenziale gravitazionale e stata convertita in
energia degli elettroni e dei neutrini e successivamente dispersa da quest'ultimi
determinando nella proto-stella di neutroni solo eetti termici secondari. Solo
una frazine dell'ordine dell'uno per cento dell'energia potenziale e stata convertita in energia cinetica della materia e la si ritrova nell'energia posseduta
dall'onda d'urto.
La luminosita dei neutrini e esprimibile attraverso la relazione:
L 1037 R2 T 4 erg sec
1
(1.14)
dove il coeÆciente numerico contienetiene un certo numero di costanti, R e il raggio in
centimetri della neutrinosfera e T la sua temperatura espressa in Mev. Se si considera
che tutto il processo di emissione neutrinica e durato circa 10 secondi, che l'energia totale
(L t) e di circa 1053 erg , si ritrova il valore dell'energia media dei neutrini cui si e
precedentemente accennato.
1.7 L'enigma dell'esplosione
Mentre nell'inner core gia collassato si stanno gia vericando gli eventi neutrinici che
sono stati descritti, l'onda d'urto generata in prossimita del suo bordo esterno, si sposta
attraverso la materia ancora in collasso dell'OC. A causa dell'inerzia, al momento della
massima contrazione l'IC supera la densita nucleare di un fattore che si stima essere
compreso tra le 3 ed anche le 10 volte (l'esatta valutazione dipende dalla conoscenza, ancora incerta, dell'equazione di stato della materia nucleare) per tornare, successivamente,
24
Capitolo 1. Supernovae
ad una congurazione di equilibrio con il tempo-scala tipico di una oscillazione radiale
( 10 3 s). La decompressione violenta (re-bounce) produce delle onde soniche che, a
partire dal centro, si propagano sfericamente verso l'esterno no a conuire in un'onda
d'urto la cui energia iniziale, in accordo con [8], e stimabile in
ESW;0 4 10 1051 erg
(1.15)
un'energia confrontabile con l'energia cinetica dell'ultima congurazione omologa dell'IC
e nominalmente suÆciente a determinare l'espulsione dell'inviluppo ed a caratterizzare
adeguatamente tutto il fenomeno di supernova.
Si stima anche ([4] e relative citazioni) che nell'attraversamento di una massa M
dell'OC l'onda d'urto vada soggetta a perdite di energia che, qualora M sia espresso in
masse solari, risultano essere:
E = 1:6 1:8 1052 M erg
(1.16)
determinate dalla fotodisintegrazione dei nuclei in nucleoni liberi o nuclei e dall'emissione
neutrinica (dopo che l'onda d'urto e emersa dalla neutrinosfera). E facile convincersi che
nella maggior parte dei casi (in pratica gia per M > 12 15M ) la massa dell'OC e
tale da smorzare totalmente l'onda d'urto o, al piu, da rendere trascurabile, ai ni della
produzione di una supernova, l'energia di un'onda d'urto che riuscisse eventualmente
ad attraversarla. E facile anche intuire come sarebbe suÆciente utilizzare una frazione
trascurabile dell'energia emessa dai neutrini per impedire il damping dell'onda d'urto.
E invalso l'uso di denire prompt explosion l'evento in cui l'onda d'urto riesce ad attraversare indenne l'OC senza che sia necessario l'intervento di altre sorgenti di energia
(promt 10msec). Con il termine delayed explosion si denisce invece l'evento in cui, su
tempi lunghi (delayed 1sec), una parte dell'energia dei neutrini e utilizzata per riattivare un'onda d'urto andata precedentemente in stallo o in procinto di andarci. Tuttavia
l'interazione tra i neutrini emessi dall'IC collassato e la materia attraverata dall'onda
d'urto e molto evanescente.
I risultati delle simulazioni numeriche sono in parte ancora contraddittori: si sono
ottenute prompt explosions solo in casi di massa del nucleo in NSE particolarmente ridotte
e non sempre tali risultati sono stati riprodotti da altri gruppi di ricerca. In un caso ([9]),
anche questo non riprodotto da altri gruppi, si e ottenuta una delayed explosion. Pertanto
il motivo sico che rende possibile una supernova a collasso del nucleo continua a sfuggire
ad una chiara comprensione. Il lettore interessato puo trovare una ampia analisi dei
risultati ottenuti nora in [?].
Tra le ipotesi operative che riscuotono maggiore attenzione trova posto l'idea che nella
zona intermedia tra l'onda d'urto che sta per andare in stallo (a circa 108 cm dal centro)
e la neutrinosfera (a circa 106 cm dal centro) si formi una hot bubble (S > 100) generata
1.7. L'enigma dell'esplosione
25
Fig. 1.8: Descrizione schematica della situazione sica di un core collassato di una stella massiccia
al tempo in cui l'onda d'urto sta provando ad attraversare il l'outher core (OC). La zona piu interna
del core ( 0:4M) si e ormai stabilizzata su densita nucleari ( 2 1014 g cm 3) ma sta ancora
trattenendo leptoni (e pertanto ancora denibile un valore della massa di Chandrasekhar). In una zona
subito a ridosso di questa (di un'estensione di circa 0:4M) la materia si presenta ancora sotto l'aspetto
strutturato di nuclei molto pesanti; anche qui i neutrini sono ancora parzialmente intrappolati. Lo shock,
che ha iniziato a propagarsi dal bordo esterno dell' inner core, sta ora attraversando l'ex outher core
ancora in collasso dissipando la propria energia nella fotodisintegrazione dei nuclei di NSE e, solo in
parte limitata, nell'invertire temporaneamente il campo di velocita della materia in collasso.
Fig. 1.9: Andamento temporale della posizione radiale di punti massa selezionati di un core in collasso nel
caso di una failed prompt explosion. Come si puo osservare, a tempi lunghi non sopravvive alcun campo
di velocita positive e la materia continuera ad accrescersi indenitamente sull nucleo stellare collassato.
In questo modello non e stato preso in considerazione alcun contributo dei neutrini nel sopperire alle
dissipazioni energetiche cui va soggetta l'onda d'urto. (Cortesia di Wolfgang Hillebrandt).
26
Capitolo 1. Supernovae
Fig. 1.10: Esempio di successfull prompt explosion. Anche in questo caso si e assunto che i neutrini non
contribuiscano alla riattivazione dell'onda d'urto tuttavia le dimensioni ridotte dell' outher core hanno
evitato che l'energia dell'onda d'urto venisse completamente assorbita per cui, a tempi lunghi, sopravvive
un campo di velocita positive che inne coinvolgera tutto l'inviluppo stellare. (Cortesia di Wolfgang
Hillebrandt).
dalle interazioni neutriniche, che sospinga, in virtu di una forte epansione, l'onda d'urto
verso le zone esterne. Le interazioni che determinano la formazione della "bolla calda"
sono principalmente dovute a scattering neutrinico su elettroni ed annichilazione di coppie
neutriniche ( ! e e+ ). L'eÆcienza di queste reazioni dipende dalla luminosita dei neutrini, dal loro spettro e, anche, dalla loro obliquita (coseno dell'angolo di propagazione).
Tutti parametri la cui determinazione precisa dipende, in ultima analisi, da un trattamento corretto del trasporto neutrinico all'interno, ma non solo, della neutrinosfera. (Le
tre zone rilevanti per il trasporto neutrinico sono: la zona interna \spessa" (approssimativamente coincidente con l'ex IC), la zona intermedia \semitrasparente" prossima alla
neutrinosfera (l'ex OC) e la zona \sottile" di fuga, a raggi maggiori). La trattazione esplicita del trasporto neutrinico costituisce un problema teorico di notevole diÆcolta che
puo essere arontato in vari modi, sempre, comunque, con delle assunzioni semplicatrici che no ad oggi rendono ancora incerta l'aÆdabilita della soluzione ottenuta. Si
deve anche accennare al fatto che e stato suggerito che l'istaurarsi di instabilita convettive a ridosso dell'onda d'urto possano facilitare l'assorbimento neutrinico ed aiutare la
formazione della bolla calda.
Sebbene sia attualmente ritenuta poco percorribile, non e stata completamente abbandonata l'ipotesi che il meccanismo di promt explosion possa avere successo qualora
possa subire modica la trattazione di alcuni parametri sici, per esempio nella direzione
che varino le proprita del core in NSE prima o durante il collasso. Ne caso specico, se
la separazione tra IC ed OC potesse essere posta in regioni piu esterne l'energia iniziale
1.8. L'espulsione dell'inviluppo
27
Fig. 1.11: Descrizione schematica della situazione sica che si avrebbe nel caso in cui una parte
dell'energia trasportata dai neutrini potesse eettivamente essere utilizzata nel creare una bolla calda
al ridosso del fronte d'urto. I neutrini che diondono dalla neutrinosfera della protostella di neutroni (le
cui propieta siche sono riportate in gura) interagiscono in vario modo con la materia a raggi maggiori
di circa 100 Km cedendo localmente energia. (Cortesia di Ewald Muller).
dell'onda d'urto sarebbe maggiore e le sue perdite, nell'attraversamento di un OC meno
massivo, sarebbero minori.
1.8 L'espulsione dell'inviluppo
Se l'onda d'urto riesce a superare indenne l'outher core non trovera ulteriori ostacoli
no al raggiungimento della supercie. Infatti, il mantello di una stella di massa medio
alta in fase evolutiva nale, e gravitazionalmente poco legato e la materia che lo compone e formata da nuclei di basso numero atomico (valori di S ancora alti). Inoltre, a
causa dei bassi valori di , quando l'onda d'urto lo attraversa, il mantello esterno al core
e ancora dinamicamente fermo. Per superare gli ostacoli teorici descritti nei paragra
precedenti, che precludono ancora la conoscenza dell'energia propria dell'onda d'urto al
momento in cui essa abbandona il core in collasso e di come tale energia dipenda dalle
proprieta del progenitore stellare, e invalso l'uso di disaccoppiare i problemi da studiare
separando l'analisi del collasso da quella dell'espulsione dell'inviluppo. Assumendo un
valore dell'energia da associare ad un'onda d'urto generata articialmente a partire dalla
base dell'inviluppo stellare, si analizzano gli eetti indotti dal suo passaggio al variare dei
parametri d'interesse.
Il tempo di attraversamento dell'inviluppo da parte dell'onda d'urto varia da qualche
ora a qualche giorno e dipende principalmente dal raggio della struttura. Anche il rapporto
28
Capitolo 1. Supernovae
tra energia meccanica e termica depositate nell'inviluppo dall'onda d'urto dipendono dalla
densita dello stesso. In genere, il fenomeno viene ben descritto da tre parametri principali:
energia dell'onda d'urto uscente dal core, raggio iniziale e massa della struttura stellare.
Tuttavia, anche la composizione chimica dell'inviluppo e la sua distribuzione rivestono un
ruolo non secondario e non solo nella determinazione dell'aspetto spettroscopico e della
sua evoluzione. Nei casi piu comuni (progenitori super giganti rosse) l'energia cinetica
totale depositata dell'inviluppo ammonta a 1051 erg mentre quella irraggiata dal campo
elettromagnetico durante tutto l'evoluzione della SN risulta essere dell'ordine di 1049 erg .
Esistono diverse simulazioni numeriche dell'evoluzione di una SN di assegnate proprieta
che consentono di determinare le curve di luce attese in varie bande pressate e l'evoluzione
temporale degli spettri.
Quando l'onda d'urto arriva in supercie il primo e piu immediato eetto e quello di
innalzarne la temperatura della fotosfera stellare di diverse migliaia di gradi determinando
l'emissione un usso ultravioletto molto intenso ma di breve durata (\UV ash", minuti).
Immediatamente dopo iniziano gli eetti dell'espansione. La curva di luce che si viene a
creare e una combinazione di diversi eetti sici che, in ultima analisi, concorrono alla
determinazione delle dimensioni della supercie di ultimo scattering dei fotoni (Rfotosfera )
e della sua temperatura ( Te ). Infatti, in prima approssimazione, si puo pensare che
2
la curva di luce sia rozzamente determinata da L(t) / Rfotosfera
Te4 . Le dimensioni della
fotofera dapprima cresceranno, seguendo l'espansione dell'inviluppo. Successivamente,
con il diminuire della densita delle zone piu esterne (le piu veloci), la fotosfera regredira
in massa (ma, almeno inizialmente, non in raggio). La temperatura e determinata da
un complesso contributo di fenomeni tra cui il rareddamento dovuto all'espansione ed il
riscaldamento determinato dalla ricombinazione e dai decadimenti radiattivi. La presenza
di materiale radiattivo (Ni ! Co ! F e) e vericata sperimentalmente e sta ad indicare
che una parte del nucleo in NSE viene espulsa insieme all'inviluppo. Evidenze sperimentali sembrerebbero mostrare che la massa di Ni espulso varia al variare della massa
iniziale della stella (0:07 < MNi =M < 0:12) e che questo viene parzialmente rimescolato
nell'inviluppo presumibilmente a causa di instabilita che si vengono a creare al passaggio
dell'onda d'urto. I proli di velocita osservati mostrano che osservando strati sempre piu
interni la velocita diminusce. Un fenomeno ampiamente spiegabile in termini di prolo
iniziale di densita dell'inviluppo stellare e di proprieta dell'onda d'urto che accellera passando dalle zone interne ad alta densita a quelle esterne di densita piu bassa. Quando la
densita dell'inviluppo in espansione si riduce apprezzabilmente i fotoni duri prodotti dai
decadimenti radiattivi non sono piu riassorbiti e diventano osservabili con strumentazione
X e da satellite o da pallone.
Il confronto tra i risultati dei modelli teorici parametrizzati come precedentemente descritto e i dati osservativi dovra contribuire a denire questioni aperte relative all'eettiva
1.9. La nucleosintesi delle SNe II
29
energia posseduta dall'onda d'urto, a problemi di mescolamento della materia attraversata da questa, alla quantita e qualita del materiale radiattivo presente nell'inviluppo e
sottratta al collasso, e quanto di altro che ancora costituisce problema aperto.
1.9 La nucleosintesi delle SNe II
Un aspetto importante delle Supernovae e quello di produrre materia di alto numero
atomico e di immetterla ad alta velocita nel mezzo interstellare. Le Supernovae \fanno"
quello che il Big-Bang non e riuscito a fare. In realta, nelle SN II la nucleosintesi che
avviene duranto l'evento esplosivo e abbastanza trascurabile. Riveste, invece, importanza
rilevante l'aspetto che nell'espulsione dell'inviluppo vengono ceduti al mezzo interstellare
tutti i prodotti della nucleosintesi quiescente avvenuta lungo tutto l'arco della vita della
stella. Si tratta pertanto di materia ricca di nuclei multipli di (nuclei compresi). In
tutto il contesto del riciclaggio di materia da parte delle SNe II, aspetto meno rilevante
assume, invece, seppur presente, la produzione di elementi prossimi al Ferro. A titolo di
semplice esempio, si puo considerare che in una stella di 25M di tipica popolazione II
all'atto della formazione sono presenti circa 18:7M di Idrogeno, 6:2M di Elio e meno di
un decimo di massa solare di elementi di numero atomico maggiore (e tra quest'ultimi C,
N ed O ne costituivano piu del 50 percento). Determinando teoricamente tutta la storia
evolutiva della stella e dei rispettivi bruciamenti nucleari ed atti di rimescolamento interno
si trova che questa al momento di esplodere come Supernova rimette in circolazione circa
12M di H, 10M di He, 0:2M di C, 0:05M di N, 1M di O, 0:25M
di Ne, 0:05M di Mg, 0:04M di Si, e, forse, 0:07M di \Fe". Per determinare
questi valori si e anche assunto che circa 1:4M di materia in NSE rimangano bloccate in
una stella di neutroni e che eventuali eventi di vento stellare abbiano interessato solo zone
esterne non toccate dai bruciamenti nucleari. E interessante notare come i rapporti degli
elementi pesanti rimessi in circolo da questo modello teorico siano molto simili ai rapporti
degli stessi elementi cos come si trovano in natura. Normalizzando ad uno di essi, per
esempio il Carbonio, si ottiene che N/C fornito dal modello teorico e 0:2 mentre in
natura N/C osservato e 0:25. Similmente O/C stimato teoricamente dal modello e
circa 4, contro un valore osservato di circa 3. Per i rimanenti elementi rilevanti si ha,
rispettivamente, Ne/C 1 contro 0:5; Na/C 0:05 contro 0:05; Mg/C contro 0:2;
Al/C 0:08 contro 0:1; Si/C 0:18 contro 0:2. (Si tratta peraltro degli elementi
piu abbondanti escludendo l'Idrogeno e l'Elio la cui produzione deve essere fatta risalire
al Big-Bang). Unica eccezione puo essere costituita dal Ferro. Mentre la produzione
di elementi di numero atomico maggiore del Fe deve essere fatta risalire ai processi di
cattura neutronica lenta nelle stelle di massa intermedia, appare evidente che il grosso
della nucleosintesi di elementi multipli ed una produzione ridotta di Fe debba essere
attribuita alle SNe II. Si vedra nel prossimo capitolo come, sebbene tra diÆcolta teoriche
30
Capitolo 1. Supernovae
ancora piu rilevanti di quelle esposte qui per le SNe a collasso del nucleo, appaia possibile
attribuire alle SNe Ia il grosso della produzione di Fe nella nostra e nelle altre galassie.
Appendici
1.A La massa limite di Landau-Chandrasekhar
L'esistenza di una massa limite per materia sorretta da elettroni degeneri relativistici e derivabile in forma
semplice, sebbene approssimata, linearizzando l'equazione dell'equilibrio stellare
P = P P P GM
(1.17)
M
M
M 4R4
dove P e P rappresentano rispettivamente la pressione centrale e quella superciale, che, per semplicita,
assumiamo nulla. Inoltre, confondendo M con M , ed assumendo che la pressione sia solo dovuta agli
elettroni degeneri relativistici
4 3
1
P = (32 )1 3 h c
Y4 3
(1.18)
4
m
se ne deriva che il gadiente di pressione non sara piu bilanciato quando, a meno di un fattore dell'ordine
dell'unita,
h c 3 2
M > 1 2
m 2Y 2
(1.19)
G
dove m la massa del nucleone, h la costante di Plank diviso 2 e G la costante di gravita. Se le varie
costanti sono date in unita CGS, M sara espressa in grammi. Un altro approccio molto istruttivo allo
stesso problema si ottiene considerando l'Hamiltoniana del nucleo stellare. Se si assume che il contributo
all'energia gravitazionale sia dovuto solo ai nucleoni e quello all'energia cinetica solo agli elettroni si puo
scrivere
2
X
(1.20)
H =T +U
= p q_ G(n m )
c
c
ext
ext
=
=
e
=
e
n
=
=
n
e
n
n
grav
i
R
i
i
n
dove p e il momento degli elettroni relativistici, n il numero1 3di nucleoni ed R il raggio della struttura.
Attribuendo agli elettroni il momento di Fermi p = (bn ) h=R dove la costante b assume il valore
b = 9=322, h e la costante di Plank ed n il numero di elettroni con momento no a p , l'espressione
precedente si puo riscrivere come:
b1 3 n4 3 hc G(n m )2
H=
(1.21)
i
n
F
e
=
e
F
=
=
e
n
R
R
n
Un valore negativo del membro destro di questa relazione comporta la presenza di una instabilita in
quanto pregura un campo di velocita negative, infatti q_ = . Pertanto quando
@H
@p
31
32
Capitolo 1. Supernovae
M > b1
2
=
3 2
ch
=
G
m 2Y 2
n
e
la pressione dovuta agli elettroni non sara piu in grado di bilanciare la gravita.
(1.22)
Bibliograa
[1] Cappellaro, E., Turatto, M., Tsvetkov, D., Bartunov, O.S., Pollas, C. Evans, R., and
Hamuy, M., 1997, A&A, 322,431
[2] Cox & July
[3] Dogget and Branch:1985, A.J., 90,2303
[4] Muller, E.
[5] Polcaro, V.F.
[6] Yahil
[7] Goldrake
[8] Monchmayer
[9]
33
Capitolo 2
Sistemi Binari e Supernovae Termonucleari
L' esistenza di eventi a carattere esplosivo con energie dell'ordine di 1051 erg in sistemi
stellari antichi (t > 10 Gyr) si scontra con l'impossibilita di giusticarne l'origine in
stelle singole di piccola massa, le uniche ad essere ancora in fase di bruciamento attivo
in eta avanzate. Sappiamo infatti, che tali stelle sono fatalmente destinate a terminare
la loro esistenza rareddandosi sotto la forma di Nane Bianche. E peraltro da notare
che tali strutture degeneri di Carbonio ed Ossigeno risultano dei potenziali detonatori
non appena si ipotizzi l'eÆcienza di qualche meccanismo in grado di elevarne la massa
no alla massa critica di Chandraseckar. Una tale evidenza ha orientato la ricerca dei
progenitori di tali eventi nella direzione dei sistemi stellari binari. E infatti possibile
che fra le componenti di un sistema binario esistano forme di interazione con scambio
di massa che possono determinare la formazione di eventi di alto contenuto energetico
su tempi-scala particolarmente lunghi. Come si vedra in questo capitolo, esiste infatti
la possibilita che il tempo-scala evolutivo globale di un sistema binario possa risultare
nettamente piu lungo di quello della componente meno massiccia. In aggiunta, esiste in
natura un numero molto elevato di sistemi binari che costituiscono almeno la meta degli
oggetti stellari del disco della nostra galassia. Il numero di parametri sici che caratterizza
il comportamento evolutivo di un sistema binario e cos elevato che una opportuna scelta
di questi consente di realizzare cammini evolutivi che conducono a stati nali esplosivi.
Sara peraltro necessario vericare se il numero di sistemi binari che ci si aspetta si formino
proprio con quei parametri risulti compatibile con quanto mostrato dalle osservazioni in
termini di frequenza statistica degli eventi esplosivi. Nel seguito deniremo quindi il
quadro evolutivo che si viene a creare in caso di binarieta investigando come i parametri
sici del sistema inuenzino i cammini evolutivi delle stelle che lo costituiscono.
34
2.1. Proprieta di un Sistema Binario
35
2.1 Proprieta di un Sistema Binario
Le componenti stellari di un sistema binario, soggette alla reciproca attrazione gravitazionale, percorrono orbite i cui parametri sono ricavabili, di norma, dalle comuni leggi
della meccanica classica. Nel seguito si fara riferimento ad orbite circolari, assumendo,
come e ragionevole, che la circolarizzazione sia intervenuta in tempi brevi rispetto a quelli
evolutivi delle componenti. Se la separazione A del sistema e elevata (A 10(56) R ), e
molto probabile che, a causa dell' interazione con il campo gravitazionale generale della
galassia, il legame si sciolga prima che avvenga qualsiasi rilevante fenomeno evolutivo in
ciascuna delle due componenti. Qualora il legame non venisse sciolto l'evoluzione delle
componenti si svolgerebbe come nel caso di stelle singole indipendenti in quanto la distanza tra le due componenti e molto piu grande dei raggi raggiungibili dalle stesse nel corso
della loro evoluzione. Invece, se la separazione non e elevata (Amin 10 A=R 104 )
occorrera considerare l'esistenza di fenomeni di scambio di massa tra le due componenti
che, intervenendo in istanti precisi dell'evoluzione di ciascuna di esse, modicheranno, talvolta in maniera radicale, il quadro evolutivo descritto precedentemente per stelle singole.
Si noti che lo scambio di massa inuira anche sui parametri orbitali del sistema binario.
Negli approfondimenti viene data una descrizione sintetica delle proprieta siche assunte dello spazio in prossimita di un sistema binario. In gura 2.1 e riportato l'andamento
dell' energia potenziale lungo l' asse che congiunge le due componenti stellari di massa
M1 ed M2 di un sistema con rapporto di massa q = M2 =M1 = 0:5. Assumendo la separazione A come unita di lunghezza, la somma delle masse delle componenti come l'unita
di massa e ! 1 come quella di tempo, la primaria occupa la buca di potenziale che ha
sede nell'origine mentre la secondaria occupa quella posta ad una distanza unitaria. Il
massimo relativo centrale di g. 2.1 corrisponde al punto lagrangiano interno L1 (cfr.
A1). E intuitivo comprendere come, qualora una delle due componenti espanda no colmare completamente la propria buca di potenziale (riempimento totale del proprio lobo
di Roche, cfr. A1), la materia superciale possa uire sull' altra componente. Sempre con
riferimento alla g. 2.1, si noti che i due massimi esterni del potenziale corrispondono ai
punti lagrangiani L2 ed L3 (cfr. A1). E di nuovo immediato comprendere come, qualora
questi punti venissero raggiunti dalla materia stellare, questa sara ora in grado di abbandonare facilmente il sistema. La presenza della forza centrifuga determina la formazione
di buche di potenziale \aperte".
In denitiva, se una delle componenti stellari del sistema espande il proprio raggio no
a L1 la materia superciale potra uire attraverso questo dalla stella stessa alla compagna.
Se ambedue le componenti sono espanse la materia uira dal sistema allo spazio esterno
attraverso L2 o L3 .
Le fasi evolutive in cui si verica un'accentuata espansione degli strati esterni e quindi
36
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.1: Andamento dell'energia potenziale lungo l'asse x congiungente le due componenti stellari di un
sistema binario con q = 0:5. I massimi coincidono con i punti lagrangiani interno ed esterni (! A1).
un possibile contatto con il primo punto singolare L1 , sono, di norma, l'uscita dalla
Sequenza Principale e le successive fasi di Gigante Rossa (primo ramo delle giganti, ramo
asintotico ed eventuali altre fasi successive di escursione al rosso). Ricordiamo inoltre
che, mentre in fase di uscita dalla Sequenza Principale l'espansione avviene su tempiscala lunghi, nelle fasi evolutive lungo la traccia di Hayashi, i tempi-scala di crescita del
raggio divengono molto piu rapidi.
E invalso l'uso di denire contatto di tipo A quello che si realizza quando L1 (ovvero la
prima supercie critica, o anche lobo di Roche, cfr. A) viene raggiunto in fase di evoluzione
in uscita dalla Sequenza Principale con abbondanza centrale di H ancora maggiore di zero.
Vengono invece deniti contatti di tipo B e C quelli che si hanno rispettivamente in fasi
evolutive di gigante rossa o di ramo asintotico. Evidentemente, nel primo caso si e in
presenza di un sistema binario abbastanza stretto mentre negli altri due casi la separazione sara, in generale, piu elevata. In tale contesto conviene analizzare separatamente
le proprieta strutturali e gli aspetti evolutivi di strutture stellari in fase di cessione o di
acquisizione di massa.
2.2 Strutture stellari indotte a cedere massa
Nello studio dell'andamento evolutivo a lungo termine di stelle indotte a cedere massa
poiche le loro superci hanno raggiunto L1 (ovvero, per essere entrate in contatto con il
2.2. Strutture stellari indotte a cedere massa
37
proprio lobo di Roche) ed in forza dell'esistenza di un potenziale quale quello riportato in
g. 2.1, e utile acquisire alcune nozioni preliminari.
Un primo aspetto riguarda il comportamento strutturale della stella soggetta a perdita
di massa. Conviene infatti valutare se in seguito ad una variazione di massa M la
struttura reagisca diminuendo ovvero aumentando il proprio raggio.
Nel primo caso si potra pervenire ad un trasferimento di massa stazionario (M_ costante) e stabile per lungo tempo. Perche questo succeda e necessario che gli eetti
evolutivi, che inducono un generale aumento del raggio, si manifestino su tempi scala
piu lunghi di quelli del riaggiustamento strutturale su raggi minori, indotto della diminuzione di massa. Ambedue le condizioni sono ben vericate quando a cedere massa sono
strutture vicine alla loro Sequenza Principale. Ad una fuoriuscita dal lobo di Roche segue
un trasferimento di massa ed un riaggiustamento su raggi minori; ambedue i fenomeni
si interrompono momentaneamente non appena le dimensioni della stella rientrano nuovamente all'interno del lobo di Roche. Il processo riprende quando l'evoluzione impone
nuovamente il superamento del lobo di Roche da parte degli strati superciali. E evidente
che, in natura, il trasferimento di massa assume un aspetto continuo e stazionario.
Nel secondo caso, invece, quando ad una diminuizione di massa segue un aumento del
raggio il processo risulta reazionato positivamente ed il tasso di trasferimento di massa
subira un aumento indiscriminato. Esiste tuttavia un limite alla crescita di M_ determinato
dall' inerzia posseduta dalle strutture stellari nel riaggiustarsi su raggi maggiori. In altri
termini, il trasferimento di massa risulterebbe di eÆcienza costantemente crescente solo
se il riaggiustamento su raggi maggiori che lo segue avvenisse istantanemante e non,
come invece di fatto deve avvenire, con tempi termodinamici. Situazioni in cui ad una
diminuizione di massa segue un aumento del raggio sono tipiche di strutture in fase di
gigante rossa o di AGB a causa delle proprieta siche degli inviluppi convettivi e, in
particolare, della gia discussa dipendenza della traccia di Hayashi dalla massa della stella.
Un ulteriore aspetto da tenere in considerazione riguarda le variazioni del lobo di
Roche al variare del rapporto di massa q in seguito allo scambio di massa oppure a causa
della variazioni di altri parametri del sistema (per esempio della sua energia). Si tratta,
quindi, di un problema complesso la cui migliore soluzione e quella data dallo studio
numerico del fenomeno con cui determinare gli andamenti temporali delle variabili siche
e, in particolare, i valori assunti da M_ . Trascurando la variazione delle dimensioni del
lobo di Roche, si possono tuttavia fare delle utili stime preliminari.
Nel caso in cui il contatto sia di tipo A, ovvero qualora la componente entri in contatto con il proprio lobo di Roche durante l'evoluzione in uscita dalla Sequenza Principale,
i tempi di riassestamento strutturale risultano sempre piu piccoli dei tempi caratterisitici
del trasferimento di massa. Per queste strutture si puo assumere come tempo di riasses-
38
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
tamento il tempo-scala di Kelvin cos come dato dal rapporto tra l'energia gravitazionale
e la luminosita della struttura
GM 2
k /
RL
oppure, esprimendo le quantita in unita solari e k espresso in anni:
(2.1)
M2
(2.2)
RL
E facile vericare che, per un vasto spettro dei valori di massa, k si mantiene sempre,
per piu di un'ordine di grandezza, al di sotto del valore tipico del tempo-scala di trasferimento di massa tm , dove tm M=M_ 3R=R_ a sua volta una frazione del tempo-scala
evolutivo e , con e 1010 M=L ([4]) espresso in anni per M ed L in unita solari. Poiche
in questa fase evolutiva ad una diminuizione di massa segue una diminuizione di raggio,
si verichera una condizione di trasferimento stazionario in cui per M_ M=t si ottiene 10( 7 9) M yr 1 avendo utilizzato per M tutto il valore della massa e per t
il tempo evolutivo in uscita dalla Sequenza Principale (Xc < 0:6). I valori ricavati da
modelli numerici realistici non si discostano troppo da queste stime approssimative.
k 2 107
Durante la fase di trasferimento stazionario la stella riempie con continuita il proprio
lobo di Roche facendo uire fuori da questo solo la materia che l'evoluzione avrebbe portato
ai maggiori raggi che non sono di fatto raggiunti, limite che viene spesso rispettato anche
a fronte dell'evoluzione temporale delle dimensioni del lobo di Roche. Il trasferimento
di massa cessa di essere stazionario quando viene a mancare la condizione primaria che
lo ha determinato, cioe la risposta strutturale di diminuire il raggio ad una diminuizione
di massa, oppure nel caso in cui le dimensioni del lobo di Roche varino su tempi scala
inferiori a quelli di riaggiustamento strutturale. In genere, la condizione di stazionarieta
del trasferimento viene persa prima del raggiungimento della fase di sub-giant branch.
Condizioni totalmente diverse si vericano invece nei casi di contatto di tipo B o C.
In questi casi le proprieta siche dei profondi inviluppi convettivi sono tali da indurre
un aumento di raggio ad una diminuizione di massa. Questa proprieta, vericabile con
precisione attraverso lo studio numerico, e in parte ricavabile da considerazioni elementari
cos come riportato nell'approfondimento B.
Appare subito chiaro che nel caso in cui l'aumento del raggio e positivamente reazionato dalla perdita di massa attraverso il punto lagrangiano interno, l'unico freno ad un
processo di trasferimento di massa a valanga e costituito dall'inerzia posseduta dalla
struttura a riaggiustarsi su raggi maggiori. Facendo uso del tempo-scala termico su cui
l'inviluppo si riaggiusta e ricordando che ora all'interno della struttura e presente un
nucleo compatto si ha:
2.3. Stelle soggette ad accrescimento di massa
39
Mcore Menv
(2.3)
LR
dove il tempo e espresso in anni e le variabili a destra sono in unita solari. Facendo
riferimento a casi reali e possibile rendersi conto che le varie coppie realistiche di Menv e
env forniscono un valore del tasso di perdita di massa che, entro un' ordine di grandezza,
risulta pari a:
env = 3:5 107
M
(2.4)
M_ termico env 10 2 M yr 1
env
In conclusione, il processo di trasferimento di massa a causa del riempimento del proprio lobo di Roche da parte di stelle in ramo di gigante o in ramo asintotico, avviene su
tempi scala termici e con valori spesso prossimi a 10 2 M yr 1. Di norma il processo di
trasferimento, una volta avviato, si ferma solo quando la massa dell'inviluppo si riduce a
pochi decimi di massa solare. In pratica, tutto l'inviluppo viene ceduto. Alla ne del processo, della primaria non rimane che il nucleo degenere circondato da un piccolo inviluppo
radiativo, alla cui base si trova una shell di bruciamento in via di estinzione. E anche
possibile, sebbene meno probabile, che il trasferimento abbia termine perche la struttura
recede dalle condizioni espanse per motivi evolutivi (innesco di un nuovo bruciamento
centrale).
2.3 Stelle soggette ad accrescimento di massa
Non sempre la materia ceduta dalla stella che riempie il proprio lobo di Roche puo venire
accettata dalla compagna.
La materia trasferita deposita sulla superce della stella in accrescimento un'energia:
GM M_
(2.5)
R
Esiste peraltro un limite sico alla luminosita che una struttura stellare puo emettere
senza che gli strati esterni divengano gravitazionalmente slegati. Tale luminosita limite
(limite di Eddington) e data dalla relazione:
Lgrav =
4cGM
(2.6)
e
dove le costanti c e G hanno il signicato usuale di velocita della luce e di costante
gravitazionale e e e l'opacita superciale per la quale si puo assumere con buona approssimazione lo scattering Thomson (e = 0:3 cm2 gr 1).
Confrontando le due espressioni si ottiene una relazione per il tasso di accrescimento
limite che chiameremo M_ limite di Eddington:
Ledd =
40
oppure, in unita solari:
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
4cR
M_ edd =
e
(2.7)
R
M_ edd = 10 4
M yr 1
(2.8)
e Per una stella di tipo solare si avra M_ edd 3 10 4 M yr 1 e per una 9M M_ edd 10 3 M yr 1. Se M_ di accrescimento supera M_ edd la materia trasferita non viene accettata. In questo caso l' energia depositata eccede quella irraggiabile e la materia accresciuta si riscalda e si dispone su una congurazione espansa simile a quella di una
gigante rossa.
Confrontando i tassi di trasferimento ricavati nel paragrafo precedente con il valore
assunto da M_ edd per stelle non evolute di Sequenza Principale (condizione tipica della
secondaria al momento del primo episodio di riempimento di lobo di Roche da parte della
primaria) se ne deriva che la materia trasferita sara totalmente accresciuta soltanto se la
primaria realizza un contatto di tipo A. In questo caso si parlera di evoluzione del sistema
di tipo conservativo poiche durante lo scambio di massa vengono conservati energia e
momento angolare del sistema.
Negli altri casi, generalmente non conservativi, la materia trasferita sulla secondaria
espandera no a riempire prima il lobo di Roche di questa e, successivamente, anche i
volumi contenuti dalle superci equipotenziali esterne di forma ellissoidale (contatti con
L2 o L3 ). Questa congurazione viene denita di \Common Envelope" (CE) in quanto
le due componenti si trovano ad orbitare all' interno di un unico inviluppo comune. L'
espansione dell' inviluppo comune non si arresta no a che non viene raggiunta la prima
superce critica con singolarita nel punto L2 . Data la forma assunta dal potenziale (g.
2.1), la materia sara ora in grado di abbandonare liberamente il sistema. Tale processo
potra arrestarsi solo quando avra termine la causa che lo ha determinato, quindi non
prima che la primaria abbia ceduto tutto il suo inviluppo oppure che essa receda dalla sua
congurazione di gigante rossa per motivi evolutivi. Confrontando i tempi scala evolutivi
della fase che ci riguarda con quelli tipici del trasferimento di massa, si potra concludere
che la seconda evenienza deve avere bassa probabilita di vericarsi.
2.4 Evoluzione in Fase di Inviluppo Comune
Alcuni aspetti evolutivi di un sistema binario immerso in un inviluppo comune non sono
ancora noti con precisione. Sicuramente il fatto che le componenti stellari si muovano
2.4. Evoluzione in Fase di Inviluppo Comune
41
all'interno di un mezzo di densita che, sebbene bassa, non e trascurabile, determinera
l'insorgere di attriti di varia natura. Questi avranno l'eetto di far perdere energia al sistema stellare e di riscaldare ed espandere ulteriormente l'inviluppo comune. Ragionevolmente ci si puo attendere che le orbite, da circolari, possano assumere un andamento
spiraleggiante verso il centro del sistema e che la materia che compone l'inviluppo venga
spinta verso i punti lagrangiani esterni e fatta uire liberamente fuori dal sistema. L'
entita di tale fenomeno e di diÆcile quanticazione se non attraverso una trattazione
idrodinamica completa ancora lontana dall' essere realizzata.
Esistono tuttavia degli aspetti dell'evoluzione in fase di CE che sono conoscibili e quanticabili con un buon livello di approssimazione. Riassumendo quanto e ragionevolmente
noto e stimabile negli eetti, si puo aermare che:
si sa perche si determina un CE
dati i parametri del sistema (masse e separazione) si conosce se e quando ha luogo
un trasferimento di massa che porta ad un CE
si conoscono le cause che determinano la conclusione di un episodio di CE
si stima con ragionevolezza la massa nale della secondaria
Inoltre, se si assume, come e ragionevole fare, che il tempo-scala su cui procede la perdita
di massa dal sistema sia piccolo rispetto ai tempi scala evolutivi delle componenti, e anche
possibile conoscere la quantita di massa persa dal sistema e la massa e la composizione
chimica del resto della primaria. Questo restringe il numero delle incognite del problema
ad una sola, sebbene di cruciale importanza: se e quanto cambia la separazione del sistema
a causa di un evento di CE.
Per stimare la nuova separazione A0 assunta dopo il CE da un sistema di separazione
iniziale A, Iben e Tutukov ([6]) suggeriscono la relazione:
M1;r M2
A
(2.9)
M12
essendo rispettivamente M1 ; M1;r ed M2 la massa originale della primaria, quella del
suo resto alla ne del CE e la massa della secondaria che si assume invariata a seguito all'episodio di CE. Il parametro e un parametro libero adimensionale dell'ordine
dell'unita (cfr. C).
A0 = Con gli strumenti teorici di cui ci si e dotati e possibile elaborare il quadro evolutivo
di un sistema binario al variare dei suoi parametri iniziali (principalmente separazione e
massa delle componenti).
42
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
2.5 Sistemi Prodotti dall'Evoluzione in Common Envelope
Il primo trasferimento di massa inizia quando la primaria entra in contatto con il proprio
lobo di Roche. L' istante evolutivo in cui cio accade dipende dalla massa della primaria
mentre l'aspetto assunto dal trasferimento di massa (stazionario o critico) dipende principalmente dalla separazione iniziale A. Facendo riferimento a stelle di massa piccola o
intermedia, si ottiene, ssata la massa, che per piccole separazioni si verica un trasferimento per lunga durata conservativo (della massa totale e degli altri parametri sici del
sistema) durante il quale la massa ceduta dalla primaria viene totalmente accresciuta
dalla secondaria. Il trasferimento conservativo avra comunque termine quando, a seguito
dell'evoluzione, la primaria perdera le sue proprieta strutturali vicine a quelle di una stella
di sequenza principale.
Per separazioni medie o medio-alte (A 102 103 R ) la fase di primo trasferimento
inizia quando la primaria ha raggiunto la fase di RGB o di AGB. In ambedue i casi si
verichera una fase di common envelope al termine della quale della primaria originaria
non rimane che il solo nucleo circondato dalla shell di bruciamento attiva in quel momento.
La composizione chimica e lo stato temodinamico del nucleo dipendono dalla massa iniziale
della primaria e dalla fase evolutiva in cui si e vericato il trasferimento di massa. La
secondaria non ha variato in modo apprezzabile la propria massa e la separazione A0 del
sistema puo essere variata secondo i dettami della relazione 2.21. Se il trasferimento ha
interessato stelle di RGB il nucleo residuo della ex-primaria e composto essenzialmente
di He e sara degenere nella sua componente elettronica se la massa iniziale della stella
e minore di 2:3M , ovvero si trattera di una stella di He in bruciamento centrale 3
per masse superiori. Se il trasferimento ha avuto inizio in fase di AGB Il resto della exprimaria e costituito essenzialmente di C-O ed e degenere per masse iniziali no ad 8M ,
valore superiore di massa cui limiteremo i nostri riferimenti sia per motivi di semplicita
sia perche stelle inferiori a 8M sono di gran lunga piu numerose in quanto favorite dall'
andamento della funzione di massa.
Si deve notare che se il contatto con il proprio lobo di Roche da parte della primaria
non e avvenuto lungo tutto il RGB questo non potra avvenire se non lungo l' AGB a
nucleo degenere di C-O gia sviluppato. Infatti, dopo l'innesco centrale dell'elio, il raggio
totale diminuisce e, durante tutta la fase successiva di HB, non cresce mai al di sopra
dei valori raggiunti alla cima dell' RGB se non dopo l'esaurimento dell' elio al centro e a
nucleo degenere di C-O ben sviluppato.
Il sistema intermedio che emerge dal primo Common Envelope e quindi un sistema piu
legato di quello originario, con la primaria ridotta ad una nana in fase di rareddamento
e con il rapporto di massa invertito. E invalso l'uso, per evitare l'insorgere di confusioni,
di continuare ad attribuire il nome di primaria alla componente originariamente piu massiccia anche se nel sistema intermedio questa proprieta e divenuta di pertinenza della
2.5. Sistemi Prodotti dall'Evoluzione in Common Envelope
43
secondaria.
Le modalita evolutive del sistema intermedio non si discosteranno, in linea di principio,
da quelle del sistema originario. Quando la secondaria entrera in contatto con il proprio
lobo di Roche si potra vericare un trasferimento di tipo conservativo se il valore A0 della
separazione e suÆcientemente basso da determinare l' inizio del trasferimento di massa
durante la fase di uscita dalla Sequenza Principale. Viceversa, per valori di A0 non piccoli,
si potra vericare un secondo episodio di common envelope. Il fatto che durante il secondo
episodio di fuoriuscita dal lobo di Roche la materia viene generalmente trasferita su una
nana bianca, non modica infatti il quadro schematizzato precedentemente per il caso di
una secondaria di Sequenza Principale. Ricordando che:
R
(2.10)
M_ edd = 10 4 M yr 1
ke
si puo stimare come per una nana bianca le condizioni per accettare in modo quiescente
la massa accresciuta siano ancora piu restrittive di quelle richieste per stelle di Sequenza
Principale. In aggiunta, come si vedra nel paragrafo dedicato agli accrescimenti di materia
su nane bianche, esiste una ulteriore condizione sica che induce l'espansione su larghi
raggi della materia accresciuta gia per tassi di molto inferiori a quello limite di Eddington.
Qualora il secondo episodio di trasferimento di massa dia luogo ad un secondo episodio
di Common Envelope, il risultato sara un sistema nale composto da una nana bianca di
massa invariata (il resto della primaria) e dal nucleo della compagna che ha determinato
l'insorgere del secondo episodio di trasferimento di massa.
La composizione e lo stato termodimamico di quest' ultimo dipendono dalla massa
originale della secondaria e dal valore assunto da A0 . Si trattera di una una stella (oppure
di una nana) di elio se la secondaria e originariamente piu (oppure meno) massiccia di 2.3
M ed il contatto e stato di tipo B, cioe lungo il ramo delle giganti. Se invece il contatto e
stato di tipo C, lungo il ramo asintotico, il resto della secondaria sara comunque una nana
di C-O. La nuova separazione A00 del sistema potra essere variata secondo i dettami della
relazione 2.21, nel senso che A00 A0 essendo gia A0 A. In particolare puo succedere
che la separazione A00 risulti particolarmente ridotta ( R ) determinando in tal caso
l'insorgere di fenomeni relativistici.
Appare chiaro quanto elevata sia la molteplicita di sistemi nali che possono formarsi
a partire da sistemi iniziali con parametri dierenti. I casi piu frequenti che possono
vericarsi in sistemi che evolvono attraverso due fasi di Common Envelope sono riportati
nella tabella 1 di questo capitolo insieme ad indicazioni sulla massa iniziale delle componenti ed alla fase evolutiva in cui ciascuna di esse ha realizzato la fuoriuscita dal proprio
lobo di Roche. A titolo di sussidio visivo, la presenza nel sistema nale di una nana di
44
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
He e stata indicata con il simbolo Æ, quella di una stella di elio in bruciamento centrale
3 con il simbolo e, inne, quella di una nana di C-O con il simbolo . Il simbolo
# sta ad indicare che quel sistema puo evolvere in quello sottostante. Infatti, nei casi
in cui il risultato di un episodio di Common Envelope sia la produzione di una stella di
He, questa evolvera in tempi rapidi in una nana di C-O quindi il sistema che abbiamo
precedentemente denito come nale sara in eetti un sistema transitorio (altri episodi
di CE sono possibili in questo caso). E anche possibile, come sara mostrato nel seguito,
che prima che la stella di He evolva possa gia intervenire una interazione di scambio con
la compagna modicando ulteriormente il quadro evolutivo.
Altri casi meno frequenti sono costituiti da sistemi nali composti da (nana di O-Ne +
nana di C-O), (nana di O-Ne + stella di He), (nana di O-Ne + nana di He) qualora si
estendano le considerazioni precedenti no a stelle di massa iniziale pari a 12M .
2.6 L' Evoluzione dei Sistemi Finali
Ci si aspetta che i sistemi nali che emergono da due o piu episodi di common envelope
presentino delle separazioni molto ridotte (dell'ordine di qualche raggio solare). Se questo
e il caso il sistema diviene un eÆciente irraggiatore di onde gravitazionali. La variazione
temporale della separazione A del sistema, in accordo con [7], e esprimibile come segue
dA
1 64G3 M1 M2 (M1 + M2 )
=
(2.11)
dt
A3
5c5
dove si intende con A la separazione attuale del sistema (A00 ), e con M1 ed M2 le masse
attuali delle componenti (M1;r ed M2;r ), G la costante di gravita e c la velocita della luce.
Integrando questa equazione e possibile ottenere il tempo caratteristico merg in cui le due
componenti coalescono:
5c5
A4
256G3 M1 M2 (M1 + M2 )
oppure, ponendo le varie grandezze in unita solari ed esprimendo merg in anni:
merg =
(2.12)
A4
(2.13)
merg = 1:5 10
M1 M2 (M1 + M2 )
Si noti come per masse nali dell'ordine della massa solare e separazione nale minore di
3R le componenti del sistema giungeranno in coalescenza in un tempo minore di quello
di vita dell' universo (tempo di Hubble). Per separazioni nali dell'ordine del raggio solare
o meno, separazioni che in base alle considerazioni del paragrafo precedente sono del tutto
ammissibili, il tempo di coalescenza sara addirittura di qualche decina di milioni di anni.
8
45
2.6. L' Evoluzione dei Sistemi Finali
TIPOLOGIE DEI SISTEMI FINALI
sistema nale
range m. pr. & fase range m. sec. & fase
0:7 2:3M (RGB) 0:7 2:3M (RGB)
Æ
Æ
nana di He + nana di He
Æ
nana di C-O + nana di He 0:7 8:0M (AGB) 0:7 2:3M (RGB)
#
due stelle di He
2:3 8:0M (RGB) 2:3 8:0M (RGB)
#
nana di C-O + stella di He 2:3 8:0M (AGB) 2:3 8:0M (RGB)
due nane di C-O
0:7 8:0M (AGB) 0:7 8:0M (AGB)
Tab. 2.1: Tabella esemplicativa della tipologia dei sistemi nali che emergono da due episodi di common
envelope. Sono indicati gli intervalli di massa iniziale della primaria (range m. pr.) e della secondaria
(range m. sec.) e, tra parentesi tonde, la fase evolutiva di rispettiva interazione con il proprio lobo di
Roche.
46
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Durante un evento di coalescenza si verica ancora una volta un trasferimento di massa
per riempimento di un lobo di Roche. Contrariamente a quanto avviene normalmente,
questa volta il riempimento del lobo di Roche non e determinato da variazioni evolutive
del raggio della componente stellare che insiste in questo. In realta sono le dimensioni
stesse del lobo di Roche che diminuiscono a causa della diminuizione della separazione del
sistema. Gli eventi di coalescenza piu frequenti coinvolgono due nane bianche. Sono anche
possibili eventi di coalescenza che coinvolgono una stella di He (con bruciamenti nucleari
ancora attivi) e una nana di C-O. I due casi dieriscono in modo sostanziale. Infatti, nel
caso di due nane, il loro andamento strutturale tipico, in cui ad una diminuizione di massa
segue un aumento di raggio, ci induce a richiamare le nozioni che in casi normali ci hanno
fatto concludere in favore della formazione di un sistema a inviluppo comune. Tuttavia,
nel caso presente, l' evoluzione terminale dei parametri del sistema e molto piu rapida
dei tempi di riassestamento strutturale (k =system 103 ). Per questa ragione si e portati
a ritenere che la nana che riempie per prima il proprio lobo di Roche vada incontro ad
un evento di dissoluzione totale nendo col formare un disco massivo e spesso, orbitante
intorno alla compagna. Dal disco la materia viene successivamente accresciuta sulla nana
rimasta integra ad un tasso il cui valore non e di facile determinazione.
Nel caso in cui sia una stella di He (con bruciamento centrale 3 attivo) a riempire il
proprio lobo di Roche a causa della variazione delle dimensioni di questo per emissione
di onde gravitazionali da parte del sistema, si puo invece pervenire ad un trasferimento
quasi stazionario. Questo in virtu del fatto che una stella di He ha un comportamento
strutturale simile a quello di una analoga struttura in Sequenza Principale di H ed anche
perche il contatto viene raggiunto a separazioni del sistema molto piu alte che nel caso
precedente. Quest' ultimo fatto implica un'evoluzione molto piu lenta dei parametri del
sistema (merg / A4 ).
Riassumendo, le possibili strade che l'evoluzione nale di un sistema binario soggetto
a due episodi di CE puo seguire sono:
una nana di He che accresce He da una nana ad un tasso di non immediata determinazione
una nana di C-O che accresce He ad un tasso denibile con precisione da opportuni
calcoli evolutivi (accrescimento da stella di He) oppure ad un tasso non immediatamente determinabile (accrescimento da nana di He)
una nana di C-O che accresce C+O da una nana ad un tasso di non immediata
determinazione.
Sebbene poco probabili, si possono vericare talune altre situazioni, come, nello specico,
quelle che vedono coinvolte come accettori di massa nane di O-Ne (discendenti da stelle di
2.7. Gli Accrescimenti Finali
47
massa originaria compresa tra 8 e 12M ). In questo volume, per motivi di semplicita,
non ci si occupera in modo esplicito di tali sistemi, nonostante il fatto che essi possano
essumere rilevanza nell'interpretazione di specici fatti osservativi. Ad ogni buon conto,
l'applicazione dei principi generali espressi per sistemi con componenti di massa minore di
8M consente di ricavare facilmente il quadro evolutivo di sistemi binari interagenti dotati
di componenti con massa iniziale al di fuori del range studiato qui in modo esplicito.
2.7 Gli Accrescimenti Finali
L'evoluzione nale dai sistemi stellari appena descritti, consiste di una prima fase in
cui il trasferimento di massa induce sulla stella che accresce materia degli eetti termici
locali o diusi. In una seconda fase, qualora il materiale accresciuto raggiunga condizioni
siche che determino l'insorgere di combustioni nucleari, si possono vericare bruciamenti
a carattere quiescente oppure di tipo esplosivo.
Va preliminarmente notatato che alle fenomenologie descritte nel paragrafo precedente,
relative a fasi nali di sistemi che abbiano subito almeno due fasi evolutive di CE, va in
ogni caso aÆancata quella relativa a sistemi che entrano in fase di contatto nale dopo un
solo episodio di common envelope. Per questi sistemi, in cui, di norma, una nana di C-O
accresce H in forma conservativa da una compagna in uscita dalla Sequenza Principale, il
tasso di accrescimento M_ H e denibile con suÆciente precisione attraverso una opportuna
trattazione numerica del problema.
Nei quattro paragra che seguono verra indagata la risposta termica di una bianca
di C-O che accresce materia con diversa composizione chimica evidenziando le situazioni
che portano ad un innesco termonucleare. Negli ultimi due paragra di questo capitolo
saranno invece studiati due casi in cui l'innesco termonucleare e a carattere esplosivo
Il quadro nale cui siamo pervenuti nei paragra precedenti consiste di tipologie ben
denite: nane che accrescono H soltanto da strutture stellari non degeneri, nane che
accrescono He da strutture sia degeneri sia non degeneri e, inne, nane che accrescono
C+O solo da strutture degeneri.
In questa scala di eventi, piu e nuclearmente evoluta la materia accresciuta, piu alto e il
grado di esoticita del sistema ma piu basse sono le diÆcolta nella trattazione del problema.
Infatti, almeno per il momento, un sistema doppio degenere stretto (per esempio due nane
di C-O che possano mergere) rimane ancora un' astrazione teorica. Non sembra a priori
vietato che un tale sistema si formi, tuttavia, perche questo succeda, si deve assumere
che esistano dei processi sici che ne discriminino con precisione il cammino evolutivo e
non ci sono prove sperimentali che confermino che questo succeda eettivamente. D' altro
canto l'accrescimento di C+O su una nana di C-O costituisce un problema semplice da
studiare in quanto non ci si aspettano processi di combustione nucleare multipla nelle zone
superciali della stella che riceve massa. All'estremo opposto, nel caso di accrescimento
48
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
di H, ci si puo ragionevolmente attendere, in particolari condizioni, l'esistenza di due
fasi di combustione durante le quali l'idrogeno venga prima converito in elio e questo,
successivamente, in C-O. Un aspetto che complica la trattazione del problema. Un sistema
binario in cui una nana accresce idrogeno e, invece, un sistema di bassa esoticita ed e
suÆcientemente dimostrato che esiste in natura una vasta molteplicita di sistemi siatti
([11]).
E opportuno iniziare lo studio degli accrescimenti nali a partire da quello piu semplice
essendo inoltre possibile trattare i processi complessi come somma di quelli piu elementari.
La risposta termica di una nana in accrescimento di materia con le modalita sopra descritte e il risultato nale di tale accrescimento saranno l'oggetto di indagine dei paragra
che seguono.
2.7.1 Strutture Stellari Degeneri di C-O in Accrescimento di
C+O
Come di norma, anche nel caso di accrescimento di carbonio ed ossigeno su una nana di
C-O, esistono dei valori limite di M_ (M_ Edd ) al di sopra dei quali non e possibile depositare
la materia trasferita sulla nana che dovrebbe accrescerla. Quando invece l'accrescimento
procede su tassi piu bassi la materia viene accettata ed e resa disponibile per liberare
energia gravitazionale in virtu del riassestamento strutturale cui va soggetta la nana bianca
in aumento di massa. Tale energia e stimabile dalla relazione per l'energia potenziale
gravitazionale
GM 2
U=
(2.14)
R
derivando ed assumendo una relazione massa-raggio del tipo M const=R3 , si ottiene
7GM M_
U_ =
(2.15)
3R
Il tempo-scala tipico nel quale negli strati piu esterni si libera energia di riscaldamento
compressionale (rc) e dato, in accordo con [9], da:
ÆM
rc = _
(2.16)
M
dove ÆM rappresenta la quantita di massa compresa in una altezza scala di pressione Hp .
L' energia liberata dal riscaldamento compressionale della materia accresciuta puo essere
diusa anche agli strati piu interni della struttura su tempi scala di diusione denibili,
in accordo con [9], dalla relazione:
diff =
Cp2 Hp2
acT 3
(2.17)
49
2.7. Gli Accrescimenti Finali
Fig. 2.2: Come si modica nel tempo la struttura interna (nel piano T ) di una nana di C-O di massa
iniziale di 0:8M accrescita con carbonio ed ossigeno ad un tasso M_
= 10 5Myr 1. La curva piu
fredda e meno densa e quella piu prossima al modello iniziale. Il luogo dove si innescano le reazioni di
termofusione del carbonio (C-ignition) e evidenziato con un punto spesso.
CO
dove Cp e il calore specico ed Hp l'altezza scala di pressione, mentre gli altri simboli
hanno il signicato usuale. Il tempo-scala di trasferimento dell'energia diff dipende
soltanto dalle proprieta strutturali della stella che accresce massa (che possono comunque
modicarsi durante il processo di crescita di massa) mentre rc dipende principalmente da
M_ . Pertanto, se l' accrescimento avviene su tempi-scala rapidi (M_ elevati ma comunque
inferiori a M_ Edd ) si avra che normalmente rc < diff per cui non ci sara tempo per diffondere alla parte rimanente della struttura l' energia depositata negli strati esterni nei
quali si registrera un aumento della temperatura no all' innnesco locale delle possibili
reazioni nucleari di fusione. Se invece l'accrescimento procede con M_ piu bassi allora si
avra che diff < rc per cui tutta la struttura potra andare soggetta ad un generale riscaldamento. In questo caso l'eventuale innesco di reazioni di termofusione si verichera nelle
zone centrali. In ogni caso, perche la massa accresciuta porti ad un aumento di energia
(localizzato oppure generalizzato) e comunque necessario che l' energia compressionale di
accrescimento superi le perdite per irraggiamento e neutrini. Nel caso presente questa
condizione si verica per valori di M_ maggiori di 5 10 10 M yr 1.
Durante la fase di accrescimento, a seguito del riaggiustamento strutturale della nana
bianca che acquisisce massa, sia diff che rc potranno variare i loro valori determinando
degli andamenti i cui dettagli sono diÆcilmente valutabili a priori.
50
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
M_ C +O
M_ Edd > M_ > 5 10
5 10
10
6
< M_ < 5 10
6
Eetti dell' Accrescimento
Risultato Finale
innesco di C in shell
formazione di nana di O-Ne
innesco centrale di C
deagrazione del C
Tab. 2.2: Eetti dell'accrescimento di C+O su nane di CO al variare di M_
CO
.
Esperimenti numerici in cui una miscela composta da carbonio ed ossigeno viene fatta
accrescere su una nana di C-O sono stati condotti da diversi autori (per esempio [8] e
[10]). I risultati sono tra loro in buon accordo e sono sintetizzabili come segue:
Il primo caso (rc < diff ) si verica quando M_ Edd > M_ CO > 5 10 6 . Durante una fase
di accrescimento di C+O con tassi all' interno di questo intervallo la temperatura degli
strati esterni cresce molto velocemente. Il massimo di temperatura si localizza in un punto
la cui posizione dipende da M_ ed e tanto piu esterno quanto maggiore e M_ . Quando la
temperatura supera localmente 4 5 108 K (il valore preciso dipendendo da e dall'
abbondanza di nuclei di carbonio) si innescano le reazioni di termofusione del carbonio in
shell. L' innesco e tanto piu lontano dall' assumere l' aspetto di un ash dinamico quanto
piu superciale e la posizione del massimo di temperatura. Il bruciamento, una volta
raggiunto un regime locale di stazionarieta, inizia a propagarsi lentamente verso il centro
lasciando alle proprie spalle materia composta essenzialmente di ossigeno e neon. Tutta
la nana di C-O e inne trasformata in una nana di O-Ne. In gura 2.2 sono riportate
nel piano T diverse strutture interne, a tempi diversi, di modelli in accrescimento
di carbonio ed ossigeno con M_ CO = 10 5 M yr 1 e massa iniziale della nana di C-O di
0:8M . Il modello piu prossimo a quello iniziale e quello piu fredddo e meno denso, il
centro della struttura si trova sul lato destro. Si nota come per questi valori del tasso di
accrescimento vengano subito riscaldate le zone esterne e come tale processo prosegua con
continuita no a che non si verichi un innesco delle reazioni del carbonio in una zona
esterna prima che questo possa accadere in altra parte della struttura.
Una situazione diversa si verica quando l'accrescimento procede con tassi 5 10 10 <
M_ CO < 5 10 6 . In questo caso si ha che diff < rc per cui l'energia compressionale
di accrescimento si puo liberamente ridistribuire su tutta la struttura determinando un
aumento generalizzato di temperatura seppure a tassi locali che sono evidentemente piu
bassi di quello registrabile nel caso precedente in prossimita della superce. La soglia di
51
2.7. Gli Accrescimenti Finali
Fig. 2.3: Come si modica nel tempo la struttura interna (nel piano T ) di una nana di C-O di massa
iniziale di 0:8M accrescita con carbonio ed ossigeno ad un tasso M_
= 10 8Myr 1. La curva piu
fredda e meno densa e quella piu prossima al modello iniziale. Il luogo dove si innescano le reazioni di
termofusione del carbonio (C-ignition) e evidenziato con un punto spesso.
CO
52
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
temperatura per l' innesco delle reazioni del carbonio viene raggiunta al centro quando la
massa totale approssima la massa di Chandraseckar. Quest' ultima condizione discende
dalle proprieta delle strutture stellari degeneri di essere tanto piu comprimibili quanto
piu si avvicinano alla massa critica. La gura 2.3 riporta un esempio di accrescimento
come quello appena descritto. Si tratta di una nana dalle caratterisitche iniziali identiche
a quella dell'esperimento numerico riportato in g. 2.2 ma con un accrescimento di C+O
ad un tasso M_ CO = 10 8 M yr 1. La curva tratteggiata descrive l' evoluzione del centro
della struttura. A parte un riscaldamento iniziale delle zone esterne, si nota come molto
presto l'energia venga trasferita alle zone centrali e come siano solo queste quelle soggette
ad un forte riscaldamento nale. L'innesco centrale di carbonio in una nana di C-O di
massa prossima a quella di Chandraseckar costituisce un evento di importanza primaria
nello studio dei fenomeni esplosivi. Il profondo stato di degenerazione della materia
implica, in forza dell' aspetto assunto dall' equazione di stato in questa condizione, che
ad un aumento di temperatura non segue alcun riaggiustamento strutturale tendente
all' autoregolamentazione del bruciamento. Cresce, invece, in un processo reazionato
positivamente, la quantita di energia prodotta che a sua volta induce un ulteriore aumento
di temperatura. Tutto il processo, che porta alla totale distruzione della nana di C-O,
verra discusso in dettaglio in un successivo paragrafo di questo capitolo.
2.7.2 Strutture Stellari Degeneri di C-O in Accrescimento di He
Si e avuto modo di vedere, nei paragra che precedono, come sia possibile che una nana
di C-O possa essere soggetta ad accrescimento di He da parte di una compagna che puo
assumere un aspetto strutturale degenere oppure essere in una fase normale di bruciamento
centrale di He. Mentre nel secondo caso il tasso di trasferimento di massa puo essere
ragionevolmente stimato, nel caso in cui sia una nana di He a trasferire massa tale stima
e ancora di diÆcile attuazione. Si e anche avuto modo di vedere come possa determinarsi
una situazione nale in cui sia una nana di He ad essere accresciuta di He. Quest' ultima
fenomenologia, che puo pure rivelarsi di una certa importanza in taluni casi specici, non
verra tuttavia discussa in questo libro.
Anche in questo caso aronteremo l' analisi della risposta termica della struttura
stellare degenere di C-O soggetta ad accrescimento, parametrizzando i valori del tasso
di accrescimento di He. Come nel caso discusso nel paragrafo che precede, esistono, all'
interno del range dei valori di M_ per i quali la materia viene eettivamente depositata
sulla nana di C-O, dei valori del tasso di accrescimento per i quali si registra una crescita
globale della temperatura dell'intera struttura. Per altri valori del tasso di accrescimento,
invece, saranno precipuamente soggetti a riscaldamento i soli strati esterni. Infatti, in
quest'ultimo caso si ha che rc < diff , per cui non c'e tempo di diondere a tutta la
struttura gli eetti indotti dal deposito di energia negli strati esterni.
E necessario precisare immediatamente che non sara mai possibile che le prime rezioni
2.7. Gli Accrescimenti Finali
53
Fig. 2.4: Eetti dell'accrescimento di He (Y=0.98, Z=0.02) ad un tasso come dato in ordianta (in M
yr 1 ) su una nana di C-O di massa come data in ascissa (in M ).
nucleari ad essere innescate siano quelle del carbonio al centro o in altra parte del nucleo
di C-O, qualunque sia il tasso di accrescimento assunto. Questo per la semplice ragione
che la soglia di temperatura per innescare le reazioni 3 (T 108 K ) e molto piu bassa di
quella necessaria per innescare le reazioni di termofusione del carbonio (T 5 108 K ).
Prima che quest' ultima temperatura possa venire raggiunta in una qualche parte del
nucleo di C-O la prima verra sicuramente superata nel mantello di He.
Gli esperimenti numerici, [14], mostrano che per valori di M_ He compresi tra M_ He 5 10 10 M yr 1 e M_ He 10 6 M yr 1 si verica comunque un innesco in shell delle
reazioni di fusione 3. Per valori di M_ He rispettivamente inferiori o superiori a questi
si registrera, rispettivamente, un rareddamento globale della struttura oppure una espansione incondizionata degli strati esterni (si veda la g. 2.4). I valori limite citati di
M_ He dipendono anche, seppure moderatamente, dalla massa iniziale della nana di C-O
come mostrato in g. 2.4, ma anche dal suo stato termico iniziale. All' interno del range
di valori di M_ He per i quali si verica l'innesco delle reazioni di termofusione dell'elio
nello strato esterno di He, bisognera tuttavia distinguere due casi i cui risultati nali
dieriscono nettamente.
Per valori di M_ He compresi tra 3 10 8 M yr 1 e 10 6 M yr 1 si rientra, in
media, nella condizione rc < diff . Per tale ragione l' energia liberata dalla materia accresciuta viene in massima parte trattenuta localmente negli strati esterni dove si sviluppa
immediatamente un sensibile aumento di temperatura. La gura 2.5, ([16]), riporta i risul-
54
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.5: Andamenti strutturali a vari tempi evolutivi di una nana di C-O che accresce He ad M_ come
dato in gura. In questo caso per cui si riscaldano solo gli strati estrni ed il bruciamento
dell'elio viene innescato in una zona molto superciale. Il risultato e un ash debole.
He
rc
dif f
tati di un esperimento numerico che rientra nei parametri in discussione. La soglia per
l'innesco delle reazioni di termofusione dell'elio viene presto superata localmente in regioni
esterne, lontane dalla base dell'inviluppo di He, di densita relativamente bassa. Per questi
parametri l' innesco dell'He, sebbene assuma comunque l'aspetto di un ash, non produce
un evento dinamico. Questo tipo di evento puo essere seguito attraverso l'utilizzo di un
codice idrostatico di evoluzione stellare per tutto il suo svolgimento. Il risultato nale
e quello di aver trasformato in C+O tutta la materia precedentemente accresciuta sotto
forma di He. Questo evento comporta, in denitiva, un accrescimento indiretto del nucleo
di C-O le cui conseguenze sono riconducibili a quelle enunciate nel paragrafo precedente.
Occorre tuttavia tenere presente che, a seguito dell'innesco dell' elio, gli strati esterni
subiscono una forte espansione che non avrebbe conseguenze se la nana che subisce il ash
fosse isolata. Tuttavia ci si deve aspettare che, nel mondo reale, l'espansione degli strati
esterni porti ad una interazione di questi con la compagna che sta cedendo massa e quindi
ad una situazione di presumibile Common Envelope. Gli eetti di tale interazione potrebbero quindi essere quelli di disperdere nello spazio che circonda il sistema binario buona
parte dello strato di He precedentemente accresciuto. In questo contesto appare diÆcilmente ipotizzabile che la nana di C-O possa accrescere la propria massa con i prodotti
della combustione dell'elio e raggiungere valori prossimi a quella di Chandrasechkar se
non nel caso di ashes dell' elio molto poco energetici, ovvero per un ristretto range di
55
2.7. Gli Accrescimenti Finali
Fig. 2.6: Andamenti strutturali a tempi diversi di una nana di C-O che accresce He con parametri
come dati in gura. Sono indicati, con curve tratteggiate, le posizioni del centro e della base dello strato
esterno di He venutosi a creare a seguito dell'accrescimento. In questo caso per cui tutta
la struttura va soggetta a riscaldamento. Tuttavia, come descritto nel testo, le prime reazioni nucleari
ad innescarsi saranno le 3 alla base dell'inviluppo di He ed il risultato sara un evento esplosivo tipo
sub-Chandrasekhar.
dif f
rc
valori di M_ He intorno a 10 7 M yr 1 .
Una situazione diversa si incontra quando 5 10 10 < M_ He (M =yr) < 3 10 8 . In
questo range di valori di M_ He si ha che rc > diff per cui tutta la struttura va soggetta ad
un riscaldamento generalizzato come risulta chiaramente osservabile da un'analisi della g.
2.6 ([16]). Il minore tasso specico con cui l'energia di accrescimento viene depositata,
aggiunto al fatto che questa viene ridistribuita su di una quantita maggiore di massa,
implica che prima che venga raggiunta la soglia di innesco delle reazioni di fusione dell'elio
debba venir accresciuta una quantita di He ragionevolmente alta (MHe > 0:2M ). Al
crescere della quantita di massa accresciuta la posizione sica della base dello strato di
He si sposta a densita sempre piu alte. (Infatti la sua posizione relativa diviene sempre
piu interna). D'altronde, la base sica dello strato di He e il posto dove per prima
verra raggiunta la temperatura di innesco delle reazioni di termofusione dell'elio. Ne
consegue che, al momento dell' innesco, le reazioni di termofusione si svilupperanno in
un ambiente degenere producendo un ash molto energetico che puo portare di fatto ad
un evento esplosivo (si noti il prolo della temperatura nell'ultimo modello illustrato in
g. 2.6). Si deve notare come per ottenere un innesco degenere del tipo di quello appena
descritto, che risulta essere particolarmente energetico, non sia necessario raggiungere la
56
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
massa di Chandrasekhar. Per questa ragione e invalso l'uso di denominare questa classe
di eventi come sub-Chandrasekhar. Le modalita con le quali si sviluppa l' esplosione ed
il risultato nale di questa saranno analizzate in un successivo paragrafo.
E molto importante fare presente che i calcoli evolutivi relativi alle fasi nali di trasferimento di He da parte di una stella di elio (ancora in fase attiva di bruciamento centrale
3) su di una nana di C-O hanno mostrato che il tasso di accrescimento che si ottiene
rientra esattamente nel range di valori per i quali ci si attende un evento esplosivo tipo
sub-Chandrasekhar ([14]). Qualora la componente che cede He assuma invece l'aspetto
di una struttura degenere, il reale tasso di trasferimento di massa non e facilmente determinabile per cui rimane possibile il vericarsi di una varieta di eventi all'interno delle
fenomenologie appena descritte.
2.7.3 Strutture Degeneri di C-O soggette ad accrescimento di
H
Il processo di trasferimento di idrogeno da parte di una stella di Sequenza Principale (o di
ramo di gigante) su una nana bianca e stato invocato per spiegare una varieta di fenomeni
astrosici. Seguendo le linee concettuali impostate all' inizio di questa sezione potremo
aermare che si tratta di un processo che prende corpo in un sistema binario di basso
livello di esoticita. Il sistema tipico in cui il processo si verica si trova ad uno stadio
evolutivo complessivo solo mediamente avanzato. La nana e il prodotto evolutivo nale
della primaria (a seguito di un episodio di common envelope), mentre la secondaria ha
appena iniziato ad evolvere. Anche dal punto di vista teorico l' esistenza di un sistema
binario siatto e facilmente giusticabile, specialmente se non si pretende di determinare
con assoluta precisione i parametri del sistema intermedio a partire dai parametri del
sistema originario. Gli eetti prodotti dall'accrescimento di H sulla struttura degenere
di C-O sono invece piu complessi di quelli descritti nei casi precedenti, quando si sono
studiati gli accrescimenti su una nana di C-O di materia nuclearmente piu evoluta dell'
idrogeno
Come di norma, il parametro guida che determina il tipo di eetto indotto dal trasferimento di massa sulla nana bianca e il tasso di accrescimento M_ H . La maggiore dierenza,
rispetto ai casi che precedono, consiste nel fatto che nel caso di accrescimento di idrogeno
non esiste nessun valore di M_ H per il quale si registri come unico eetto un incremento
generale della temperatura nella totalita della struttura in accrescimento. Questo perche
le reazioni di combustione dell' idrogeno vengono innescate a temperature relativamente
basse, evento che si verica prima che l' energia termica depositata nelle zone esterne da
parte della materia in accrescimento possa essere trasferita al resto della struttura.
Prescindendo momentaneamente dal caso in cui la materia accresciuta si dispone su
una congurazione espansa, tipica di una gigante rossa, si ha che l' idrogeno accresciuto
2.7. Gli Accrescimenti Finali
57
Fig. 2.7: Eetti dell' accrescimento di materia ricca di idrogeno (X=0.7) con metallicita Z=0.02 su di
una nana bianca di C-O di massa come data in ascissa in M. I valori in ordinata sono in Myr 1 .
potra essere bruciato, al variare di M_ H , attraverso una serie di pulsi ricorrenti di combustione oppure in modo stazionario, allo stesso tasso con cui la materia viene eettivamente
accresciuta. L' energia dei pulsi di combustione dell'idrogeno dipende anch' essa da M_ H .
Al decrescere del tasso di accrescimento i pulsi divengono sempre piu energetici passando
da un aspetto non-dinamico ad uno esplosivo tipo \nova".
La gura 2.7, ([16]), fornisce una descrizione del tipo di evento che segue all' accrescimento di idrogeno di ssato M_ H (in ordinata) al variare della massa della nana bianca
di C-O soggetta ad accrescimento (in ascissa). I valori riportati in gura si riferiscono a
materia con contenuto chimico di tipo solare (Z = 0:02 e Y = 0:28). Si puo osservare
come in eetti il valore della massa della nana bianca costituisca un secondo parametro
non trascurabile nel determinare l'eetto indotto dall'accrescimento. Qualora durante
il processo di accrescimento venga oltrepassato uno dei bordi riportati schematicamente
in g. 2.7 per separare le diverse zone d'interesse, a causa, per esempio, del crescere
della massa della nana in accrescimento, si verichera rapidamente una variazione della
tipologia del bruciamento di idrogeno.
Il processo di bruciamento dell'idrogeno attraverso pulsi ricorrenti di combustione
costituisce un evento di rilevante interesse la cui importanza sara chiara dalle descrizioni
che seguono. Attraverso questo processo, di cui il bruciamento stazionario costituisce
un aspetto particolare, si sintetizza materia ricca di elio (Y 0:98) con la quale viene
58
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.8: Evoluzione sul piano HR di una struttura di C-O degenere in accrescimento di H durante un
tipico pulso di combustione dell'H. Sono indicati i punti di minimo e massimo usso di energia dovuta
alle reazioni di bruciamento dell'idrogeno ( ) ed a quelle, molto meno intense, di bruciamento dell'elio
nella shell sottostante ( ). Sono anche riportati i punti di inizio (IC), massima estensione (Max C)
e ne (FC) della convezione che si instaura nello strato di idrogeno a seguito dell'innesco delle reazioni
di termofusione dell'H.
H
He
accresciuto il nucleo di C-O riconducendo il problema, seppure con qualche variante, al
caso descritto nel paragrafo precedente.
Durante un pulso la struttura descrive nel diagramma HR un ciclo le cui proprieta
dipendono sia dal valore di M_ H sia dalla massa del nucleo di C-O (ma anche dal contenuto di metalli della materia accresciuta). La gura 2.8 riproduce il ciclo percorso nel
diagramma HR durante un tipico pulso da una nana di C-O di massa 0:523M soggetta
ad un accrescimento costante di idrogeno con M_ H = 10 8 M yr 1. La porzione di ciclo
riprodotta con un tratto di curva piu marcato corrisponde ad una fase evolutiva in cui
quasi tutta l'energia liberata deriva dal bruciamento di idrogeno (LH =Ltot 1). Durante
questa fase la shell di idrogeno avanza in massa verso l'esterno con una certa rapidita lasciando alle proprie spalle i prodotti di combustione che accrescono la massa dello strato
di He che si viene a creare tra il nucleo di C-O e la materia ricca di H che viene accresciuta dalla compagna. Questa proprieta e anche riscontrabile nel pannello a della
gura 2.9 notando anche, dal pannello b della stessa, che in questo tratto H = LH =Ltot
e prossimo ad 1 (H e il usso relativo di energia dovuto alle combustioni di idrogeno).
Si noti come nella g. 2.9 la variabile indipendente, essendo rappresentata dalla massa
il cui valore cresce linearmente con il tempo, sia, in denitiva, il tempo. Quando la shell
2.7. Gli Accrescimenti Finali
59
di H raggiunge gli strati piu esterni la sua temperatura inizia a diminuire drasticamente
(pannello c della gura 2.9). L' aumento di densita (pannello e di g.2.9) non riesce a
contenere a livelli ragionevoli la produzione di energia nucleare che, come mostrato nel
pannello b della stessa gura, diminuisce drasticamente. Si noti come la produzione di
energia gravotermica (gr ) si sostituisca immediatamente a quella nucleare. Inizia una
fase di rareddamento della struttura la cui unica fonte energetica e rappresentata dalle
riserve termiche disponibili e dal riassestamento strutturale della massa che nel frattempo
continua ad essere accresciuta sulla supercie della nana bianca. Si noti come durante
questo periodo la posizione in massa della shell di H rimanga immutata mentre la massa
totale continui a crescere costantemente (pannello a di g. 2.9).
Se non ci fosse un continuo apporto di massa il destino di questa struttura sarebbe
segnato da un rareddamento continuo, da H tendente monotonamente a zero e da
gr tendente a 1. Invece, la massa accresciuta con continuita, e resa disponibile per
essere compressa gravitazionalmente, determina un' evoluzione diversa e induce presto
una inversione nell' andamento della temperatura della shell di H che inizia a crescere
nuovamente, inducendo anche una netta risalita del usso dovuto alla combustione di
idrogeno (pannelli b e c). Si noti come la maggior quantita di massa accresciuta durante
il ciclo sia da registrarsi proprio in questa fase di bassa luminosita (pannelli a e d di g.
2.9). La densita in continua crescita e l' aumento netto di temperatura determinano una
crescita quasi incondizionata delle reazioni nucleari che inne conferiscono al bruciamento
nucleare l'aspetto di un ash. In realta, nella shell di idrogeno non sono presenti condizioni
di degenerazione elettronica tali da indurre la formazione di un ash nella forma classica
in cui questo si intende (si veda, per esempio, il ash dell' elio nel nucleo di giganti rosse di
piccola massa). Il motivo per cui le reazioni nucleari assumono un andamento rapidamente
crescente va invece ricercato nel valore assunto dal tempo-scala di trasferimento dell'
energia generata alla base dell'inviluppo di idrogeno. Questo assume valori piu elevati
del tempo-scala su cui cresce la produzione di energia. Si instaura immediatamente un
trasporto di tipo convettivo che molto rapidamente viene ad interessare tutto l'inviluppo
di idrogeno. Gli strati esterni espandono su tempi scala termici inducendo una forte
diminuizione di densita ed una prima sostanziale riduzione della temperatura alla base
dell'inviluppo di idrogeno (pannelli c ed e di gura 2.9), mentre un usso sempre maggiore
riesce ad essere trasferito alla supercie inducendo un aumento di luminosita (pannello d
della stessa gura). In gura 2.8 il punto di inizio della convezione e contrassegato con
IC mentre con Max C lo e quello in cui la convezione raggiunge la supercie. Tutta la
fase di espansione e di riaggiustamento strutturale che segue all'innesco veemente delle
reazioni nucleari di termofusione dell'idrogeno, e identicabile in g. 2.8 con tutta la parte
destra del ciclo no al massimo di luminosita, a basse temperature eettive, dove di nuovo
H 1. Si deve notare come durante tutta la fase veloce di espansione e riassorbimento
del ash la shell di H non sia avanzata in massa nonostante l' elevata eÆcienza raggiunta
60
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
qui dalla combustione (H = LH =Ltot > 100). Questo e dovuto ai tempi molto brevi in
cui si svolge questa parte di ciclo. Quando il bruciamento di H diviene di nuovo stabile i
tempi evolutivi tornano a crescere (tempi scala nucleari) e la shell comincia di nuovo ad
avanzare. I prodotti della combustione accrescono in massa lo strato di He che la separa
dal nucleo di C-O. Il livello massimo di luminosita raggiunto durante il ciclo dipende
esclusivamente dalla massa del nucleo stellare sottostante la shell di H con il quale, come
di norma, la shell interagisce determinando la ben nota relazione Mcore L (massa di core
- luminosita superciale) valida in presenza di un nucleo stellare degenere e di una shell
in bruciamento stazionario.
Quanto discusso e riferibile a tutti i modelli che insistono nell'area che in gura 2.7
viene contrassegnata con la dizione Pulsi Deboli. Nei modelli che si trovano invece nella
regione Pulsi Forti della stessa gura si deve registrare un evento di innesco delle reazioni
di termofusione dell'idrogeno condizionato anche da un livello non trascurabile di degenerazione. Si deve presumere che in questi casi l'equilibrio idrostatico non venga conservato
a lungo e che l'evento determini anche l' espulsione di parte dell'inviluppo precedentemente accresciuto, se non di tutto. Si ritiene che in questi casi l'evento che si produce sia
riconducibile a quello che osservativamente viene cotrassegnato con il nome di \Nova".
Si puo immediatamente comprendere come sia anche possibile l'esistenza di tassi di
accrescimento che comportano un bruciamento contestuale della materia accresciuta se
si considera che nella zona in cui H 1 si possa depositare materia allo stesso tasso
con cui questa viene bruciata e convertita in elio. Questa condizione e contrassegnata in
gura 2.7 con la dizione Accrescimento Stazionario.
Quando invece l' accrescimento prosegue con tassi che superano il massimo tasso di
avanzamento consentito alla shell di H si ha che la massa dell'inviluppo di H non puo fare
altro che aumentare. Si determina cos una condizione tipica di una struttura di gigante
rossa (o meglio di stella di AGB). Questo succede ancor prima che M_ superi M_ Edd ed
e determinato dal limite sico imposto dal nucleo stellare alla shell di H in termini di
richiesta di luminosita. In altri termini, quando il pulso ha termine e H e di nuovo
1 la luminosita del modello e determinata dalla massa del nucleo e non puo essere
superiore. Soddisfare una richiesta specica di luminosita (e non di piu) vuol dire, per la
shell, bruciare (ovvero avanzare) non piu di quanto richiesto, cioe, ad un tasso M_ H shell
che e funzione soltanto di Mcore . Se avviene che M_ H > M_ H shell allora l'inviluppo di H
cresce indenitamente e la struttura diviene una gigante rossa.
Tutte le tipologie descritte precedentemente, in relazione alle modalita di combustione
dell'idrogeno sulla supercie di una nana bianca in accrescimento, comportano, in denitiva, un accrescimento di He sul nucleo di C-O come prodotto di combustione dell'idrogeno.
(Fatta forse eccezione per la tipologia relativa ai Pulsi Forti poiche in questo caso, a
seguito dell'innesco degenere dell'idrogeno, potrebbe vericarsi la perdita degli strati
esterni precedentemente accresciuti durante la fase quiescente del pulso.) Sarebbe ra-
2.7. Gli Accrescimenti Finali
61
Fig. 2.9: Variazioni in funzione del tempo (in realta in funzione della massa totale che cresce linearmente nel tempo) di grandezze siche caratteristiche, durante due episodi di bruciamento impulsivo dell'
idrogeno, in un modello di nana di C-O in accrescimento di H come specicato nel testo. Pannello a):
valore della massa totale (linea tratteggiata) e posizione in massa della shell di H (punto di massima
produzione nucleare). Pannello b): luminosita dovuta al bruciamento di idrogeno e luminosita di origine
gravo-termica (ambedue in unita della luminosita superciale). Pannelli c) ed e): logaritmi della temperatura (in K) e della densita (in gr cm 3 ) nella shell di H. Pannelli d) ed f): logaritmi della luminosita
superciale e del raggio (ambedue in unita solari).
62
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.10: Andamento, nel piano T , dei valori interni di densita e temperatura di due strutture degeneri
di C-O di egual massa iniziale e di massa istantanea identica (come dato in gura) accresciute con He allo
stesso tasso di accrescimento (anch'esso dato in gura) in un caso come prodotto di combustione dell'H
(linea continua), nell'altro direttamente con materia ricca di He (linea tratteggiata). Le frecce indicano
la posizione delle shells di He e di quella di H nel primo modello. Lo spessore in massa dello strato di
He e confrontabile essendo estremamente ridotta la massa dell'inviluppo di H nel primo caso.
gionevole supporre, dunque, che per conoscere gli eetti evolutivi a lungo termine di nane
che accrescono H sia possibile ricondursi ai risultati del paragrafo precedente relativo
all'accrescimento di He. Questo non e di fatto possibile. Infatti la presenza della shell
di H determina una variazione delle proprieta siche della sottostante shell di He che la
rendono piu calda a parita di M_ He .
Questa proprieta e chiaramente illustrata dalla g. 2.10, (tratta da [12]), dove vengono
riportate, allo stesso tempo evolutivo (quindi alla stessa massa istantanea), le strutture
interne (nel piano T ) di due nane di C-O con stessa massa iniziale in cui il risultato
dell'accrescimento e stato quello di formare uno strato di elio intorno al nucleo di C-O. In
pratica ambedue hanno accresciuto He con lo stesso tasso M_ He pero, in un caso attraverso
l'intermediazione di una shell di combustione di idrogeno (curva a tratto continuo), nell'
altro (curva tratteggiata) direttamente con materia ricca di He (Y = 0:98; Z = 0:02). Si
deve far notare che nel primo caso la massa dell'inviluppo di H ha un valore trascurabile
per cui gli strati di He si possono considerare, in pratica, di egual massa. Nel primo caso lo
strato ricco di He risulta essere, a pari densita, nettamente piu caldo. Di conseguenza, le
temperature necessarie per innescare le reazioni di fusione 3 saranno raggiunte prima, ed
avendo accresciuto una massa minore, rispetto a quanto non sia richiesto dal modello che
2.7. Gli Accrescimenti Finali
63
accresce He direttamente. Questo comporta un ash dell' He molto meno energetico. Nei
fatti, un innesco fuori centro delle combustioni 3, che nel caso di accrescimento diretto di
He puo portare ad un evento esplosivo (come descritto nella seconda meta del paragrafo
precedente), quando si accresce He indirettamente, sebbene allo stesso M_ He , porta ad un
ash debole riassorbibile non dinamicamente dalla struttura.
La proprieta appena descritta sembrerebbe indicare che, partendo da accrescimenti di
H, non appare possibile pervenire ad inneschi dell'elio che comportino eventi esplosivi denominati precedentemente del tipo sub-Chandrasekhar. Sembrerebbe invece possibile che,
attraverso una serie ripetuta di ashes deboli dell'elio, il nucleo di C-O possa venire accresciuto in massa di C+O (prodotto di combustione dell'He) no al raggiungimento della
massa di Chandrasekhar. Tuttavia, nel paragrafo che segue si vedra come la prima evenienza (divieto di sub-Chandrasekhar) comporti delle eccezioni e come la seconda (Chandrasekhar) risulti, di fatto, di diÆcile conseguimento.
2.7.4 Eetti a lungo termine dell'accrescimento di H su nane di
C-O
La gura 2.11 (da [13]) fornisce una descrizione sintetica di quanto esposto nel paragrafo
precedente. Si tratta di risultati di esperimenti numerici in cui nane di C-O di masse
iniziali di 0:516, 0:8 e 1:0M sono state accresciute con materia ricca di idrogeno (X =
0:7; Y = 0:28 e Z = 0:02) ad un tasso M_ H come riportato in ordinata (in M yr 1) che e
stato mantenuto costante durante ogni singolo esperimento. Si puo notare come esistano
casi di accrescimento in cui l'idrogeno bruci stazionariamente (la crescita di massa viene
riportata con un tratto continuo) e casi in cui il bruciamento avviene tramite pulsi (la
crescita di massa viene riportata con un tratto a dente di sega). In ambedue i casi l'eetto
della combustione e quello di far cresce la massa dello strato di He a ridosso del nucleo di
C-O. Occorre citare il fatto che durante il bruciamento di idrogeno, la combustione dell'elio
assume valori molto ridotti sebbene crescenti nel tempo ma tali, comunque, da non indurre
nucleosintesi rilevante. La combustione dell'elio diventa invece dominante quando alla
base dello strato di He (shell di He) viene raggiunta la temperatura di 108 K e quando
questo succede l'innesco delle 3 assume l'andamento tipico di un ash. L'innesco dell'He
in shell e riportato in gura con il simbolo . Nella maggioranza dei casi il ash dell'elio
e di tipo \non-dinamico" e puo essere seguito facilmente con i programmi di calcolo
descritti nei capitoli precedenti. Anche nel caso dell'innesco dell'elio in shell si registra la
formazione immediata di una shell convettiva subito sopra la zona di bruciamento 3 per
trasportare il surplus di energia prodotta. Se il ash e particolarmente energetico (basse
masse iniziali della nana di C-O) la convezione riesce a penetrare l'inviluppo di idrogeno
deducendo protoni in zone a temperatura molto elevata e determinando l'insorgere di
situazioni complesse la cui descrizione esula dagli scopi di questa trattazione. Per masse
64
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.11: Conseguenze dell'accrescimento di H ai tassi indicati in ordinata (in M yr 1 ) su nane
bianche di C-O di massa come in ascissa. Nel riquadro e nel testo vengono chiariti i signicati dei vari
simboli riportati in gura. Le tre linee rette separano le varie zone in cui si divide il piano in base al tipo
di risposta all'accrescimento come dato in g. 9.
iniziali piu elevate (M 0:8M ) la convezione rimane limitata dentro lo strato di He.
In ogni caso l'innesco dell'elio induce una notevole espansione di tutti gli strati esterni
(mantello di H e strato di He). Questa proprieta comporta la formazione di un ulteriore
episodio di Common Envelope con la conseguenza che una parte rilevante dello strato di
He e tutto il mantello di H vanno dispersi nello spazio, non contribuendo, in denitiva,
ad accrescere in massa il nucleo di C-O.
Sembrerebbe quindi plausibile concludere che l'accrescimento di H, oltre a risultare ineÆcace per la produzione di scenari esplosivi del tipo sub-Chandrasekhar, non e eÆcace
neanche nell'aspetto di consentire al nucleo di C-O di raggiungere la massa di Chandrasekhar. Tuttevia, a questo quadro si ammettono due eccezioni che si vericano per
valori estremi dei parametri M_ H e massa iniziale della nana bianca MW D;0 .
L'esistenza di una prima eccezione e deducibile da una analisi della gura 2.11. Per
masse iniziali della nana di C-O dell'ordine di MW D;0 0:5 0:7M e per tassi di accrescimento M_ H 1 2 10 8 M yr 1, il ash dell' He viene raggiunto dopo che 0:2M
di H sono state accresciute e convertite in He attraverso bruciamenti nucleari pulsanti
di H. Dalla stessa gura e possibile dedurre come, per bassi valori di MW D;0 e per tassi
di accrescimento all'interno della zona \Pulsi Deboli", la quantita di materia accresciuta
prima dell'innesco del ash dell' He cresca, al decrescere di M_ H , piu che proporzional-
2.8. Inneschi Termonucleari a Carattere Esplosivo
65
mente. Questo andamento e ascrivibile al fatto che in queste strutture, da un certo istante
evolutivo in poi, diventa trascurabile l'eetto che la shell di H induce su quella di He nel
renderla piu calda e meno densa. In pratica, per questi modelli gli eetti indotti dal
processo di accrescimento di He in forma diretta divengono confrontabili con quelli determinati dall'accrescimento di He attraverso i prodotti di combustione dell'idrogeno. Piu
semplicemente, i naturali tempi lunghi del fenomeno comportano una ulteriore dilazione
dei tempi evolutivi in virtu del fatto che la shell di He diviene, per cos dire, disaccoppiata
termicamente dagli strati superciali a causa della lontananza in massa di questi ultimi.
Nei fatti, il modello con MW D;0 = 0:516M e M_ H = 2 10 8M yr 1, produce un innesco
eplosivo delle reazioni 3 che conduce ad un evento del tipo sub-Chandrasekhar.
Una seconda eccezione si puo vericare per valori molto alti di MW D;0 ( 1:3M ).
Qualora nane bianche di C-O di massa iniziale cos elevata fossero realmente prodotte in
natura, l'accrescimento di H a tassi di M_ H 10 6 M yr 1 produrrebbe un bruciamento
stazionario dell'H e ashes dell'elio molto poco energetici. In tal caso, all'innesco di
ogni ash dell'elio si vericherebbe una perdita di massa trascurabile o nulla, aspetto che
comporta un rapido raggiungimento della massa critica di Chandrasekhar nel il nucleo di
C-O e, quindi, un innesco centrale esplosivo delle reazioni di termofusione del carbonio.
Mentre l'esistenza della prima eccezione ha ricevuto una conferma teorica esplicita,
l'esistenza della seconda deve essere ancora vagliata in vari punti, principalmente in quello
che prevede la formazione di una nana di C-O particolarmente massiccia.
2.8 Inneschi Termonucleari a Carattere Esplosivo
Nei due paragra che seguono vengono analizzati in dettaglio i due inneschi termonucleari a carattere esplosivo meglio conosciuti. Si tratta dell'innesco degenere centrale delle
reazioni di termofusione del carbonio e di quello, sempre degenere, delle reazioni 3 alla
base di una shell di He relativamente massiccia che circonda un nucleo di C-O. In ambedue
i casi si perviene ad un'esplosione con energetica totale confrontabile con quella di una
supernova e in ambedue i casi l'intera struttura viene totalmente distrutta non sopravvivendo alcun residuo stellare compatto. Va ricordato che anche l'accrescimento di He
su una nana di He puo dare origine ad un innesco esplosivo con energetica comparabile
con quella di una supernova. Tuttavia, le caratteristiche di una tale esplosione non sembrano rispecchiare talune altre proprieta osservative tipiche delle SNIa ([?]). Va anche
ricordato che, invece, l'innesco degenere di H alla base di una shell relativamente sottile
di materia ricca di idrogeno intorno ad un nucleo di C-O da origine ad un evento esplosivo
dall'energetica tipica di una Nova.
66
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
2.8.1 Supernovae da Deagrazione del Carbonio
Si e visto in precedenza come al centro di una nana di C-O che approssima la massa
di Chandrasekhar si determinino le condizioni per un innesco degenere delle reazioni di
termofusione del carbonio. In natura questa condizione puo essere realizzata a seguito di
accrescimento diretto di C+O su una nana di C-O durante il processo di merging di due
nane di C-O prodotte in di due episodi di CE, ammesso che il tasso eettivo M_ CO con cui
procede l' accrescimento lo consenta. Anche in casi perticolari di accrescimento primario
di He o di H e possile, sebbene poco probabile, come si e visto, che il nucleo di C-O possa
raggiungere la massa di Chandrasekhar e subire un innesco centrale degenere delle reazioni
di termofusione del carbonio. Si conviene di denire l'inizio della fase di bruciamento del
carbonio quando l'energia persa dai neutrini eguaglia, in modulo, quella prodotta dalle
reazioni C12 + C12 (j" j = "CC ). In condizioni di forte degenerazione elettronica della
materia il processo di bruciamento termonucleare risulta reazionato positivamente. E
infatti inibita qualunque reazione strutturale di riaggiustamento volta al controllo della
temperatura (per esempio attraverso un'espansione) poiche l'equazione di stato assume
una forma del tipo P / indipendente da T.
Tuttavia, nonostante questa proprieta strutturale, i tempi che intercorrono tra il momento in cui j" j = "CC e quello in cui l'equilibrio idrostatico viene eettivamente rotto
non sono brevi (t 104 yrs). Durante questa fase evolutiva la temperatura centrale
continua a crescere a densita costante. Nel tentativo di rimuovere dalle zone centrali il
sempre crescente contributo energetico proveniente dalle reazioni di termofusione si instaura un trasporto convettivo la cui estensione aumenta in continuazione. La convezione
riesce eettivamente a rimuovere per lungo tempo l'energia prodotta per cui si registra
un netto aumento di luminosita superciale. Contrariamente a quello che si ritiene comunemente una supernova termonucleare, ad innesco centrale degenere del carbonio, non
compare improvvisamente in cielo sostituendo un oggetto precedentemente molto poco
luminoso e quindi non osservabile. Per tempi relativamenti lunghi, prima del breack-up
esplosivo, il progenitore deve essere osservabile come un oggetto blu compatto di alta
luminosita. L'energia prodotta dalle reazioni nucleari viene rimossa anche da un eÆcace usso neutrinico. In questa fase diviene particolarmente eÆciente la produzione
di neutrini URCA. All'interno del nucleo convettivo, attraverso i moti ascendenti e discendenti cui va soggetta la materia, si possono vericare reazioni simmetriche del tipo
(Z; A) + e ! (Z 1; A) + ! (Z; A) + e + . Le coppie piu signicative di nuclei
coinvolte in reazioni di questo tipo sono 21 F 21 Ne, 23 Ne 23 Na ed anche 25 Na 25 Mg
e 25 Ne 25 Na. L'unico eetto di queste reazioni e quello di sottrarre energia senza determinare mutamenti nelle specie nucleari presenti. In linea puramente ideale si puo supporre
che se esistessero in natura processi di perdita di energia particolarmente eÆcienti sarebbe
possibile evitare l'esplosione ed ottenere, come unico risultato, quello di trasformare la
2.8. Inneschi Termonucleari a Carattere Esplosivo
67
Fig. 2.12: Proli di temperatura all'interno di una struttura stellare di C-O in fase esplosiva distanziati
di 0.2 s l'uno dall'altro.
nana di C-O in un oggetto stellare con diversa composizione (Fe) ma dalla stessa natura
strutturale. Nei fatti, ad un certo istante evolutivo la temperatura centrale raggiunge un
valore per il quale la produzione di energia e cos elevata che la convezione ed i neutrini
non riescono piu a trasportarla. Da questo momento l'evoluzione procede su tempi scala
dinamici, dell'ordine dei secondi.
La gura 2.12, ([15]), mostra diversi proli di temperatura (in funzione della massa)
di una nana di C-O di 1.4 M in vari istanti durante l'evento esplosivo. Il primo (poco
distinguibile in gura a causa della sua vicinanza con l'asse delle ordinate) segue immediatamente l'istante in cui viene raggiunto il punto in cui l'energia non e piu rimovibile.
La temperatura sale immediatamente a circa 1010 K in una zona centrale di circa 0.01
M . Da un'analisi di g.2.13, ([15]), dove vengono riportati i proli di densita agli stessi
tempi di g. 2.12, si puo notare come a questo istante la densita non abbia ancora subito
radicali variazioni. La transizione di temperatura gia implica che nelle zone centrali si e
transitato da un profondo stato di degenerazione relativistica ad uno, sempre relativistico,
ma di degenerazione piu leggera. Gli strati centrali possono ora cominciare ad espandere
come deve fare un gas relativistico contenuto in un volume ristretto ad una temperatura
di 10 miliardi di gradi. Prima che l'espansione possa ridurre nuovamente la temperatura
e indurre una diminuizione della densita, le reazioni nucleari procedono a sintetizzare elementi sempre piu pesanti no al raggiungimento dell'equilibrio statistico nucleare (NSE)
con distribuzione degli elementi intorno al picco del ferro. Il bruciamento deve quindi
68
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.13: Proli di densita' all'interno della struttura di cui alla gura precedente agli stessi tempi
evolutivi.
propagarsi al resto della struttura. Si ritiene ragionevolmente che questo avvenga con
velocita di propagazione minori della velocita locale del suono (deagrazione).
Confrontando le gure 2.12 e 2.13 si puo osservare come man mano che il fronte di
combustione si propaga questo divenga sempre meno energetico e come la densita della
materia alle spalle del fronte divenga sempre piu bassa. Questo in virtu del fatto che
la materia interessata dal passaggio del fronte di combustione espande immediatamente
dopo il suo passaggio. In realta si puo notare dalla g. 2.13 che anche le parti di struttura
stellare antestanti il fronte espandono gia prima che questo le interessi direttamente, come
eetto indotto dall'espansione delle zone interne. Questa proprieta dipende dal fatto che
tutte le zone della struttura stellare sono in contatto sonico (il fronte si sposta infatti con
velocita sub-sonica) ed implica un crollo dell'eÆcienza del fronte (in termini di capacita di
indurre nucleosintesi e di cedere energia) dopo che questo ha attraversato soltanto poco piu
della meta circa della struttura stellare. Si comprende immediatamente che se la velocita
del fronte fosse stata supersonica (detonazione) gli eetti dell'esplosione sarebbero stati
nettamente piu rilevanti.
La gura 2.14, ([15]), fornisce la distribuizione degli elementi (in funzione della massa
interna della struttura) quando ormai l'eÆcienza delle reazioni di termofusine e divenuta
nulla e tutta la struttura sta denitivamente espandendo con un campo di velocita approssimativamente proporzionale al raggio. Si deve notare come esista una zona, dal
2.8. Inneschi Termonucleari a Carattere Esplosivo
69
Fig. 2.14: Distribuzione degli elementi sintetizzati durante un'esplosione centrale del carbonio.
centro no a circa Mr =M = 0:7, dove le reazioni nucleari sono state particolarmente
eÆcienti trasformando la materia originale in materia in NSE o prossima a questo. In
questa zona l'eÆcienza del fronte di combustione e stata totale. Successivamente a questa,
per un intervallo di massa di circa 0:2M , si nota una zona a composizione variabile. In
questa zona il fronte di combustione ha ridotto fortemente la propria intensita lasciando
alle sue spalle materia composta da specie sempre meno evolute nuclearmente (con la
notazione \Fe" in questa zona si intende 54 F e e 52 F e, mentre al centro si intende 56 F e).
Si nota inne la presenza di una zona esterna, di circa 0:5M , con composizione chimica
originaria. Qui non e avvenuta alcuna nucleosintesi apprezzabile. La composizione nale
della materia costituisce, quindi, una testimonianza dell'eÆcienza mantenuta dal fronte
combustione nell'attraversamento della struttura. Se il fronte si fosse mosso con velocita
supersonica piu di 1:3M di materia sarebbero state incinerate (trasformate in materia
in NSE).
In un evento esplosivo quale quello precedentemente descritto l'intera struttura viene
inne dissolta nello spazio circostante e, complessivamente, vengono liberati 1051 erg
distribuiti in massima parte in radiazione elettromagnetica ed energia cinetica del materiale espulso e, in parte nettamente minore, in neutrini. L'evento assume un aspetto
osservativo identicabile con una supernova di tipo Ia. La presenza dei nuclei di nichel
nelle zone centrali della struttura esplosa riveste un' importanza vitale per la formazione
della curva di luce. Infatti, il contenuto termico posseduto dalla struttura alla ne della
70
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
combustione impulsiva, viene presto assorbito dal processo di espansione. Se non esistessero altre fonti energetiche, la curva di luce prodotta dall'evento risulterebbe poco
luminosa e con sviluppo temporale limitato a tempi ridotti. Il nichel, invece, decadendo
secondo il processo 56 Ni ! 56 Co ! 56 F e con emissione di energia di 2.13 e 4.56 Mev
rispettivamente, e con tempi di dimezzamento rispettivamente di 6 e 77 giorni, non solo
contribuisce a determinare una curva di luce con massimo apprezzabilmente luminoso ma
contribuisce anche a determinare il tipico aspetto della parte discendente della curva di
luce a due pendenze con indice coincidente proprio con i tempi di dimezzamento dei due
decadimenti citati. La riproducibilita teorica delle curve di luce osservate delle SNe Ia ha
costituito un indubbio successo per il modello a deagrazione centrale del carbonio.
Una certa omogeneita, riscontrabile negli eventi di SN Ia, potrebbe trovare giusticazione nel fatto che eventi di deagrazione del carbonio, possibilmente all'origine di
almeno parte delle SN Ia osservate, sono eventi a soglia in cui questa e rappresentata
dal conseguimento della massa limite di Chandrasekhar da parte del nucleo stellare di
C-O. L'omogeneita o meno, degli eventi di SN Ia, e la possibile diversita dei progenitori,
costituiscono un problema attualmente aperto e di soluzione apparentemente non vicina.
Deve essere inne ribadito l'aspetto che le SN Ia sono dei produttori rilevanti di ferro
(piu di mezza massa solare per evento). Questo aspetto e confermato dalle osservazioni
(spettri e curve di luce) e vale aldila dei possibili dubbi che possano sussistere sulle proprieta e sull'unicita dei progenitori o dei meccanismi esplosivi.
2.9 Supernovae da Detonazione dell'Elio
Il capitolo si chiude descrivendo un altro evento esplosivo le cui caratteristiche possono
trovare riscontro osservativo in quelle delle SNe di tipo Ia. Se questo meccanismo sostituisce in natura quello descritto nel paragrafo precedente o se si aggiunge a quello, e ancora
materia di discussione.
Si e visto precedentemente come l'accrescimento di He su una nana di C-O possa
portare ad un innesco particolarmente violento delle reazioni 3 alla base dell'inviluppo
di He accresciuto. Perche il ash dell'elio risulti dinamico occorre che l'innesco avvenga
in presenza di degenerazione elettronica il che signica, restando la temperatura ssata
dalla necessita di innescare le reazioni nucleari, densita ragionevolmente elevata. Questa
proprieta si raggiunge quando si riesce ad accrescere una quantita apprezzabile di massa
prima che le reazioni 3 divengano pienamente eÆcienti (MHe > 0:2M ), in modo che
il ash possa avere origine in una regione della struttura ragionevolmente interna. Una
tale richiesta, come descritto precedentemente in questo stesso capitolo, si puo realizzare
quando in un sistema binario in fase evolutiva nale una stella di He trasferisce massa alla
compagna degenere di C-O (caso in cui M_ He assume valori consistenti con la formazione
di una detonazione dell'He nello strato accresciuto sulla nana di C-O) oppure, nel caso
2.9. Supernovae da Detonazione dell'Elio
71
di accrescimento di H, quando M_ H 10 8 M yr 1 e la massa iniziale della nana bianca
e circa 0:5 0:7M . Si notera come nel primo caso sia automaticamente soddisfatta
la condizione osservativa che indica l' assenza di idrogeno negli spettri delle SNe Ia.
Tuttavia, la presenza di un sottilissimo strato esterno di H propria del modello riportato
nel secondo caso, non implica l'esclusione di questo dalla rosa dei possibili progenitori
delle SNe Ia. E infatti ragionevole supporre che la quantita trascurabile di idrogeno
presente (MH < 10 4 M ) non sia suÆciente a far comparire questo elemento in modo
apprezzabile negli spettri (ammesso che non venga precedentemente bruciato dopo essere
stato inglobato nello strato convettivo di He che si forma subito dopo l'innesco in shell
delle reazioni 3).
La gura 2.15, [15], riporta diversi pannelli, a tempi successivi durante l'esplosione, in
cui vengono presentati, in funzione della massa interna del modello, gli andamenti di tre
variabili siche rilevanti: la temperatura (T9 , espressa in 109 K ), la densita (7 , espressa in
107 grcm 3 ) e la velocita (v9 , espressa in 109 cms 1 ). Si tratta di una nana di C-O di massa
originale di 0:6M accresciuta con He ad un tasso di M_ He = 10 6 M yr 1 che innesca
quando circa 0:3M di materia sono state accresciute su di essa. Si noti come la massa
totale al momento dell'innesco risulti nettamente inferiore alle 1:4M del modello descritto
nel paragrafo precedente. Questo aspetto giustica la denominazione sub-Chandrasekhar
attribuita a questa tipologia di esplosioni termonucleari degeneri. Come e consuetudine
viene assunto come zero il tempo in cui la convezione alla base dell'inviluppo di He non
e piu in grado di trasportare il surplus di energia generato dalle reazioni di termofusione
a fronte di una crescita non controllata della temperatura locale. Dopo 0.02 secondi
la temperatura raggiunge un picco locale di circa 3:5 109 K . Densita e velocita sono
ancora poco perturbate anche se e gia possibile individuare due zone, subito dentro e
subito fuori la shell di bruciamento dell'elio, dotate di campo di velocita rispettivamente
negativo (moto verso il centro) e positivo (moto verso la supercie). Dopo circa 0.2
secondi (pannello in alto a destra), il fronte di combustione ha gia raggiunto la supercie
ed e gia diminuito di intensita. Nello strato esterno di He si possono quindi ravvisare
modalita evolutive simili a quelle gia incontrate nel modello a deagrazione del carbonio
con la dierenza che qui il fronte di combustione ha origine in uno strato fuori centro e si
sposta a velocita supersonica (modello a detonazione fuori centro dell'elio). Il campo di
velocita nello strato esterno di elio appare nettamente denito ed orientato verso l'esterno
gia dopo 0.2 secondi. Ma l'aspetto piu importante, gia nettamente evidenziabile a questo
tempo, e la presenza di un'onda di compressione che dalla shell di elio si propaga verso
il centro. A t=0.29 s la presenza dell'onda diretta verso il centro e ancora piu evidente.
Finalmente, a t=0.628 secondi, l'onda raggiunge il centro dove si focalizza determinando
un aumento netto di temperatura e densita che producono un innesco indotto delle reazioni
di termofusione del carbonio in un ambiente degenere. Una situazione simile a quella che si
viene a creare al centro di un modello che innesca il carbonio alla massa di Chandrasekhar.
72
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
Fig. 2.15: Temperatura, densita e velocita della materia all'interno di una struttura che esplode per
innesco degenere fuori centro dell'elio a vari tempi durante l'esplosione. I tempi dei vari pannelli sono
espressi in secondi.
2.9. Supernovae da Detonazione dell'Elio
73
Fig. 2.16: Proli delle abbondanze degli elementi sintetizzati da un'esplosione sub-Chandraseckar
L'onda di termofusione si propaga subito verso l'esterno a velocita subsonica rimanendo
eÆciente no a quando raggiunge circa 0:5M . A t=1.397 secondi tutto e compiuto. Un
campo netto di velocita positive interessa tutta la struttura e diversi decimi di massa solare
di nichel sono pronti a decadere emettendo fotoni duri per alimentare la curva di luce.
La gura 2.16, [15], fornisce le abbondanze degli elementi sintetizzati durante il doppio
processo di combustione, detonatorio negli strati esterni e deagratorio in quelli interni.
Il prolo dell'abbondanza di Ni riette l'eÆcienza che i due fronti di combustione hanno
mantenuto durante la loro propagazione. Si puo notare una zona intermedia a composizione variabile dove si e spento il fronte interno ed una zona esterna di solo 0:1M
rimasta inalterata a causa dello spegnimento dell'onda di combustione esterna prima che
questa zona potesse essere raggiunta.
Il processo esplosivo determinato dall'innesco degenere fuori centro dell'elio non e
un meccanismo a soglia unica, come invece succede nel caso dell'innesco centrale del
carbonio. Si calcola che al variare di M_ He o di MW D;0 si produce una varieta di eventi con
energetica globale ed aspetto delle curve di luce diversi da caso a caso. Se questo aspetto
del modello ad innesco fuori centro degenere dell'He e compatibile con il complesso delle
evidenze osservative delle SNe Ia (o di parte di esse) deve essere ancora vericato.
Appendici
2.A Approfondimento A: La Geometria di Roche
Lo spazio di pertinenza di un sistema binario e sede di campi dovuti alle forze gravitazionali ed a quella
centrifuga. In un sistema di riferimento corotante con il sistema stellare, con origine coincidente la
componente piu massiccia del sistema, detta primaria, di massa M1, e con la secondaria (di massa M2)
giacente sull' asse x, come schematizzato in g. 2.17, il potenziale sara dato da
(x; y; z) = G Mr 1 + G Mr 2 + !2 [(x
1
2
2
M2
A)2 + y2 ]
M1 + M2
(2.18)
dove i termini entro la parentesi quadra corrispondono al quadrato del segmento d di g. 2.17 mentre
r12 = x2 + y2 + z 2, r22 = (A x)2 + y2 + z 2 e con la velocita angolare kepleriana di rivoluzione ! data
da !2 = G(M1 + M2)=A3
Nello studio di alcune proprieta dei sistemi binari (in particolare, per determinare il comportamento
cinematico della materia che uisce da una componente all' altra) si e trovato di grande utilita introdurre
un sistema di coordinate curvilinee ortogonali [1]. Nel 1969 Kopal [3] ha studiato in dettaglio le proprieta di queste coordinate decidendo di attribuire ad esse il nome di 'Coordinate di Roche' in onore del
matematico francese Edoardo Alberto Roche (1820-1883) che per primo aronto lo studio delle proprieta
cinematiche della materia in presenza di un dipolo gravitazionale rotante dotato di masse puntiformi.
La prima di queste coordinate, nella notazione di Kopal, assume una importanza particolare. Essa
fornisce la descrizione geometrica delle superci equipotenziali di valore assegnato. La geometria delle
superci equipotenziali, chiamata impropriamente geometria di Roche, presenta un aspetto complesso
ed inusuale. Una descrizione estensiva viene data da Kitamura [2], nel seguito ci si limitera a citare gli
aspetti piu rilevanti.
In prossimita di ciascuna delle due componenti stellari del sistema le superci equipotenziali assumono
forma di supercie sferica simile a quelle comunemente note in stelle singole. Ad una certa distanza si
incontra la prima superce singolare composta da due superci sferiche ablate, tangenti in un punto
singolare denito lagrangiano interno (L1). Tali \quasi sfere" tangenti in L1 vengono comunemente
denite lobi di Roche e ciascuna di esse contiene nel proprio centro una delle due componenti stellari
del sistema. L' intersezione con il piano dell'orbita di questa prima supercie singolare e facilmente
identicabile in g. 2.18 nella quale appare come un 8 rovesciato. Per un intervallo esteso di valori del
rapporto di massa q = M2=M1 il punto lagrangiano interno si trova in prossimita del centro geometrico
del sistema [4], e per questo motivo viene spesso identicato, ai ni pratici, con il punto in A/2. Per
distanze maggiori le superci equipotenziali assumono forma simile a superci ellissoidali e conuiscono,
74
2.A. Approfondimento A: La Geometria di Roche
75
Fig. 2.17: Forze gravitazionali e centrifuga agenti in un generico punto nello spazio di pertinenza di un
sistema binario con componenti di masse M1 ed M2 ruotanti intorno al centro di massa G con velocita
angolare !.
Fig. 2.18: Intersezione tra alcune superci equipotenziali di notevole interesse ed il piano dell'orbita in
un sistema binario con q=0.5. La primaria ha sede nell'origine e la secondaria sull'asse x a distanza
unitaria dall'origine. Sono indicati tre punti lagrangiani.
76
Capitolo 2. Sistemi Binari e Supernovae Termonucleari
successivamente, in due superci ellissoidali in cui uno degli apici costituisce un punto singolare denito
'lagrangiano esterno 2' e '3'. (In questi punti si realizza una tangenza tra la superce ellissoidale ed una
superce di forma circa cilindrica di estenzione indenita e perpendicolare al piano dell'orbita).
La gura 2.18 riporta, per semplicita, le intersezioni di alcune superci equipotenziali con il piano dell'
orbita avendo assunto per il rapporto di massa il valore q = 0:5. Una visione tridimensionale della
geometria di Roche, che a causa di una sua certa complessita risulta di lettura non immediata, si trova
in [2]. Si deve notare che quando q = 1 le superci singolari in (L2) ed in (L3) conuiscono in una sola
supercie con due singolarita simmetriche ai due apici opposti.
2.B Approfondimento B: Proprieta di Stelle con Inviluppi Convettivi
Si vuole mostrare come, in prima approssimazione, le dimensioni di una stella con profondi inviluppi
convettivi, sono poco dipendenti da variazioni di massa dell'inviluppo stesso. Fissando le idee su una
struttura stellare tipica di una gigante rossa con nucleo degenere ben sviluppato e ignorando la superadiabaticita superciale assumiamo un gradiente adiabatico per tutto l'inviluppo. Si avra quindi:
dlogT
r = dlogP
= cost
(2.19)
ad
ovvero:
P dT
T dP
= cost:
(2.20)
Si puo assumere, inoltre, che attraverso tutto l'inviluppo convettivo P = P (perche P 0), le
notazioni b ed s essendo riferite, rispettivamente, alla base dell'inviluppo convettivo ed alla sua superce
che coincide, in pratica, con la superce della stella. Attraverso una sostituzione nella 2.20 si ottiene
che T = (T T ) = cost T . Siccome T dipende solo dalle proprieta del nucleo stellare degenere,
risulta che la variazione di temperatura attraverso l'inviluppo convettivo non e funzione della massa
dell'inviluppo stesso. Nell'inviluppo convettivo non ci sono sorgenti di energia, per cui si ha che L =
L = 4R2 T 4. Anche L dipende solo dalla massa del nucleo, pertanto si ottiene che, ad una prima
cruda approssimazione, il raggio di una struttura in fase di gigante rossa (o di ramo asintotico) non
dipende dalla massa dell'inviluppo stesso. Il calcolo dettagliato dei modelli oltre a mostrare che in
realta il raggio aumenta al diminuire della massa dell'inviluppo, mostra anche che questa proprieta e
vericata no a quando la massa dell' inviluppo non scende sotto una massa critica dell' ordine di pochi
decimi di massa solare, e il cui valore preciso dipende solo dalla luminosita [5]. Per valori della massa di
inviluppo inferiori a tale valore critico l'evoluzione della stella e denitivamente segnata: veloce escursione
verso valori sempre minori del raggio (alte temperature eettive) a luminosita circa costante e, inne,
rareddamento continuo, a raggio costante, lungo la sequenza delle nane bianche.
b
b
s
b
s
b
b
s
e
b
2.C Approfondimento C: Eetti del Common Envelope sulla
Separazione
Durante l'evoluzione di Common Envelope la separazione di un sistema binario tende a diminuire non
fosse altro per il fatto che le due componenti orbitano in un mezzo a densita non nulla con eetti di
attrito non trascurabili. Tuttavia, la determinazione precisa della nuova separazione del sistema a evento
2.C. Approfondimento C: Eetti del Common Envelope sulla Separazione
77
di Common Envelope concluso costituisce un problema di soluzione non facile che richiede una trattazione
idrodinamica dettagliata non ancora disponibile. Iben e Tutukov, [6], hanno proposto di stimare la nuova
separazione A0 , a partire dalla vecchia, A, utilizzando la seguente relazione che successivamente e stata
largamente utilizzata da diversi autori:
M M
A0 = 1 2 2 A
M1
(2.21)
dove M1; M1 ed M2 sono rispettivamente la massa originale della primaria, quella del suo resto alla ne
del CE e la massa della secondaria che si assume invariata a seguito all'episodio di CE. Il parametro e
un parametro libero adimensionale dell'ordine dell'unita
La relazione di Iben e Tutukov deriva, attraverso un certo numero di approssimazioni, dalla seguente
identita:
;r
;r
GM1 M2
A0
1
= GM
(2.22)
A
dove il primo membro e una misura della decrescita dell'energia di legame del sistema (E = GM1M2=2A)
avendo assunto A0 < A, mentre il secondo membro rappresenta l'energia necessaria per portare all'innito,
a velocita zero, l'inviluppo della primaria (M1 M1 ), assumendo (M1 M1 ) M1 dato che M1 M1 .
Il parametro e quindi una misura di quanta energia orbitale sia stata eettivamente utilizzata per
espellere l'inviluppo della primaria. L'approsimazione di Iben e Tutukov, che ha trovato un vasto impiego
operativo, puo essere riformulata, evitando approssimazioni, nel modo seguente:
2
;r
L
;r
A0 = ;r
M1
;r
(2.23)
2M1 M1 A
Si deve far notare come l' utilizzo della 2.23, in sostituzione della 2.21, anche se formalmente piu corretto,
non dia alcuna garanzia sulla validita del risultato. I risultati forniti da queste relazioni vanno considerati
con estrema cautela ricordando sempre che l'assunzione che ha consentito di derivarle potrebbe vericarsi
inadeguata aldila di una ragionevole variaziane del parametro .
;r
;r
Bibliograa
[1] Prendergast, K.H., 1960, Ap. J., 138, 162
[2] Kitamura, M.,1970 Astrophys. Space Sci., 7,272
[3] Kopal, Z., 1969, Astrophys. Space Sci., 5,360
[4] Cox & July
[5] Castellani, M., & Tornambe, A., 1991, Ap. J., 381, 393
[6] Iben, I., Jr., & Tutukov, A., 1984, Ap. J., 282, 615
[7] Landau, L. & Lifshitz, E., 1966 Theorie du Champ, Tome II, MIR
[8] Nomoto, K., & Iben, I., Jr., 1985, Ap. J., 297,531
[9] Fujimoto, M.,Y., & Sugimoto, D., 1982,Ap. J.,257, 291
[10] Bravo, E., Tornambe, A., Dominguez, I., & Isern, J., 1996, A&A, 306,822
[11] Whelan, J.C. & Iben, I.Jr., 1973, Ap. J., 186, 1007
[12] Cassisi, S., Iben, I.Jr. & Tornambe, A., 1998, Ap. J., 496, 376
[13] Piersanti, L., Cassisi S., Iben, I.Jr. & Tornambe, A., 1999, Future directions of Supernovae Research: progenitors to remnants, Mem. S.A.It., Cassisi, S., Mazzali P.
Eds.
[14] Limongi, M. & Tornambe, A., 1991, Ap. J., 371, 317
[15] Cortesia di Eduardo Bravo
[16] Risultati inediti del gruppo di Evoluzione Stellare dell'Osservatorio Astronomico di
Collurania - Teramo
78