Aspetti generali della Fisica Atomica e della Fisica Nucleare collegati ai metodi di datazione e
alle analisi non distruttive.
Premessa.
La maggior parte dei metodi di datazione utilizzati nell'Archeologia e nella Storia dell’Arte,
principalmente il metodo del C14, che é direttamente basato sulla legge di decadimento della
radioattività di questo isotopo, e il metodo di datazione della termoluminescenza (TL), che si basa
sulla dose di radiazioni dovuta ai radioisotopi naturali (U235,U238,Th232,K40) assorbita dal campione
in esame, fanno ricorso al fenomeno della radioattività. Inoltre, per comprendere appieno il
significato dell’attributo non distruttivo assegnato ai metodi atomici o nucleari impiegati per
l’analisi dei Beni Culturali é necessario avere chiari, più in generale, alcuni elementi di base della
Fisica Atomica della Fisica Nucleare.
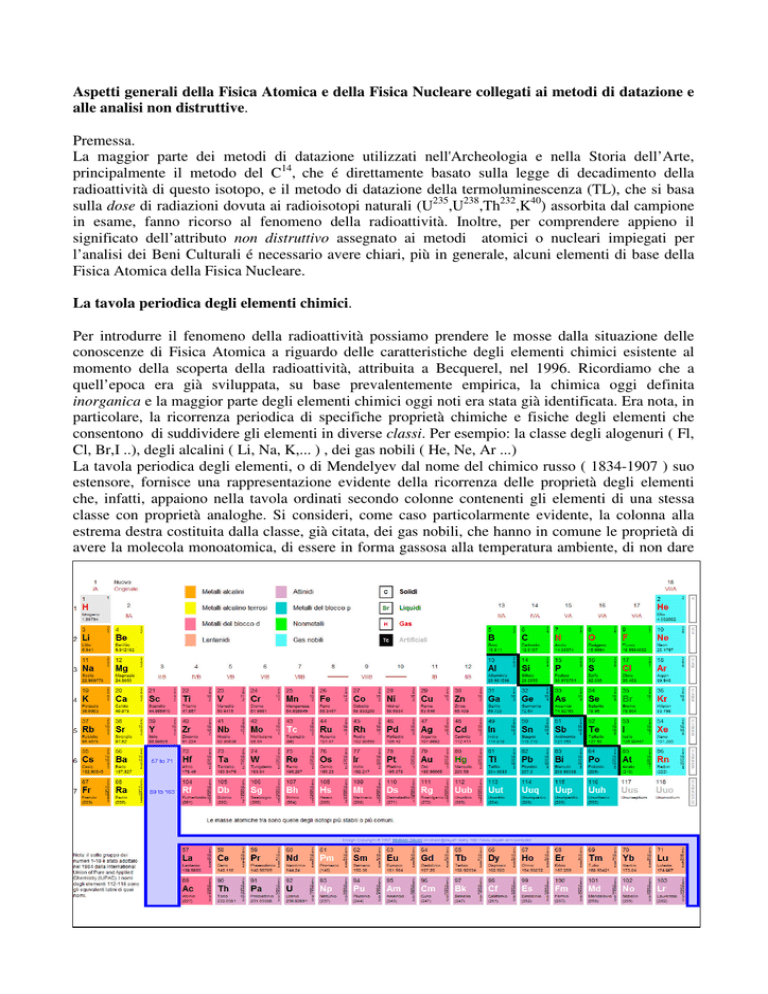
La tavola periodica degli elementi chimici.
Per introdurre il fenomeno della radioattività possiamo prendere le mosse dalla situazione delle
conoscenze di Fisica Atomica a riguardo delle caratteristiche degli elementi chimici esistente al
momento della scoperta della radioattività, attribuita a Becquerel, nel 1996. Ricordiamo che a
quell’epoca era già sviluppata, su base prevalentemente empirica, la chimica oggi definita
inorganica e la maggior parte degli elementi chimici oggi noti era stata già identificata. Era nota, in
particolare, la ricorrenza periodica di specifiche proprietà chimiche e fisiche degli elementi che
consentono di suddividere gli elementi in diverse classi. Per esempio: la classe degli alogenuri ( Fl,
Cl, Br,I ..), degli alcalini ( Li, Na, K,... ) , dei gas nobili ( He, Ne, Ar ...)
La tavola periodica degli elementi, o di Mendelyev dal nome del chimico russo ( 1834-1907 ) suo
estensore, fornisce una rappresentazione evidente della ricorrenza delle proprietà degli elementi
che, infatti, appaiono nella tavola ordinati secondo colonne contenenti gli elementi di una stessa
classe con proprietà analoghe. Si consideri, come caso particolarmente evidente, la colonna alla
estrema destra costituita dalla classe, già citata, dei gas nobili, che hanno in comune le proprietà di
avere la molecola monoatomica, di essere in forma gassosa alla temperatura ambiente, di non dare
luogo ad alcun composto con altri elementi. Un altro caso evidente é rappresentato dalla classe degli
alogenuri, nella quale uno degli elementi, ad essa appartenente, può combinarsi con uno degli
elementi alcalini per formare i più comuni sali, come il cloruro di sodio, o sale da tavola, ( NaCl )o
con uno degli alcalini terrosi per formare, per esempio,il fluoruro di calcio ( CaFl ). Ancora a
proposito della classe dei gas nobili, si noti che l’atomo di elio (He ), che, in base alla attuali
conoscenze, sappiamo che ha numero atomico, Z, = 2 e, quindi, é attiguo a l’idrogeno (H) che ha
Z= 1, non si trova accanto all’idrogeno ma, sorprendentemente, alla estrema destra nella prima riga
della tavola nel primo posto in alto nella colonna dei gas nobili.
La grande intelligenza e perspicacia di Mendelyev é stata di avere trovato la collocazione corretta di
tutti gli elementi noti al suo tempo e di avere addirittura previsto che dovessero esistere caselle della
tabella, allora ancora vuote, per elementi che furono, in effetti, scoperti in seguito come, per
esempio, il germanio (Ge). Ciò solamente sulla base della osservazione empirica della ricorrenza
delle proprietà chimiche e fisiche dei diversi elementi.
Al giorno d’oggi, basandoci sui risultati della meccanica quantistica, di molti anni posteriore alla
tavola di Mendeleyev, é semplice interpretare la periodicità delle proprietà atomiche in base alla
descrizione della sequenza degli orbitali (o stati) atomici occupati dagli elettroni che sono contenuti
in un atomo di numero atomico via, via crescente. (Ricordiamo che il numero di elettroni – di carica
negativa - é esattamente lo stesso di quello dei protoni – che hanno carica positiva –: cioé, Z e la
carica del protone e dell’elettrone é la stessa in valore assoluto cosiché l’atomo é neutro
elettricamente).
La meccanica quantistica prevede, in contrapposizione con la meccanica classica:
a) che i diversi orbitali stabili per i Z elettroni dell’atomo sono ordinati in una sequenza definita,
b) che ciascun orbitale contiene un determinato numero massimo di elettroni,
c) che ciascuno orbitale ha una caratteristica energia di legame.
E’ dovuto a queste regole quantistiche per il riempimento progressivo da parte degli elettroni di
questa serie discreta di stati legati dell’atomo fino a raggiungere il numero Z che si determina
corrispondentemente l’energia di legame di ciascuno stato e, inoltre, che si giustificano, in base alla
sequenza degli stati elettronici esterni.le leggi di ricorrenza di alcune proprietà chimiche e fisiche
delle diverse classi atomiche.
La sequenza degli orbitali stabili, può essere ottenuta a partire da quella dalle shell elettroniche (in
Inglese shell=guscio), o livelli nella quale sono preliminarmente ripartiti gli elettroni atomici
secondo i possibili valori di energia di legame. Le shelles sono contrassegnate con le lettere K, L,
M.,N,O a partire dalla più interna verso l’esterno. A ognuna di esse è associato il numero quantico
principale, n, che varia da 1 a 5.. Nel caso dell’atomo di Idrogeno, esiste un solo elettrone nella
shell K. L’orbitale è di tipo S e denominato: 1S l’energia di legame dello stato 1S è di circa 13
elettron Volt. L’atomo di elio contiene 2 elettroni. Perciò esso contiene un secondo elettrone nello
stato 1S. Il numero massimo di elettroni di uno stato S, indipendentemente da quale sia la shell alla
quale appartiene è 2. Ciò comporta che, passando al Litio (Z=3), l’aggiunta di un terzo elettrone,
corrisponde al formarsi del secondo livello (L shell) con numero quantico principale n=2. Lo stato
quantico del primo elettrone nella shell L é ancora di tipo S ed é chiamato 2S. Se si aggiunge un
ulteriore elettrone per formare il boro (Z=4), lo stato 2S é, a sua volta, completo e i seguenti
elettroni degli atomi via,via più pesanti vanno a occupare il secondo stato, denominato 2P, previsto
per il livello L. Ciascuno stato P si completa con 6 elettroni (Si noti che non esiste lo stato 1P nella
shell K, ma il primo stato P appare nella shell L ). Dopo avere aggiunto la condizione di chiusura
con 6 elettroni, abbiamo un totale di 10 elettroni in corrispondenza. per Z= 10, del gas nobile Neon.
Ricordiamo che Elio e Neon , entrambi gas nobili, hanno proprietà analoghe. Ciò corrisponde con il
fatto che in entrambi i casi l’orbitabile più esterno (che é lo stato 2S nel caso dell’Elio) é chiuso. In
questa condizione l’atomo non possiede elettrone esterni che rendano possibile il formarsi di un
legame con un altro atomo e ciò spiega qualitativamente le caratteristiche già citate dei gas nobili.
In generale, le caratteristiche di un atomo, dipendono dalle proprietà dello stato elettronico più
esterno. I casi più evidenti, oltre a quello che lo stato sia chiuso, sono che all’atomo manchi solo un
elettrone per aversi la chiusura dello stato esterno (caso degli alogenuri) o, invece, esso abbia un
elettrone in esubero subito dopo la chiusura dello stato dell’atomo precedente, cioé con numero
atomico pari a Z-1 (caso degli alcalini). Allora, il formarsi dei sali per combinazione alcalinoalogenuro, già menzionato, si spiega qualitativamente, immaginando che l’elettrone dell’atomo
alcalino sia un gancio sporgente che si aggancia all’asola costituita dal posto vuoto nell’orbitale
dell’alogenuro.
Come già detto, a ciascuno degli orbitali elettronici dell’atomo é associato un valore, caratteristico
di energia di legame per l’elettrone che dipende in modo più che proporzionale da Z e ha il valore
massimo per lo stato più interno, 1S , e decresce progressivamente spostandosi sugli stati via,via
più esterni.
Iniziamo con il notare, allora, che occorre irraggiare un atomo, per esempio con radiazione
elettromagnetica, di energia fortemente crescente con il valore del numero atomico Z per provocare
l’espulsione di un elettrone (fenomeno della ionizzazione). In uno stesso atomo, questa energia é
molto maggiore per la shell K e ,immediatamente a seguire, per la shell L, di quella necessaria per
ionizzare uno stato elettronico esterno. La shell K, e poi la shell L, hanno dunque la massima
energia di legame.
Corrispondentemente, quando un elettrone di uno stato esterno cade nella vacanza lasciata libera
nella shell K per effetto della ionizzazione, l’energia della radiazione X emessa dall’atomo é
massima. Se l’elettrone proviene da uno degli stati 2P della shell L ( una regola di selezione della
meccanica quantistica proibisce la transizione 2S – 1S ), si ha l’emissione di una delle righe di
fluorescenza X caratteristica, Kα1 o Κα2, a seconda dello stato di partenza. Se l’elettrone che
rimpiazza l’elettrone mancante alla shell K proviene da uno degli stati della shell M, si ha una delle
righe X della serie Kβ che hanno energia maggiore. In generale, l’energia della radiazione X
emessa è pari alla differenza delle energie di legame fra stato elettronico interno di arrivo e stato
esterno di partenza. Quindi, l’energia delle righe Kβ è maggiore poiché l’energia di legame degli
stati della shell, di partenza, M è minore di quella degli stati della shell L.
L’analisi della composizione di un dato campione basata sulla misura della energia delle righe X
dovute a transizioni agli stati elettronici delle shell K e L é denominata analisi XRF (X-ray
fluorescence = fluorescenza X.).
L’energia della radiazione di fluorescenza X aumenta più che linearmente con il valore di Z
dell’atomo emettitore. Per esempio la riga Kα1 ha un’energia di 7.5 Kev per il rame (Z= 29), di 22
Kev per l’argento (Z= 47 ), di 75 Kev per il piombo (Z=82). Lo spettro di emissione X prodotto dai
diversi elementi chimici nel campione in analisi é detto a righe (o a linee) poiché le energie dei
raggi X caratteristici emessi dagli atomi hanno un valore determinato con estrema precisione (o
definizione) corrispondente alla differenza delle energie di legame fra 2 stati atomici. I valori
dell’energia delle righe Kα e Kβ e delle righe L caratteristici dei singoli atomi, sono stati misurati
per tutti gli atomi. Ciò consente di individuare qualitativamente la composizione elementare (da
elemento chimico) del campione in analisi, in pratica, senza ambiguità. Infatti, non esistono
sovrapposizioni dei valori di energia fra le righe Kα di due atomi diversi. Si verificano, invece,
alcuni casi di sovrapposizione per l’energia di una delle righe L emessa da un elemento pesante e
l’energia di una riga Kα ο Κβ emessa da un elemento leggero, ma le informazioni aggiuntive che si
hanno sulla natura del campione permettono di solito di identificare di quali elementi si tratti.
Se, in generale, i fenomeni di transizione elettronica riguardano gli stati elettronici esterni che ,
come già notato, hanno bassi valori di energia di legame, essi sono caratterizzati da assorbimento e
emissione di radiazione a bassa energia. Questo é il caso del metodo di analisi, largamente utilizzato
nei laboratori, denominato di spettroscopia atomica ottica, che può essere di emissione o di
assorbimento a seconda che l’analisi sia basata sulla misura delle energie (o delle lunghezze
d’onda) della radiazione emessa dagli atomi o della radiazione assorbita. La radiazione
elettromagnetica dello spettro visibile o della zone immediatamente vicine ha energia dell’ordine
dell’elettron-volt.. La spettroscopia ottica rappresenta un metodo di analisi distruttiva poiché si
richiede il prelievo di un piccolo campione dall’oggetto in analisi., eventualmente la sua diluizione
o un opportuno trattamento chimico e, di solito, la sua evaporazione.
Precisazioni sul significato dell’attributo non distruttiva assegnato alla analisi XRF.
Si consideri anzi tutto che non distruttiva nel caso delle analisi di Beni Culturali deve essere inteso
in una accezione fortemente restrittiva. Cioè: che l’analisi non arrechi alcun tipo di
danneggiamento. Un danneggiamento del campione dovuto al metodo di analisi deve essere inteso
come una possibile modifica della composizione chimica e dipende dal fatto che nell’analisi siano
coinvolti gli stati elettronici più esterni dell’atomo che, infatti, sono quelli che partecipano alla
formazione del legame chimico fra diversi atomi. Questo effetto é escluso quando l’analisi è
eseguita con radiazione di energia sufficientemente alta perché sia possibile ionizzare gli stati
elettronici interni dell’atomo che non hanno alcun ruolo nel formare il legame chimico. Da ciò
traiamo la fondamentale giustificazione per il fatto che l’analisi XRF é non distruttiva .Inoltre,
questo argomento è valido, a maggior ragione, se l’analisi è basata su reazioni nucleari poiché non
vi è alcuna correlazione fra i livelli energetici del nucleo è gli orbitali elettronici.
Il motivo ulteriore per il quale le analisi XRF e quelle nucleari sono da considerarsi non distruttive
(o non invasive ) è che il segnale elettrico prodotto nel rivelatore dal quanto di radiazione di elevata
energia emesso da un singolo atomo, o nucleo, possiede un’ampiezza sufficiente perché si abbia un
segnale effettivamente rivelabile. Ciò corrisponde a eseguire una misura,“un atomo per volta”,su un
numero di atomi sufficientemente grande per raggiungere una adeguata consistenza statistica.
Considerando il numero grandissimo di atomi presenti in un campione, anche se microscopico, il
numero di atomi ionizzati nell’analisi costituisce una minima percentuale.Ma è importante notare
che questo numero è statisticamente significativo anche se si adoperano valori di intensità per la
radiazione incidente di alta energia così bassi da rendere trascurabili gli effetti, in linea di principio
dannosi, dovuti agli effetti di ionizzazione degli orbitali a bassa energia di legame prodotta nella
stessa analisi,.
Nel caso della spettroscopia ottica, già citata, l’intensità luminosa dovuta alla emissione di un
singolo atomo è troppo flebile e, quindi, é necessario misurare le emissioni emesse
contemporaneamente da un gran numero di atomi del campione. Ciò è ottenibile utilizzando elevate
intensità per la radiazione incidente e lavorando su un campione precedentemente vaporizzato per
minimizzare gli effetti di auto-assorbimento che impediscono alla radiazione luminosa di propagarsi
in un mezzo denso.
A proposito dell’auto-assorbimento, si consideri che le radiazioni X possono penetrare in profondità
nel campione in analisi, ( per un metallo lo spessore analizzabile vale circa 10 micron come valore
medio). A loro volta, le radiazioni X emesse, di alta energia, possono fuoriuscire dal campione da
uno spessore dello stesso ordine senza che sia necessaria alcuna preparazione del campione stesso.
Si noti, infine che,in generale, le analisi XRF sono eseguibili in loco con apparecchiatura portatile.
Nozioni generali sulla radioattività
L’anno della scoperta della radioattività (1896) può a buona ragione essere considerato quello della
nascita della Fisica Nucleare. Senza dubbio si é trattato, infatti, della prima evidenza sperimentale
di un fenomeno nucleare, identificato negli anni seguenti come dovuto al decadimento dei nuclei
atomici instabili. Più correttamente, l’anno di nascita della Fisica Nucleare dovrebbe essere
considerato il 1911, anno nel quale Rutherford eseguì l’esperienza cruciale che ha provato
l’esistenza del nucleo atomico. Come é ben noto, l’esperienza di Rutherford consistette nella misura
sperimentale del fenomeno della deviazione subita nell’attraversare un sottile foglio d’oro dalle
particelle α emesse dal Radio 226 (isolato dal minerale uranifero da madame Curie) . La grandezza
osservata sperimentalmente della deviazione della traiettoria di questi proiettili si spiega solo con
l’ipotesi che al centro dell’atomo esista un nucleo positivo, di dimensioni trascurabili rispetto al
volume atomico, che racchiude l’intera carica positiva, che oggi sappiamo essere quella costituita
da Z protoni. L’atomo é circondato dalla nube di Z elettroni, a distanza grandissima rispetto il
raggio del nucleo. L’atomo ha carica totale nulla, ma la disposizione delle cariche corrispondente
alla configurazione di un volume puntiforme positivo fortemente repulsivo per le particelle α, anche
esse positive, spiega correttamente la deviazione da esse subita. Si noti che l’altro modello
alternativo dell’atomo, proposto da Thomson, era basato su una distribuzione di cariche positive e
negative uniformemente mescolata all’interno del volume dell’atomo. Questo modello non sarebbe
compatibile con il fenomeno della deviazione delle α misurato da Rutherford.
Anche per illustrare le nozioni generali riferite alla radioattività, possiamo prendere le mosse dalla
tabella di Mendeleyev e ricercare in essa la posizione occupata dagli atomi radioattivi naturali.
Notiamo subito, però,che per ottenere la trasformazione da questa nella attuale tabella dei nuclei
che contiene gli atomi stabili e quelli instabili- cioè, quelli radioattivi naturali e artificiali- dovremo
introdurre la nozione di isotopo. Gli isotopi furono scoperti nel 1934 da Soddy e, forse,
definitivamente questa potrebbe essere considerata la data di nascita della Fisica Nucleare,nel senso
che la scoperta degli isotopi ha reso possibile la sistemazione nella nuova tavola di tutti i nuclei
esistenti (non più detta degli elementi) molto più numerosi degli atomi conosciuti al tempo di
Mendeleyev.
Partiamo dalla osservazione della tavola degli elementi, esistente nel 1896, per ricercare che
posizione vi occupano gli atomi radioattivi naturali, includendo fra essi quelli identificati negli anni
seguenti la scoperta della radioattività, ma prima della scoperta fondamentale del neutrone, che ha
reso possibile la produzione dei nuclei radioattivi artificiali.
La ricerca dà come risultato che non esistono in natura elementi stabili con numero atomico Z
maggiore di 83, corrispondente al bismuto (Bi).L’unica eccezione di elemento naturale instabile con
numero atomico minore di 83 é il tecnezio ( Z = 43).
Per gli elementi naturali il valore massimo di Z é 92 (Uranio: U), per Z maggiore di 83, si hanno
solo elementi radioattivi. Ricordiamo che la radioattività coincide con il fenomeno della instabilità
nucleare cioé con il fenomeno per cui alcuni atomi, per il momento limitandoci a quelli naturali,
sono instabili e tendono a trasformarsi ,o a decadere, in un atomo con il nucleo stabile, dando luogo
a un processo di decadimento nel quale ,a seconda dei casi, si ha l’emissione di un particella α, di
un elettrone positivo, di un elettrone negativo, (decadimenti β ) o, infine, caso meno noto, nel
processo di decadimento nel quale si ha la cattura di un elettrone dell’atomo stesso ( e.c. = electron
capture). Tutti i processi di decadimento hanno in comune che lo stato finale – nucleo residuo +
particella emessa- ha massa totale inferiore a quella del nucleo instabile emettitore. Questa
condizione é necessaria ma non sufficiente per dar luogo a un nucleo radioattivo e porta
immediatamente a ricavare l’energia che si libera nel decadimento dalla formula famosa E = ∆mc2
nella quale la variazione ∆m rappresenta la differenza fra massa iniziale del nucleo e somma delle
masse del sistema finale. Si noti che nella maggior parte dei casi il nucleo residuo prodotto dal
decadimento ( nucleo finale )si forma in uno stato eccitato e che la diseccitazione avviene mediante
emissione di raggi γ con ulteriore diminuzione della massa del nucleo finale.
Il fenomeno della instabilità nucleare si spiega facendo ricorso alla descrizione della struttura del
nucleo, così come determinata dopo la scoperta del neutrone.
Un nucleo é composto da Z protoni e N neutroni. Le proprietà chimiche dell’atomo dipendono solo
da Z al quale corrisponde il simbolo chimico ( H, He, Li, ecc. ) in corrispondenza dei diversi numeri
N per ciascun elemento con lo stesso Z si hanno gli isotopi . Il nome deriva dal Greco (stesso posto
) e fa riferimento al fatto che tutti gli isotopi con lo stesso Z figurerebbero nella stessa posizione
nella tavola di Mendeleyev in quanto hanno le stesse proprietà chimiche. Il simbolo dell’isotopo è
quello chimico, che corrisponde al valore di Z dell’elemento, associato al numero di massa A, Per
es,: C14, Pb 208, U235.
L’esistenza dei neutroni nel nucleo si spiega qualitativamente con l’attribuire a essi la funzione di
tenere insieme il nucleo controbilanciando la repulsione elettrica esercitata reciprocamente dai
protoni. L’effetto totale di tale repulsione, che é la causa della instabilità, aumenta come Z2 , la
conseguenza é che il numero di neutroni per ottenere un nucleo stabile aumenta progressivamente
con Z in maniera più che proporzionale. Per gli elementi leggeri , cioé per Z ≤∼20, gli isotopi stabili
hanno un valore di N praticamente eguale a Z; poi il numero di neutroni in eccesso diviene sempre
maggiore. Per l’elemento stabile più pesante esistente in natura, il bismuto, si ha: Z = 83, N= 126
(!). Se Z aumenta oltre 83, non esiste più la possibilità di ottenere un nucleo stabile , cioé non si
realizza la possibilità che l’attrazione dovuta alle forze nucleari fra i nucleoni, aumentata
dall’eccesso di neutroni, compensi stabilmente la repulsione Coulombiana dovuta ai protoni.
L’ elemento con Z = 92 (Uranio) ha due isotopi con tempo di dimezzamento confrontabile con l’età
della terra. Essi sono U235 che ha N= 143 e U 238 ,che ha N=146. Inoltre, l’elemento con Z=90
(Torio) ha l’isotopo,con N= 142 (Th232 ), con un tempo di dimezzamento dell’ordine di 10 10 anni.
Th232 , U235 e U238 sono gli isotopi capostipite delle serie radioattive naturali 4n, 4n+3, 4n+2 . Tutti
gli isotopi radioattivi naturali fanno parte di una delle 3 serie che terminano, rispettivamente, con gli
isotopi stabili Pb 208, Pb207,Pb206 . L’unico isotopo radioattivo naturale che non appartiene a una
delle serie radioattive ed é presente in natura perché ha un tempo di dimezzamento maggiore di 109
anni é il K40.
Avendo introdotto nella descrizione degli atomi gli isotopi, possiamo descrivere la tavola dei nuclei
che sostituisce quella di Mendeleyev nella quale non esistono gli isotopi.
In questa carta per ciascun valore di Z, riportato sulla coordinata Y, figurano gli isotopi in
corrispondenza dei diversi valori di N, riportati sulla coordinata X. Gli isotopi stabili per gli
elementi leggeri hanno valore di N prossimo a quello di Z, mentre per gli elementi
progressivamente più pesanti ,come già detto, il valore di N degli isotopi stabili aumenta rispetto a
quello di Z, Quindi se rappresentiamo nel piano N-Z i punti rappresentativi degli elementi stabili
naturali otteniamo che essi si dispongono su una curva che ha un andamento secondo la diagonale (
cioé, con Z=N) all’inizio, per seguire una curva progressivamente più bassa (cioè: con N>Z ) fino i
punti finali rappresentativi degli isotopi stabili del piombo.
Possiamo aggiungere agli isotopi naturali stabili e a quelli, poco numerosi, instabili la grande
quantità di isotopi instabili artificiali che si generano nelle reazioni nucleari artificiali ottenute con
acceleratori di ioni o con reattori nucleari che producono neutroni.Gli isotopi instabili si allineano in
alla quota determinata del valore di Z dell’elemento: a sinistra del valore, o dei valori, di N che
corrispondono a nuclei stabili; gli isotopi caratterizzati da un difetto di neutroni. a destra quelli
caratterizzati da un eccesso di neutroni. I primi decadono con emissione β + nella quale un protone
si trasforma in un neutrone o, molto più frequentemente, si ha il fenomeno della cattura elettronica
nel quale avviene la stessa trasformazione. Gli isotopi di destra, cioè con eccesso di neutroni, danno
luogo al decadimento β − nel quale un neutrone si trasforma in un protone. Si noti che in entrambi i
casi, il decadimento avviene fra due isotopi isobari, cioè con lo stesso numero di massa A. Infatti in
un decadimento β il numero di nuleoni- protoni+neutroni – resta invariato. Il decadimento α,
invece, dà luogo a una diminuzione di Z pari a 2 e di A pari a 4.
Il numero di isotopi artificiali prodotti negli ultimi 50 anni raggiunge quasi 3000 (!) cioé supera di
gran lunga quello dei naturali stabili e instabili.
Notiamo, infine, che due isotopi dello stesso elemento hanno delle piccole differenze nell’emissione
ottica dei quali non trattiamo. Inoltre, l’equivalenza di comportamento chimico per due diversi
isotopi é verificata a meno di effetti del secondo ordine che non sempre sono trascurabili. Per
esempio, nel processo di sintesi clorofiliana nel quale si formano i vegetali utilizzando la CO2
dell’atmosfera si ha una riduzione percentuale di C13 e C14 e questo fenomeno non può essere
trascurato senza commettere un grande errore nel metodo di datazione con C14
Elementi di Statistica
Vogliamo in ultimo occuparci dell’aspetto molto importante delle misure di conteggio: cioè
dell’errore statistico che é contenuto inevitabilmente nel risultato che con un opportuno contatore si
ottiene per la misura del numero di radiazioni emesse da un isotopo radioattivo in un determinato
intervallo di tempo. Notiamo immediatamente che qualsiasi misura sperimentale contiene sempre
un errore e che, in genere, il valore dell’errore dipende sia dalla imprecisione dello strumento di
misura o del metodo di misura, sia dal fatto che la quantità che misuriamo ha una sua intrinseca
dispersione di valori (Immaginiamo, per esempio, di misurare l’altezza di un gran numero di
individui. La dispersione dei valori misurati dipende certamente dalla variazione dell’altezza nella
popolazione e, di solito secondariamente in questo caso, dalla possibile imprecisione del metodo di
misura).
Per renderci conto di come si tratti il problema dell’errore in una misura di conteggio, prendiamo
per confronto una misura che si riferisca al numero, n, di monete che danno testa nel lancio di 100
monete sul tavolo. La stretta analogia fra decadimento nucleare e lancio delle monete risiede nel
fatta che in entrambi i casi abbiamo una situazione che si definisce binaria per gli eventi in misura:
cioèsi ha, rispettivamente, che un atomo decade o non decade nel tempo di misura e che il lancio di
una moneta dà testa o croce. E la misura consiste semplicemente nel misurare il numero di eventi.
Sappiamo che ogni volta sarà approssimativamente n=50, se ripetiamo,infatti, il lancio un numero
elevato di volte, ci aspettiamo che il suo valore medio in effetti sia molto prossimo a 50. Ma ci è
evidente che la variazione nel numero di teste, ottenuto in ogni lancio non dipende da un errore nel
modo di eseguire il lancio, ma é intrinsecamente dipendente dal fatto che l’evento (testa) ha di
ripetibile in ogni lancio la probabilità di verificarsi che, ovviamente se le monete non sono truccate,
é costante e del 50 % . Si può dimostrare che, indicando con m il valore medio di n, per il valore
medio della differenza, n–m, (che in seguito chiameremo deviazione standard, σ ) teoricamente si
ha : σ = m * (1 − P ) m, nel caso di 100 monete, é 50, P é la probabilità che si verifichi l’evento
testa, cioé, ancora nel caso delle monete non truccate, 50%. Quindi la dispersione teorica del
numero di teste, espressa come valore di σ , é: σ = 25 = 5
Si noti che i nuclei di un isotopo radioattivo hanno una probabilità –costante!- di decadere durante il
tempo di misura, ∆t, che é dato dal prodotto ∆t x P. P, questa volta, é la probabilità di decadimento
per unità di tempo, cioé: P=1/τ dove τ é la vita media dell’isotopo considerato. Essendo
normalmente il tempo di misura molto più piccolo della vita media, si può porre di solito P≅ 0.
Allora si ha: σ = m che può essere in pratica approssimato in: σ ≅ n .
Si noti attentamente che n non é il numero di decadimenti che sono effettivamente avvenuti nel
tempo ∆t ma il numero da noi misurato che é di solito moto più piccolo perché l’efficienza di
conteggio é di solito molto minore di 1. In analogia con le monete abbiamo, infatti, che ciò che
conta, dal punto di vista dell’errore statistico, non é il numero di monete che abbiamo lanciato ma,
quello delle monete che eventualmente, se il tavolo é piccolo, é rimasto sul tavolo ed é quello
effettivamente contato.
La regola della radice quadrata, così facilmente memorizzabile ha come fondamentale conseguenza
che l’errore relativo di origine statistica nella misura di n é semplicemente: σ /n = 1 / n . Ciò
fornisce immediatamente che se abbiamo nella misura di conteggio, per esempio, n = 100, l’errore
statistico relativo è del 10%, se n = 1000, esso è ≅ 3.3%, ecc. Si noti attentamente che ciò
rappresenta il limite minimo invalicabile per l’errore della misura di conteggio e che ad esso vanno
aggiunti gli eventuali errori sperimentali. Come regola generale, si ha che gli errori indipendenti di
una misura si sommano quadraticamente; cioè il valore finale dell’errore, espresso ancora come
deviazione standard σ, vale σ =
∑ σ i2
dove la somma è estesa a tutti i contributi, σi ,all’errore
finale imputabili a ogni possibile causa, ognuno dei quali deve essere valutato separatamente.
Quindi, se, per esempio, esiste una causa che produce un errore del 10% ,anche estendendo il
tempo di misura in modo che n sia molto maggiore di 100, non si otterrà, in pratica, alcun
miglioramento della precisione proprio a causa della regola della somma quadratica per gli errori.
Ricordiamo, infine, che nel linguaggio comune i termini precisione e accuratezza sono considerati
sinonimi. Nella teoria degli errori, invece, la precisione indica la dispersione dei dati ,ed é misurata
dal valore di σ , mentre l’accuratezza é misurata dalla differenza dal valore vero ( supposto noto )
del valore medio ottenuto nella misura e, di solito, dipende da un errore sistematico nel metodo di
misura.
Si noti attentamente che quando, come nel caso di un decadimento nucleare o del lancio delle
monete, si misura il numero di ripetizioni di un evento che ha probabilità di accadere costante e
nota, si può calcolare a priori il valore di σ tenendo conto della natura statistica del fenomeno. In
tutti gli altri casi, in generale, occorre conoscere la legge di distribuzione specifica della misura
considerata che permetta di prevedere a priori il valore della deviazione standard. Se ciò non é
possibile, la deviazione standard é ricavabile, a posteriori, dall’insieme stesso delle misure ottenute.
Questi argomenti sono piuttosto complicati. Nel tentativo di renderli un poco più
semplici,svolgiamo l’esempio di applicazione di una trattazione statistica in termini elementari ma
rigorosi alla produzione di un albero di mele. Vogliamo,cioè,ricavare i parametri che caratterizzino
la produzione di mele al fine ,per esempio, di un confronto significativo fra diverse piante.
Ovviamente, il primo dato significativo da ottenere é la produzione totale di mele ottenuta; cioè
semplicemente il peso totale, P, della produzione. Subito dopo, contando il numero n di mele,
otteniamo il valore medio, Pm = P/n , per il peso delle mele. Questa media, così ottenuta, é detta
media aritmetica, essa si ottiene dalla somma dei singoli valori attribuendo a ciascuno di essi lo
stesso peso statistico. Per misurare,ora, la dispersione nel peso delle mele, conviene fare riferimento
allo scarto, Pi - Pm , fra il peso Pi della generica iesima mela e il peso medio. Se però adesso
vogliamo valutare quale é la dispersione media in termini di scarto medio =
∑i Pi -Pm/n
Si ottiene: (∑i Pi − Pm ) / n = 0. Questo risultato, intuitivo, dipende direttamente dal fatto che
abbiamo scelto la media aritmetica per il peso medio, pertanto non possiamo fare riferimento a
questa procedura per avere una misura della dispersione del peso delle mele.
Dobbiamo fare invece ricorso allo scarto quadratico medio detto anche varianza che é definito
come la media del quadrato dello scarto, cioè: varianza =Σi (Pi – Pm)2/n. Infine, poniamo per la
deviazione standard:
σ=
∑i Pi− - Pm)2/n
che rappresenta,come si potrebbe dimostrare, l’espressione utilizzabile per la deviazione standard
precedentemente definita genericamente come scarto medio, nell’approssimazione che n >> 1.
A questo punto per potere proseguire nella descrizione statistica rigorosa della produzione di mele,
dobbiamo confrontare la distribuzione dei pesi delle mele con una distribuzione normale .
E’ al di là degli scopi di questi appunti, trattare con esattezza ciò che si intende per distribuzione
normale – detta anche Gaussiana o curva a campana -. Ci limitiamo a ricordare che la dispersione
dei valori ottenuti per una misura ( nel caso nostro: il peso delle mele del nostro albero) è nel caso
più frequente ,perciò detto anche normale, é governata da una legge di distribuzione, che ha la
forma già detta a campana e della quale non diamo la formula matematica, che ha come unico
parametro la deviazione standard. Questa curva assume una forma universale se la distribuzione
delle misure é espressa in funzione del rapporto dello scarto della misura dal valore medio, o
centrale, con il valore di σ .
La proprietà della distribuzione di Gauss in pratica si può ricavare dividendo l’insieme dei valori
dello scarto dal valore medio, espressi in unità di σ , in un numero finito di classi di larghezza
costante- per esempio, σ/2 o σ/4 − e ricavando da un’ apposita tabella numerica pubblicata in tutti i
libri di statistica quale sia la percentuale di misure dell’insieme che devono cadere, seguendo la
legge di distribuzione, all’interno di ogni classe.
In questo modo la legge é espressa sotto
forma di un istogramma composto da
elementi rettangolari che hanno per base
la larghezza, in unità di σ ,prescelta per
le classi ( per es.: σ/2 ) e per altezza il
valore che corrisponde al fatto che l’area
del rettangolo – base x altezza- indica la
frazione di misure contenute nella classe
stessa. In questo modo si ottiene che
l’area
totale
dell’istogramma,
considerando in teoria tutte le classi di
misure
incluse
anche
quelle
infinitamente lontane dal valore centrale,
vale 1. Con ciò intendendosi che la
probabilità che una misura fornisca un
valore qualsiasi, comprendendo anche
quelli più improbabili, é evidentemente
1.
In particolare,la distribuzione di Gauss
ha come risultato che circa il 70% delle
misure é compreso fra i valori relativi di
scarto + σ e –σ e il 97% delle misure con
scarto incluso fra ± 2σ.
In pratica, per completare il nostro
esercizio sulle mele, é sufficiente scegliere 8 classi ciascuna di larghezza σ/2 corrispondenti a un
intervallo di scarti dal valore medio centrale da -2σ a + 2σ , che include in pratica tutti i valori di
scarto per i pesi possibili; successivamente si contano le mele contenute in ogni classe e si divide
ciascun numero di contenuto per il valore del numero totale di mele prodotte dall’albero. Se il
nostro melo ha una distribuzione di pesi delle mele normale, questi numeri così ottenuti debbono
adattarsi ragionevolmente bene alle probabilità di occorrenza per ciascuna classe descritte dalla
distribuzione di Gauss.
Si ricorda che noi abbiamo applicato queste considerazioni statistiche alle misure con il C14. E’
fondamentale tenere presente che in quel caso, ricorrendo il caso di una misura di decadimento
radioattivo, il valore di σ può essere noto a priori dalle considerazioni statistiche sul numero di
conteggi e da eventuali cause di errore del metodo di misura, anche esse note a priori. Pertanto, non
é necessario ripeter una misura un elevato numero di volte, come invece é necessario nel caso della
pesata delle mele. Non esiste,infatti, una teoria che dia la possibilità di prevedere il valore di σ per
il nostro albero; tuttavia, come abbiamo visto, é necessario conoscere il valore di σ per eseguire il
confronto con la curva di distribuzione normale, pertanto il valore di σ deve essere determinato
sperimentalmente.










