10/04/2011
CONTINUITA’
www.liceocavalieri.it/public/classi/archiviorisorse%5CCONTINUITA
CONTINUITA’
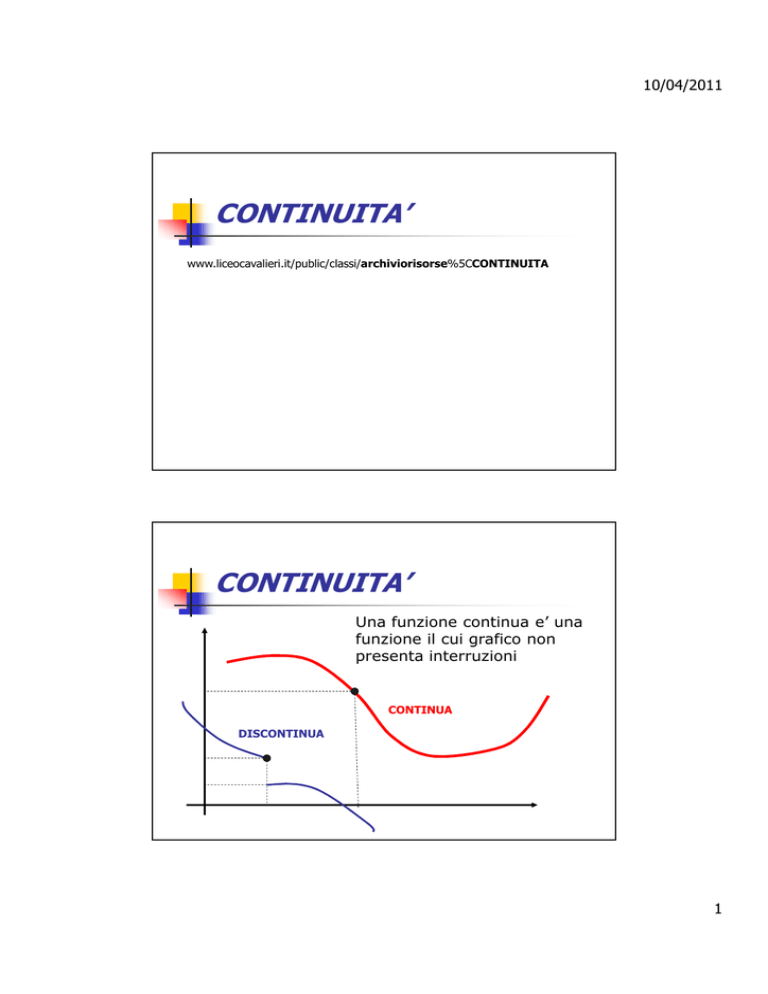
Una funzione continua e’ una
funzione il cui grafico non
presenta interruzioni
CONTINUA
DISCONTINUA
1
10/04/2011
CONTINUITA’
P
Yo=f(Xo)
Nel punto P(Xo,Yo) questa
funzione è continua: il limite
per x tendente a Xo è Yo,
che è anche il valore della
funzione
CONTINUA
Xo
CONTINUITA’
Questa è discontinua: il limite
sinistro e destro per x tendente a
Xo questi danno due valori diversi,
Yo e un altro, H. Il grafico compie
un salto pari a Yo-H
DISCONTINUA
Yo
H
Xo
2
10/04/2011
CONTINUITA’
Data f:D->R, e dato Xo punto del dominio D, allora
la funzione f si dice CONTINUA in Xo se il limite
per x tendente ad Xo di f(x):
• ESISTE
• E’ FINITO
• E’ UGUALE A f(Xo)
Ovvero, in formule:
Lim f ( x) = f ( xo )
x → xo
CONTINUITA’
Una funzione continua in tutti i punti di un
certo intervallo si dice CONTINUA SU
QUELL’INTERVALLO
3
10/04/2011
CONTINUITA’
Se una di queste clausole non è verificata
allora la funzione si dice discontinua in Xo.
CONTINUITA’
I punti di discontinuità vengono classificati
in tre specie
4
10/04/2011
CONTINUITA’
Se il limite sinistro e destro di f(x) per x tendente a
Xo:
• ESISTONO
• SONO FINITI
• SONO DIVERSI TRA LORO
Xo si dice punto di discontinuità di PRIMA SPECIE
CONTINUITA’
La funzione
y=INT(x) offre un
esempio di tale
discontinuità: tutti i
numeri interi sono
punti di discontinuità
di prima specie
1
2
3
5
10/04/2011
CONTINUITA’
CONTINUITA’
Se almeno uno dei due limiti, sinistro o destro, di
f(x) per x tendente a Xo:
• NON ESISTE…
• …OPPURE NON E’ FINITO
Xo si dice punto di discontinuità di SECONDA
SPECIE
6
10/04/2011
CONTINUITA’
La funzione y=ln(x)
offre un esempio di
tale discontinuità
nell’origine
CONTINUITA’
7
10/04/2011
CONTINUITA’
Se il limite per x tendente a Xo esiste, è finito, ma
è diverso della valore della funzione (oppure la
funzione non esiste in Xo)
Lim f ( x) ≠ f ( xo )
x → xo
Xo si dice punto di discontinuità di TERZA SPECIE,
o ELIMINABILE
CONTINUITA’
La discontinuità si dice eliminabile perché basta
alterare leggermente la definizione della funzione
ponendo:
f ( xo ) = Lim f ( x)
x → xo
Per rendere la funzione continua
8
10/04/2011
CONTINUITA’
Un esempio è la funzione:
senx
f ( x) =
x
Infatti non esiste per X=0, ma il limite per x
tendente a 0 è, come è noto, 1.
Basta quindi porre:
f(0)=1
E la funzione risulta continua anche in 0.
CONTINUITA’
9
10/04/2011
CONTINUITA’
Dove si trovano i punti di discontinuità di una
funzione?
• Nei punti esclusi dal dominio (che siano però
punti di accumulazione del dominio)
• Nei punti in cui l’argomento di un valore
assoluto cambia segno
• in altri casi particolari
CONTINUITA’
TEOREMA DI WEIERSTRASS
Una funzione continua su un intervallo chiuso
ammette sempre massimo e minimo assoluti
su quell’intervallo
10
10/04/2011
CONTINUITA’
MASSIMO
MINIMO
Una curva senza
salti, definita su
un intervallo, di
fatto può essere
racchiusa in un
rettangolo, la cui
altezza avrà per
estremi il
massimo e il
minimo della
funzione
CONTINUITA’
TEOREMA DI DARBOUX
Una funzione continua su un intervallo chiuso
assume almeno una volta tutti i valori
compresi tra il minimo e il massimo
11
10/04/2011
CONTINUITA’
TEOREMA DI DARBOUX
Potremmo enunciarlo anche così: se la funzione f è
continua sull’intervallo [a,b] e se il numero k è
compreso tra min(f) e max(f) su tale intervallo,
allora esiste un punto c appartenente ad [a,b] tale
che:
f(c)=k
CONTINUITA’
Graficamente è
abbastanza
evidente che, se
una curva è
continua, al
valore k
compreso tra
min e max deve
corrispondere un
valore c tra a e b
MASSIMO
k
MINIMO
a
c
b
12
10/04/2011
CONTINUITA’
TEOREMA DEGLI ZERI
Se f è una funzione continua su un intervallo
chiuso e se su tale intervallo la funzione
cambia segno, allora esiste almeno un punto
dell’intervallo in cui la funzione si annulla
CONTINUITA’
TEOREMA DEGLI ZERI (altra versione)
Se f è una funzione continua su un intervallo
chiuso e se su tale intervallo la funzione
cambia segno, allora l’equazione:
f(x)=0
Ammette almeno una soluzione in tale
intervallo
13
10/04/2011
CONTINUITA’
E’ una conseguenza del teorema di Darboux; infatti
se la funzione cambia segno sicuramente il
massimo sarà un numero positivo e il minimo un
numero negativo: e siccome 0 è sempre compreso
tra un numero positivo e uno negativo, allora la
funzione deve per forza assumere il valore 0.
14










