LO STATO VETROSO

CorsodiMacromolecole
LOSTATOVETROSO
Perstudiarelostatofisicodelsistemaedintrodurrequindiladiscussionesullo
statovetrososipuòdescriverecomeessovariaalvariaredellatemperatura.
Ø partendodalcristalloeriscaldandolo:
aumentanolevibrazionireticolari,idifettieilvolumespecifico.Quando
l’energiaèsufficientementealtalafusioneavvieneallatemperatura
termodinamicadifusioneT°f.
Ø partendoinvecedalfuso(materialeamorfo)eraffreddandolo:
bisognaprendereinconsiderazioneilparametrotempo
• Seilpolimeroèregolareeilprocessoavvieneinuntempo
sufficientementelungoavvienelacristallizzazione.
• Seilprocessoavvienerapidamentesipossonoavereduestatimetastabili:
- Liquidosottoraffreddato:faseliquidachepermanealdisottodella
T°f.
- Vetro:solidoamorfochemantieneildisordinedellafaseliquida.
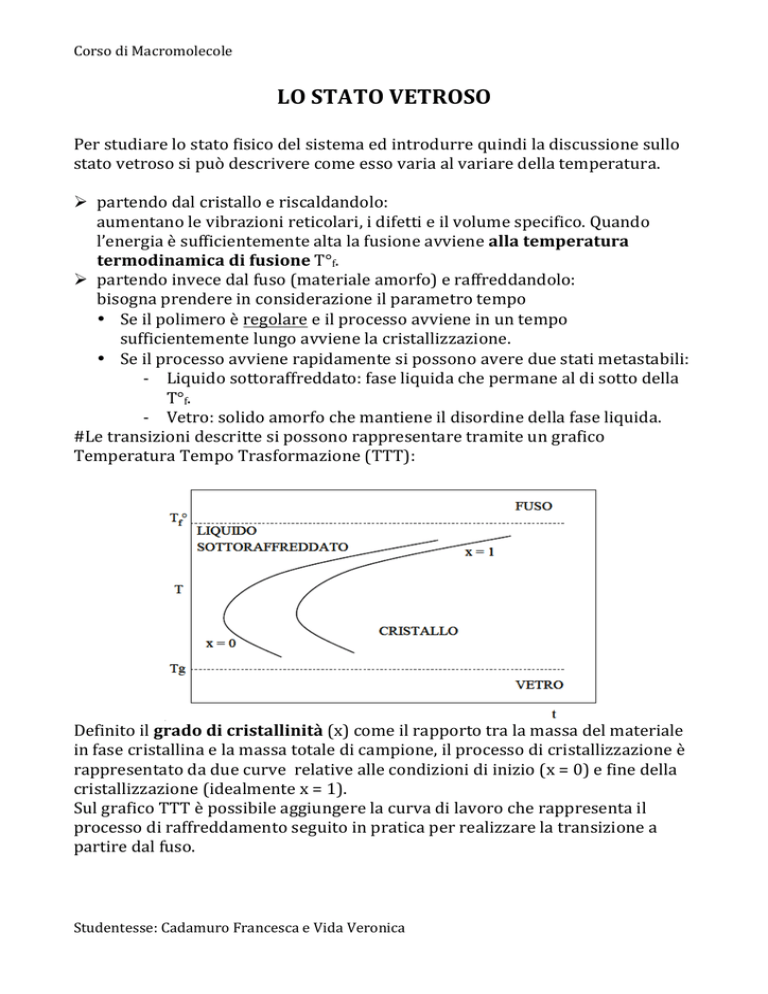
#Letransizionidescrittesipossonorappresentaretramiteungrafico
TemperaturaTempoTrasformazione(TTT):
Definitoilgradodicristallinità(x)comeilrapportotralamassadelmateriale
infasecristallinaelamassatotaledicampione,ilprocessodicristallizzazioneè
rappresentatodaduecurverelativeallecondizionidiinizio(x=0)efinedella
cristallizzazione(idealmentex=1).
SulgraficoTTTèpossibileaggiungerelacurvadilavorocherappresentail
processodiraffreddamentoseguitoinpraticaperrealizzarelatransizionea
partiredalfuso.
Studentesse:CadamuroFrancescaeVidaVeronica
CorsodiMacromolecole
Tc
Persemplificarelatrattazionesipuòassumerechelavelocitàdiraffreddamento
siacostante(lacurvadilavoroèunaretta).
Nelgraficosottoriportatosonorappresentatetrediversevelocitàdi
raffreddamento:
A=velocitàdiraffreddamentoalta
B=velocitàcritica
C=velocitàdiraffreddamentobassa
Siosservachealdisottodellavelocitàcriticanonpuòavvenireilprocessodi
cristallizzazione.
TRANSIZIONEVETROSA
Èunatransizionedinaturacineticalegataallamaggioreominorefacilitàdi
movimentirotazionalietraslazionalidellemacromolecole,dovutaalladiversa
strutturadivetroeliquidosottoraffreddato.
Studentesse:CadamuroFrancescaeVidaVeronica
CorsodiMacromolecole
• Liquidosottoraffreddato:sonopermessimovimentirotazionalie
traslazionali.
• Vetro:imovimentideglielementistrutturalisonoimpediti.Èancora
permessatuttaviaunacertamobilitàcheportaastativetrosicondiverse
proprietàaspettandotempilunghi(“INVECCHIAMENTOFISICO”)
Unaproprietàcaratteristicadellostatovetrosoèlaviscosità(𝜂)chehaforma:
!
𝜂 = 𝑘𝑒 !" dove:
k=costanteempirica
B=energiadiattivazionedeimovimentistrutturali
L’andamentodellacurvasperimentaleèdatodall’equazionediCOHEN–
TUMBUL
𝐵′
log 𝜂 = 𝐴 +
(𝑇 − 𝑇! )
dove:
A=lnk.
Sesivuolecaratterizzareilsistemainbasealgradod’ordinedellasuastruttura
siintroduceilparametrod’ordineZ(T,P)ilqualeèmaggioreabasse
temperature.
Seneosserval’andamentoconilseguentegraficoilqualerappresentaun
processodiraffreddamentoapressionecostanteseguitodauntrattamento
isotermo.
• T=T0:ilsistemapolimeroèinequilibrioconl’ambienteesterno.
• T0àT*:lastrutturaevolvemantenendosiinequilibrioconl’esternofino
allatemperaturacriticaalpuntoT*(T*=Tg).
Studentesse:CadamuroFrancescaeVidaVeronica
CorsodiMacromolecole
• T*àT2:ilsistemanonpuòadeguarsiallecondizioniesterne.
• T2=costante:ilsistemaevolveversoilvalorediequilibriodiZ(T,P).
Siccomeilvetrononèunostatodiequilibriotermodinamico,essononha
condizionitermodinamichebendefinite.IlvalorediTgdipendeinfattidalla
cineticadelsistemaandandoadaumentareall’aumentaredellavelocitàdi
raffreddamento.
DETERMINAZIONEDELLATRANSIZIONEVETROSA
Puòesseredeterminataapartiredamisuredi:
• VOLUMESPECIFICO
• CONTENUTOENTALPICO
• MODULOELASTICO
Volumespecificoecontenutoentalpicosonocorrelatiallastruttura
intermolecolareeallesuevariazioniconlatemperatura.
DATISPERIMENTALI
Sidefinisceilcoefficientediespansione:
αV =
1 ⎛ ∂V ⎞
⎜
⎟
V ⎝ ∂T ⎠ P EssosubisceunabruscavariazionenelvalorenumericoallaTg.
Siccomelemisuresperimentalisieffettuanoperviacalorimetricaedèpiù
comodooperareapressionecostante,sidefinisceilcalorespecificoapressione
costanteCp:
⎛ ∂H ⎞
CP = ⎜
⎟
∂
T
⎝
⎠P Essosimisuratramiteilcalorimetrodifferenzialeascansione.
MODULOELASTICO:descrivelatendenzadiunoggettoadeformarsi
elasticamentequandosiapplicaunaforza.
IlMODULODIYOUNG(E)èilmodulodielasticitàlongitudinaleesidefinisce
come:
E=forza/deformazione
Diconseguenzaunmaterialemoltorigidochesideformapocoavràunmodulo
diYoungmoltoalto.
Studentesse:CadamuroFrancescaeVidaVeronica
CorsodiMacromolecole
PARAMETRICHEINFLUENZANOILVALORENUMERICODELLATRANSIZIONE
VETROSA
Iparametrisidividonoindueclassi:
• PARAMETRIINTERNI(dovutiallanaturamacromolecolare)chesono:
1. FLESSIBILITA’DELLACATENAMACROMOLECOLARE:viene
miglioratadall’inserimentodi:
- monomeririgidi
- sostituentilateralirigidiestericamente
ingombrati
2. FORZEDIINTERAZIONETRALEUNITA’MOLECOLARI:forzefortidi
coesione(dovuteadesempioalegamiaidrogenoogruppipolari)
fannoaumentarelaTg.
• PARAMETRIESTERNI(controllabili)chesono:
1. MASSAMOLECOLARE:ladipendenzadiTgdaessaèdata
dall’equazionediFLORY–FOX.Lamassamolecolareinizialmente
aumentarapidamenteconlamassaperpoirallentarelavelocitàdi
crescitafinoaunvalorecostante
2. INTRODUZIONEDIUNITA’CONFUNZIONALITA’>2:
- catenenonlineari:aparitàdipesoTg
diminuisceall’aumentaredelleramificazioni
- reticolazione:determinaunaumentodiTg
3. PARZIALECRISTALLINITA’:all’aumentaredelsuogradoaumenta
Tg(aumentanoivincolifisicialmovimento)
4. EFFETTODIPLASTIFICAZIONE:aggiungendounprodottodetto
“plastificante”dotatodiTgminoresiabbassalaTgdelpolimeroper
renderlopiùmodificabile.
Studentesse:CadamuroFrancescaeVidaVeronica