Valutazione dell’esistente ed adeguamento
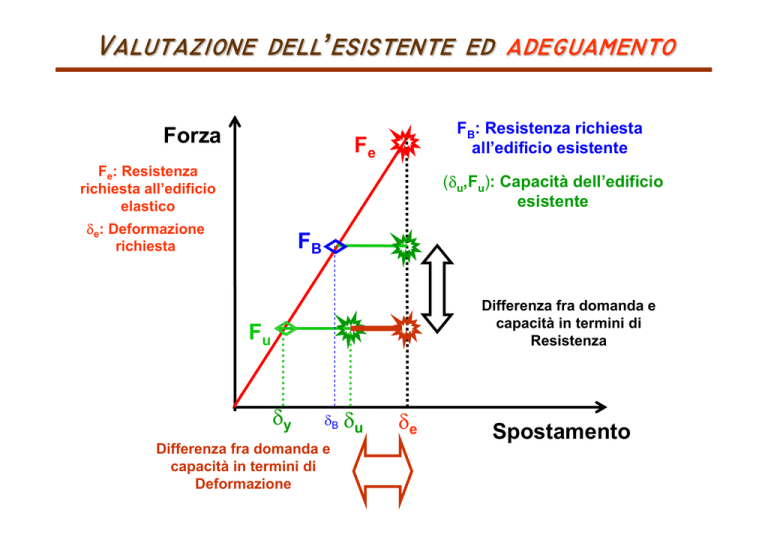
Forza
FB: Resistenza richiesta
all’edificio esistente
Fe
Fe: Resistenza
richiesta all’edificio
elastico
(δu,Fu): Capacità dell’edificio
esistente
δe: Deformazione
richiesta
FB
Differenza fra domanda e
capacità in termini di
Resistenza
Fu
δy
δB
Differenza fra domanda e
capacità in termini di
Deformazione
δu
δe
Spostamento
Tipo di intervento
• Sono previsti due tipi di intervento
– Miglioramento
– Adeguamento
• Miglioramento
– l’esecuzione di una o più opere riguardanti singoli
elementi strutturali dell’edificio allo scopo di conseguire
un maggior grado di sicurezza
• Adeguamento
– l’esecuzione di un complesso di opere che risultino
necessarie per rendere l’edificio atto a resistere alle azioni
sismiche di normativa
Norme tecniche per le costruzioni - D.M. 14 settembre 2005
Gazzetta Ufficiale n. 222 del 23 settembre 2005 - Supplemento Ordinario n. 159
Cap. 9 – COSTRUZIONI ESISTENTI
9.2. CRITERI GENERALI
9.2.1. VALUTAZIONE DELLA SICUREZZA
La valutazione della sicurezza deve permettere di stabilire se:
- l’uso della costruzione possa continuare senza interventi;
- l’uso debba essere modificato nel verso di un minore cimento statico
(declassamento);
declassamento
- debba essere necessario procedere ad aumentare la capacità portante
(consolidamento);
- debba essere necessario procedere a ripristinare la capacità portante
preesistente ad un danno (riparazione)
riparazione
- debba essere necessario adeguare la sicurezza dell’opera, in tutto od
in parte, alle prescrizioni della presente norma (adeguamento);
SCELTA DELL’INTERVENTO
TIPO D’INTERVENTO
DEMOLIZIONE E/O
RICOSTRUZIONE
AUMENTO DELLA
CAPACITÀ DI
PRESTAZIONE
RIDUZIONE DELLA
DOMANDA DI
PRESTAZIONE
SCELTA DELL’INTERVENTO
TIPO D’INTERVENTO
AUMENTO DELLA
CAPACITÀ DI
PRESTAZIONE
MODIFICA
DELL’ORGANISMO
STRUTTURALE
TECNICA
Aggiunta di nuovi elementi resistenti come, ad esempio,
pareti in c.a., pareti di controvento in acciaio, cordoli di
incatenamento in c.a. per strutture murarie…
Saldatura di giunti tra corpi fabbrica, ampliamento dei
giunti, eliminazione di elementi particolarmente
vulnerabili, eliminazione di eventuali piani “deboli”…
Eventuale trasformazione di elementi non strutturali in
elementi strutturali.
SCELTA DELL’INTERVENTO
TIPO D’INTERVENTO
TECNICA
RIDUZIONE DELLA
DOMANDA DI
PRESTAZIONE
RIDUZIONE DELLE
MASSE
Sostituzione di componenti strutturali
con
componenti
strutturali
ugualmente resistenti ma più leggere
Eliminazione
o
sostituzione
di
componenti non strutturali ed impianti
Cambio della destinazione d’uso
TECNICA
PROTEZIONE
PASSIVA
Isolamento antisismico
Dissipazione passiva
PROGETTAZIONE DELL’INTERVENTO
Generalmente, per effettuare la scelta della tecnica
dell’intervento, alla capacità di resistenza delle strutture va
associata anche una valutazione della capacità di duttilità
degli elementi strutturali e della struttura nel suo complesso.
A seguito dell’intervento, solo nel caso dell’utilizzo di tecniche
di protezione passiva (isolamento antisismico e
dissipazione passiva) si può garantire un comportamento
elastico alla struttura in quanto le plasticizzazioni sono
localizzate in alcuni elementi specifici appositamente scelti e
collocati all’interno della struttura.
Strategia di intervento
CARATTERISTICHE PECULIARI DELLE STRATEGIE DI INTERVENTO
• Intervento locale su componenti strutturali
La capacità di deformazione
degli elementi strutturali
può essere incrementata
passando da modi di rottura
fragili a modi di rottura
duttili
• Intervento globale sul sistema strutturale
L’intervento tende a limitare la
domanda di deformazione nei
componenti fragili aumentando
la rigidezza laterale, riducendo
la massa, introducendo isolatori
o dissipatori
Interventi globali
CARATTERISTICHE PECULIARI DELLE STRATEGIE DI INTERVENTO
• Inserimento di controventi metallici
• Tecniche di protezione sismica:
Isolamento alla base
• Inserimento di pareti sismoresistenti
Controventi dissipativi
ISOLAMENTO SISMICO
OSCILLAZIONI DI UN EDIFICIO
A BASE FISSA ED ISOLATO
Struttura convenzionale
Struttura isolata alla base
Nelle oscillazioni della struttura si deformano soprattutto gli isolatori mentre
la struttura rimane quasi al suo posto e subisce piccole deformazioni.
Protezione Sismica mediante l’utilizzo di ISOLAMENTO alla base
Sono dispositivi a rigidezza orizzontale fortemente differente da quella della struttura in
cui vengono inseriti. La tecnica consiste nella sconnessione tra la sovrastruttura e la
fondazione tale da ottenere una conveniente variazione nella risposta dinamica della
struttura rispetto a quella a “base fissa”
Isolatori ELASTOMERICI
con acciaio interposto
Isolatori a SCORRIMENTO
e/o ATTRITO
Isolatori in
acciaio-PTFE
Spostamento laterale fino a 1,5
volte l’altezza dell’isolatore!!!!!
CONTROVENTI DISSIPATIVI
OSCILLAZIONI DI UN EDIFICIO
A BASE FISSA E CON DISSIPATORI
Struttura convenzionale
Struttura con controventi
dissipativi
Nelle oscillazioni della struttura si deformano anche i dissipatori che nella
deformazione dissipano parte dell’energia fornita dal terremoto.
Protezione Sismica mediante sistemi di DISSIPAZIONE aggiuntiva
Trasformano in calore la maggior parte dell’energia trasmessa dall’evento
sismico alla struttura. Possono essere di tipo ricentrante o non ricentrante. La
dissipazione può ottenersi sostanzialmente in tre modi:
Per SNERVAMENTO del
dissipatore (Metallic Dampers)
Per ATTRITO
(Friction Dampers)
Per VISCOSITÀ di un fluido o di un materiale
(Viscous Fluid, Viscoelatic Dampers)
Essi sono indicati per l’adeguamento sismico degli edifici, poiché
l’inserimento di braccia di controvento con dissipatori, limita lo
spostamento di interpiano e di conseguenza nel controllo del danno.
Esempio di
dispositivo a
plasticizzazione
Esempio di dispositivo
ADAS
viscoelastico
Esempio di dispositivo
fluido-viscoso
Esempio di dispositivo
a attrito
FILOSOFIA
DUNQUE È UNA TECNICA DI PROTEZIONE PASSIVA CHE NASCE PER LE STRUTTURE
NUOVE MA SI ADATTA MOLTO BENE (FORSE MEGLIO) ALLE STRUTTURE ESISTENTI .
A DIFFERENZA DELL’ISOLAMENTO ALLA BASE,
CHE PUNTA A RIDURRE L’ENERGIA SISMICA CHE ENTRA NELLA STRUTTURA,
I CONTROVENTI DISSIPATIVI LASCIANO TALE ENERGIA IMMUTATA
(POSSONO ADDIRITTURA FARLA CRESCERE)
MA PUNTANO AD AUMENTARE IN MODO DRASTICO LA DISSIPAZIONE DI ENERGIA
LA DISSIPAZIONE DI ENERGIA NON È CONSEGUITA ATTRAVERSO IL DANNEGGIAMENTO
DELLA STRUTTURA (DUTTILITÀ) ANZI LA PRINCIPALE FINALITÀ CHE CI SI PONE È
PROPRIO QUELLA DI PROTEGGERE LA STRUTTURA.
CIÒ AVVIENE RACCOGLIENDO, ATTRAVERSO ELEMENTI DI RIGIDEZZA PREVALENTE
RISPETTO A QUELLA DELLA STRUTTURA (I CONTROVENTI)
L’ENERGIA SISMICA IN ECCESSO E INDIRIZZANDOLA SU APPOSITI ELEMENTI DESTINATI
A DISSIPARLA (I DISSIPATORI).
L’IDEA È DUNQUE FRENARE MANTENENDO ELASTICA LA STRUTTURA (CHE SIA IN C.A.
O ACCIAIO) “BRAKING RATHER THAN BREAKING” APPUNTO.
Protezione sismica mediante controventi dissipativi
STRATEGIE DI PROGETTAZIONE
Le strategie di progettazione sono individuate dall’incrocio tra i livelli di azione ed
i livelli di prestazione:
TESTO UNITARIO
Pn≥1
OI
SLD
O
SV
SLU
PC
FEMA 356
50% in 50anni
30% in 50anni o 50% in 100 anni
STRATEGIA DI BASE
PER LA PROGETTAZIONE
(per il Testo Unitario:
Costruzioni di Classe 1)
20% in 50anni
10% in 50anni
5% in 50 anni o 10% in 100 anni
2% in 50anni
Pn≥1
OI
SLD
O
SV
SLU
PC
Obiettivi per i quali
sono indicati i
controventi dissipativi
50% in 50anni
30% in 50anni o 50% in 100 anni
20% in 50anni
10% in 50anni
5% in 50 anni o 10% in 100 anni
2% in 50anni
STRATEGIA POTENZIATA
PER LA PROGETTAZIONE
(per il Testo Unitario:
Costruzioni di Classe 2)
PRINCIPIO DI D’ALEMBERT
EQUAZIONE DEL MOTO per un oscillatore ELASTO-VISCOSO LINEARE
d 2 xg
2
d u
du
M 2 + C + Ku = −M 2
dt
dt
dt
essendo xg lo spostamento del
terreno (ground)
ovvero secondo J. Le Rond D’Alembert (1717-1783)
Forze d’inerzia
o “Inertia”
Eccitazione sismica
o “Earthquake”
f I (t ) + f D (t ) + f S (t ) = f E (t )
Forze di deformazione o “Strain”
Forze di viscosità o “Damping”
D’Alembert
RISPOSTA DI OSCILLATORI SMORZATI A FORZANTI ARMONICHE
du
d 2u
Equazione del moto: M
+ C + Ku = p ⋅ sen(ω f t )
2
dt
dt
Eq. del moto in forma canonica:
d 2u
du
2
2
+
2
ξω
+
ω
u
=
ω
uo sen(ω f t )
2
dt
dt
Frequenza circolare
dell’oscillatore: ω =
K
M
Rapporto di smorzamento
c
dell’oscillatore:
ξ=
2Mω
Spostamento statico
dell’oscillatore: u =
o
p
K
Fattore di amplificazione
umax
dinamica:
D=
uo
Frequenza circolare
ωf
adimensionalizzata
β=
della forzante:
ω
Fattore di amplificazione dinamica D
25
20
ξ=2%
15
ξ=5%
10
ξ=10%
ξ=20%
5
0
0
0.5
1
1.5
β
2
2.5
3
D’Alembert
DECOMPOSIZIONE DEL SISMA IN FORZANTI ARMONICHE ELEMENTARI
0.6
Terremoto del Friuli - Tolmezzo NS
6 maggio 1976
Magnitudo ML=6,5
0.4
a [g]
0.2
0
-0.2
-0.4
0
2
4
6
8
0.2
0.15
0.1
0.05
0
12
14
16
18
20
Accelerogramma
Spettro di Fourier - ampiezza
Ampiezza armoniche Fourier
0.25
10
t [s]
10
-1
10
T [s]
0
10
1
0.4
10
0.35
9
8
0.3
7
ξ=5%
0.25
6
0.2
5
ξ=20%
4
0.15
3
0.1
2
0.05
0
1
10
-1
10
T [s]
0
10
0
1
Fattore di amplificazione dinamica D
Ampiezza armoniche Fourier
D’Alembert
CONVOLUZIONE SISMA - OSCILLATORI CON T=0,5s E ξ=5%-20%
D’Alembert
CONVOLUZIONE SISMA-OSCILLATORI A DIVERSO SMORZAMENTO
Dalla convoluzione tra terremoto scomposto in forzanti armoniche e oscillatori elementari a diverso
periodo e due valori fissi di smorzamento si ricavano gli spettri della risposta elastica in spostamenti
e pseudo-accelerazioni per gli oscillatori elementari con i due valori di smorzamento.
14
2
ξ=5%
Pseudo-accelerazioni [g]
Spostamenti [cm]
12
10
8
6
4
ξ=20%
2
0
0
1
2
T [s]
3
Spettro di risposta elastico in
spostamenti
4
1.5
ξ=5%
1
ξ=20%
0.5
0
0
1
2
T [s]
3
Spettro di risposta elastico in
pseudo-accelerazioni
4
EFFETTO DELLO SMORZAMENTO AGGIUNTIVO
Aumento di periodo: T =
T ζ =0
1− ξ 2
Riduzione delle accelerazioni
10
5 + 100ξ
η=
ξ
η
0,05
100%
0,10
82%
0,20
71%
0,25
58%
0,30
55%
Spettro di risposta elastico per la componente orizzontale dell’accelerazione sismica
(Zona sismica 1 – Suolo A – Smorzamento variabile tra il 5% ed il 30%) - DM 14/09/2005
CONTROVENTI ELASTICI
Controventi elastici vs Isolamento
Controventi
Isolamento
Spettro di risposta elastico per la componente orizzontale dell’accelerazione sismica
(Zona sismica 1 – Suolo A – Smorzamento convenzionale del 5%) - DM 14/09/2005
CONTROVENTI DISSIPATIVI
Effetto dello smorzamento aggiuntivo
Aumento di periodo: T =
T ζ =0
1− ζ 2
Riduzione delle accelerazioni
η=
Controventi
dissipativi
10
≥ 0,55
5 + 100ζ
ζ
η
0,05
100%
0,10
82%
0,20
71%
0,25
58%
0,30
55%
Spettro di risposta elastico per la componente orizzontale dell’accelerazione sismica
(Zona sismica 1 – Suolo A – Smorzamento variabile tra il 5% ed il 30%) - DM 14/09/2005
Confronto tra un Telaio normale e Telai con protezione sismica
Isolatori alla Base
0
2
4
Dissipatori
6
8
Telaio Normale
10
12
14
16
18
0,6
0,5
0,4
A
cc 0,3
el 0,2
er 0,1
a
0
zi
o -0,1
n -0,2
-0,3
-0,4
In questo punto la struttura subisce una forza
orizzontale pari a metà del suo peso!!!
Accelerogramma di Tolmezzo (UD) Friuli 1976
20
Tempo [sec.]
0
2
0
2
4
6
8
10
12
10
12
14
16
18
20
0,7
Isolatori alla Base
0,6
0,5
0,4
0,3
0,2
0,1
0
-0,1
-0,2
-0,3
-0,4
4
6
8
14
16
18
20
0,8
Dissipatori
Spostamento[cm]
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
-0,8
0
5
4
3
2
1
0
-1
-2
-3
-4
-5
v
2
4
6
8
10
12
14
16
18
20
Telaio Normale
CONFIGURAZIONE DEI CONTROVENTI
Possibili configurazioni per i controventi:
Eccentrici
Concentrici
e
aX
aX
e
e
aV
aK
e
aK
aK
aλ
e
aY
PROGETTAZIONE DEI CONTROVENTI DISSIPATIVI
La progettazione deve comunque essere iterativa. Essa può essere articolata nei
seguenti passi:
1.
definizione delle proprietà strutturali dell’edificio e analisi strutturale
dell’edificio sia per carichi verticali che per forze sismiche;
2.
scelta della capacità di dissipazione (in termini di fattore di smorzamento)
che si vuole conferire al sistema;
3.
scelta della disposizione dei controventi dissipativi compatibilmente ai
vincoli architettonici;
4.
scelta delle caratteristiche meccaniche dei singoli dissipatori (in termini
di legame “forza-deformazione”) in modo da ottenere la capacità di
dissipazione desiderata;
5.
verifica delle reali prestazioni del sistema strutturale.
Le proprietà del sistema strutturale devono essere aggiornate di ciclo in ciclo, a seguito
del cambiamento delle caratteristiche meccaniche dei controventi.
DISPOSITIVI DI DISSIPAZIONE ENERGETICA
In accordo con la Normativa americana (FEMA 356 – Punto 9.3.3) si classificano i
dispositivi di dissipazione energetica in:
• dispositivi a dissipazione “dipendente dallo spostamento”
La risposta ciclica è indipendente dalla velocità relativa tra le due estremità del
dispositivo e dalla frequenza di eccitazione; il legame forza-spostamento
dipende dallo spostamento relativo tra le due estremità del dispositivo.
I dispositivi esibiscono comportamenti isteretico bilineare o trilineare, elastoplastico o rigido plastico (attritivo)
• dispositivi a dissipazione “dipendente dalla velocità”
La risposta ciclica è dipendente dalla velocità relativa tra le due estremità del
dispositivo e dalla frequenza di eccitazione.
I dispositivi sono basati su solidi visco elastici (polimeri siliconici), fluidi visco
elastici, fluidi viscosi
bilineare o trilineare isteretico, elasto-plastico o
rigido plastico (attritivo)
• dispositivi “di altro tipo”: dispositivi con capacità ricentranti (SMA, Molle+attrito)
DISPOSITIVI DI DISSIPAZIONE ENERGETICA
Per la caratterizzazione meccanica dei dissipatori, se ne considera il tipo di comportamento nella
direzione lungo la quale manifestano il comportamento dissipativo.
Tipo
dispositivi a
dissipazione
“dipendente
dallo
spostamento”
dispositivi a
dissipazione
“dipendente
dalla
velocità”
Dissipatore
Elasto-plastico
(EP)
Attritivo (FR)
Viscoso
lineare (VL)
Elasto-viscoso
lineare (VE)
Parametri meccanici
k1 Rigidezza elastica
α Fattore d’incrudimento
µ
duttilità
Fs Forza di scorrimento
cd Coefficiente di
viscosità
k d Rigidezza elastica
η Fattore di perdita
“loss factor”
Modello reologico
Schema di comportamento dei vari tipi di controvento
Meccanismo di plasticizzazione dei controventi eccentrici
Analisi della risposta di sistemi di controvento
Robert Tremblay, “Inelastic seismic response of steel bracing members”, Journal of Constructional Steel Research 58 (2002) 665–701
Controvento di strutture mediante elementi BRB
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
I “dispositivi elasto-plastici” dissipano energia attraverso le deformazioni inelastiche
dei metalli che, superato un prefissato livello di carico, si plasticizzano.
Essi sono generalmente realizzati mediante piatti di spessore limitato generalmente
conformati in modo tale che il materiale si plasticizzi in modo uniforme.
PROPRIETÀ
•
•
•
buona stabilità dei cicli di
deformazione
problemi di fatica per elevato
numero di cicli di entità ridotta
discreta sensibilità alle variazioni di
temperatura
(in
caso
di
temperature
molto
basse
il
comportamento dell’acciaio da
duttile diventa fragile)
CICLO DI ISTERESI DI UN
DISSIPATORE IN ACCIAIO
Elementi meccanici di dissipazione
Amplificazione dell’effetto di dissipazione
Analisi di telai con controventi ed elementi dissipativi in alluminio
D. C. RAI1, B. J. WALLACE2 , “Aluminium Shear-Links For Enhanced Seismic Resistance”, Earth. Engng. Struct. Dyn. 27, 315-342 (1998)
Amplificazione del movimento di cinematismi
M.C. Constantinou, P. Tsopelas, Toggle-Brace-Damper Seismic Energy Dissipation Systems, J. of Struct. Eng., Vol. 127, No. 2, February, 2001.
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
LEAD EXTRUSIONS DAMPERS
Robinson e
Greenbank (1976).
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
SUMITOMO FRICTION DAMPER
Costituito da un pistone
ricoperto da cuscinetti
frenanti in rame che scorre
all’interno di un cilindro in
acciaio (Aiken e Kelly, 1990)
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
DISSIPATORI A TELAIO
Dissipatori a telaio in
acciaio conformati in modo
da mantenere sempre in
trazione i controventi (Tyler
1985, Ciampi 1989, 1993).
Tyler (1985)
Ciampi (1989, 1993)
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
SLIDING BOLTED JOINT
Connessioni realizzate con
piastre dotate di fessure in
cui i bulloni possono
scorrere. Le superfici sono
acciaio/acciaio o
acciaio/ottone. (Fitzgerald,
1989)
DISSIPAZIONE “DIPENDENTE DALLO SPOSTAMENTO”
X-BRACED FRICTION DAMPER
I controventi lavorano solo a
trazione; sono collegati tra di
loro da un telaio snodabile e
all’intersezione c’è un nodo
con un cuscinetto ad attrito
(Pall e Marsh, 1982).
Elementi di controvento con dissipazione ad attrito
T. Balendra, C.H. Yu, F.L. Lee, “An economical structural system for wind and earthquake loads”, Engineering Structures 23 (2001) 491–501
Analisi sperimentale di croci di controvento con dissipatori
M.R. Maherii, R. Kousari,, “Pushover tests on steel X-braced and knee-braced RC frames”, Engineering Structures 25 (2003) 1697–1705.
DISSIPAZIONE “DIPENDENTE DALLA VELOCITÀ”
I “dispositivi visco-elastici” sono realizzati da copolimeri o sostanze vetrose che
dissipano energia quando sottoposti a deformazioni di taglio.
Il dispositivo più comune consiste di strati di materiale visco-elastico confinati con piatti
di acciaio: la dissipazione energetica si ha quando la vibrazione della struttura induce un
movimento relativo tra i piatti esterni e quelli interni.
PROPRIETÀ
•
•
•
discreta sensibilità alle variazioni di
temperatura (al crescere della
temperatura si ha una riduzione di
rigidezza e smorzamento)
discreta sensibilità della forma del
ciclo con il livello di deformazione
difficoltà nel conseguire rigidezze
elevate
CICLO DI UN DISSIPATORE
VISCO-ELASTICO
DISSIPAZIONE “DIPENDENTE DALLA VELOCITÀ”
CYLINDRICAL VISCOUS LIQUID DAMPER
Dispositivi prodotti dalla
TAYLOR, mutuati
dall’ingegneria meccanica
dove erano già usati per il
controllo di impulsi e vibrazioni
(Harris e Crede, 1976).
DISSIPAZIONE “DIPENDENTE DALLA VELOCITÀ”
DISSIPATORI VISCO-ELASTICI
Strato di materiale
visco-elastico tra due
profilati a T.
Esperimenti su strutture con dissipatori viscoelastici
K. Chang, Y. Lin, Seismic Response of Full-Scale Structure with Added Viscoelastic Dampers, J. of Struct. Eng., Vol. 130, No. 4, April 1, 2004
Test su torri a più piani con dissipatori viscoelastici
K.W.Min a, J. Kim, Sang-Hyun Lee “Vibration tests of 5-storey steel frame with viscoelastic dampers”, Engineering Structures 26 (2004) 831–839
ALTRI TIPI DI DISPOSITIVI
I dispositivi in lega a memoria di forma sono realizzati mediante fili di lega a memoria
di forma. Il comportamento isteretico non è dovuto ad un meccanismo di dislocazione
come per l’acciaio ma ad una trasformazione di fase (da austenite a martensite).
PROPRIETÀ
•
•
•
•
•
•
possibilità
di
limitare
le
deformazioni residue
stabilità dei cicli di deformazione
buona resistenza a fatica per cicli di
entità ridotta
scarsa sensibilità alle variazioni
ambientali di temperatura
difficoltà nel conseguire rigidezze
elevate
costo elevato
CICLO DI UN DISSIPATORE IN
LEGA A MEMORIA DI FORMA
ALTRI TIPI DI DISPOSITIVI
DISSIPATORI IN LEGA A MEMORIA DI FORMA (Shape Memory Alloy)
Dispositivo costituito da
fili in SMA-austenite ed
elementi in acciaio
(Dolce, Marnetto, 2000).
SISTEMI AD UN GRADO DI LIBERTÀ
Schema di telaio ad 1 grado di libertà con controvento
Telaio multi-piano e
multi-campata
Analisi
modale
Telaio ad 1 grado di
libertà
Massa concentrata
MODO DI VIBRARE PRINCIPALE DI UN TELAIO
MULTI-PIANO E MULTI-CAMPATA
TELAIO AD 1 GRADO DI LIBERTÀ EQUIVALENTE
AL MODO DI VIBRARE PRINCIPALE DEL TELAIO
SISTEMI AD UN GRADO DI LIBERTÀ
Schema di telaio ad 1 grado di libertà con controvento
Analogamente, con opportuni accorgimenti, è possibile ridurre un telaio multi-piano e multi-campata
con controventi elastici o dissipativi ad un telaio ad 1 grado di libertà dotato di un singolo
controvento.
TELAIO AD 1 GRADO DI LIBERTÀ CON
CONTROVENTO ELASTICO
TELAIO AD 1 GRADO DI LIBERTÀ CON
CONTROVENTO DISSIPATIVO
CONTROVENTI ELASTICI
Equivalenza tra il telaio ad 1 grado di libertà con CONTROVENTO ELASTICO e
l’oscillatore elementare.
TELAIO AD 1 GRADO DI LIBERTÀ CON
CONTROVENTO ELASTICO
OSCILLATORE ELEMENTARE
CONTROVENTI ELASTICI
Comportamento statico incrementale del sistema telaio+controvento
F
Sistema
Telaio+controvento
F
Fy sistema
Controvento
elastico
Fy telaio
Telaio
KH sistema
O
dy telaio
d
d
CONTROVENTI ELASTICI
Comportamento ciclico del sistema composto telaio+controvento per telaio che
Sistema
rimane ELASTICO
Telaio+controvento
Nota bene:
Non si rappresenta l’energia
dissipata
nelle
deformazioni
sostanzialmente elastiche del
sistema composto (generalmente
si assume uno smorzamento
viscoso pari al 5%)
F
F
Fy sistema
Controvento
elastico
Fy telaio
Telaio
KH sistema
O
dy telaio
d
d
CONTROVENTI ELASTICI
Comportamento ciclico del sistema composto telaio+controvento per telaio che
Sistema
entra IN CAMPO PLASTICO
Telaio+controvento
F
Nota bene:
Si considera trascurabile l’energia
dissipata dal controvento elastico
rispetto all’energia dissipata dal telaio.
Fy sistema
Controvento
elastico
Fy telaio
Telaio
KH sistema
O
dy telaio
d
Energia dissipata nel telaio
F
d
CONTROVENTI ELASTICI
Determinazione della rigidezza del controvento elastico
La rigidezza del telaio diminuisce all’aumentare della dimensione A del controvento, avendo posto
l’area del controvento
Ab
l’area del controvento di diametro φ5 cm
Abφ5
A= Ab / Abφ5
7
10
Rigidezza [kN/m]
6
10
5
10
4
10
Rigidezza del sistema
3
Rigidezza del telaio
10
Rigidezza del cv
2
10 -2
10
10
-1
10
0
10
1
2
10 A
CONTROVENTI DISSIPATIVI
Equivalenza tra il telaio ad 1 grado di libertà con CONTROVENTO DISSIPATIVO e
l’oscillatore elementare.
TELAIO AD 1 GRADO DI LIBERTÀ CON
CONTROVENTO DISSIPATIVO
OSCILLATORE ELEMENTARE
CONTROVENTI DISSIPATIVI
Comportamento statico incrementale del sistema telaio+controvento
d
F
F
Sistema
Telaio+controvento
Fy sistema
Fy telaio
Telaio
Controvento
dissipativo
Fy dissipatore
KH sistema
O
dy dissipatore
dy telaio
d
CONTROVENTI DISSIPATIVI
Comportamento ciclico del sistema composto telaio+controvento per telaio che
rimane IN CAMPO ELASTICO
F
Nota bene:
Sistema
Telaio+controvento
Si considera trascurabile l’energia
dissipata dal telaio rispetto all’energia
dissipata dal controvento dissipativo.
Telaio
Controvento
dissipativo
O
d
Energia dissipata nel dissipatore
F
d
CONTROVENTI DISSIPATIVI
Comportamento ciclico del sistema composto telaio+controvento per telaio che
entra IN CAMPO PLASTICO
F
Sistema
Telaio+controvento
Telaio
Controvento
dissipativo
Energia dissipata nel telaio
O
d
Energia dissipata nel dissipatore
F
d
dissipativi
COMPORTAMENTOControventi
ELASTO-VISCOSO
EQUIVALENTE
Esistono diversi metodi per individuare i parametri di un sistema elastico equivalente a
quello non lineare di partenza.
D. IWAN (1979) - classificazione riguardo al tipo di forzante
impiegata nell’analisi strutturale:
METODI BASATI SULLA
RISPOSTA ARMONICA
METODI BASATI SULLA
RISPOSTA ALEATORIA
•Harmonic Equivalent Linearizzation
(HEL)
•Stationary Random Equivalent
Linearizzation (SREL)
•Resonant Amplitude Matching (RAM)
•Average Period and Damping (APD)
•Dynamic Mass (DM)
•Average Stiffness and Energy (ASE)
•Constant Critical Damping (CCD)
•Geometric Stiffness (GS)
•Geometric Energy (GE)
COMPORTAMENTO ELASTO-VISCOSO EQUIVALENTE
Geometric Stiffness (GS + CCD)
I parametri del sistema elastico equivalente vengono determinati direttamente
dal ciclo di isteresi del sistema Telaio+CV
dissipativo
F
K eq = K t + K f ,cv = F d max
K f ,cv
(Rigidezza secante del CV dissipativo)
Kt
(Rigidezza elastica del telaio)
F
(Risposta massima del sistema)
d max
(Spostamento massimo del sistema)
Sistema
Telaio+controvento
Telaio
Ed
1 Ed
1
ζ eq =
=
2
4π E p 2π Keq ⋅ dmax
Ed
Ep =
(area del ciclo di isteresi del sistema)
1
2
K eq ⋅ d max
2
(Energia potenziale elastica
massima del sistema)
Controvento
dissipativo
O
d
COMPORTAMENTO ELASTO-VISCOSO EQUIV.TE (GS + CCD)
F
Sistema
Telaio+controvento
Comportamento elastico equivalente
Energia dissipata per viscosità
Telaio
Controvento
dissipativo
Rigidezza equivalente
F
keq =
d
O
d max
Smorzamento equivalente
ζ eq =
1 Ed
4π E p
Ed è l’energia dissipata nel ciclo
Ep è l’energia di deformazione in corrispondenza di dmax
d
Energia dissipata per isteresi
nel dissipatore
F
d
Controventi dissipativi EQUIV.TE (GS + CCD)
COMPORTAMENTO ELASTO-VISCOSO
F
Sistema
Telaio+controvento
Comportamento elastico equivalente
Energia dissipata per viscosità
Telaio
Controvento
dissipativo
Rigidezza equivalente
F
keq =
d
O
d max
Smorzamento equivalente
ζ eq =
1 Ed
4π E p
Ed è l’energia dissipata nel ciclo
Ep è l’energia di deformazione in corrispondenza di dmax
d
Energia dissipata per isteresi
nel telaio e nel dissipatore
F
d
COMPORTAMENTO ELASTO-VISCOSO EQUIV.TE (ASE)
Average Stiffness and Energy (ASE)
Il sistema elastico equivalente viene definito in termini di valori medi dei
parametri assunti come fondamentali: rigidezza ed energia
dissipata
K eq
K eq (d max
∫
)=
Ed ,eq (d max
d max
0
K ( x )dx
d max
∫
)=
d max
0
Ciclo elasto-viscoso
equivalente
F
y
E ( x )dx
d max
O
dy
dmax
K (x)
Ciclo di isteresi del
sistema
telaio+CV dissipativi
COMPORTAMENTO ELASTO-VISCOSO EQUIV.TE (ASE)
F
F
d
Sistema
Telaio+controvento
Comportamento elastico equivalente
Energia dissipata per viscosità equivalente
Telaio
Controvento
dissipativo
Energia dissipata per isteresi
nel dissipatore
O
d
Rigidezza equivalente (Metodo ASE)
⎡1 − α
(1 + ln µ ) + α ⎤⎥
keq = k1 ⎢
⎣ µ
⎦
k1 è la rigidezza di primo ramo
ζ0 è lo smorzamento viscoso
α è il fattore d’incrudimento
µ è la duttilità
Smorzamento equivalente (Metodo ASE)
⎡
⎛
1⎞ 2
⎤
πζ 0 ⎢(1 − α )⎜ µ 2 − ⎟ + αµ 3 ⎥ + 2(1 − α )(µ −1)2
3⎠ 3
⎛ 3 ⎞
⎝
⎣
⎦
⎟
ζ eq = ⎜⎜
2 ⎟
(1 − α )(1 + ln µ ) + αµ
⎝ 2πµ ⎠
COMPORTAMENTO ELASTO-VISCOSO EQUIV.TE (ASE)
F
F
d
Sistema
Telaio+controvento
Comportamento elastico equivalente
Energia dissipata per viscosità equivalente
Telaio
Controvento
dissipativo
Energia dissipata per isteresi
nel telaio e nel dissipatore
O
d
Rigidezza equivalente (Metodo ASE)
Ed è l’energia dissipata
dmax è lo spostamento massimo
ksec è la rigidezza secante
keq =
1
dmax
d max
∫ k (x)dx
sec
0
Smorzamento equivalente (Metodo ASE)
d max
Ed (x)dx
dmax ∫0
ζ eq =
2
2πkeq (dmax )dmax
3
APPLICAZIONI
La tecnica di protezione passiva delle strutture mediante dissipazione non è ancora
matura dal punto di vista del numero di applicazioni.
Fino al 2002, nel Nord-America i dissipatori sono stati installati all’incirca in 103
edifici e in molti ponti, sia per interventi di adeguamento che per nuove costruzioni
(Soong, Spencer, 2002).
ANDAMENTO DELL’IMPIEGO DI DISPOSITIVI DI DISSIPAZIONE
NELL’INGEGNERIA ANTISISMICA NEL NORD-AMERICA
APPLICAZIONI
SCUOLA DOMIZIANO VIOLA
Potenza (Progettazione 1990, Realizzazione 2003)
Adeguamento antisismico con controventi collegati alla struttura mediante
coprigiunti dissipativi.
LE APPLICAZIONI
SCUOLA DOMIZIANO VIOLA
Potenza (Progettazione 1990, Realizzazione 2003)
APPLICAZIONI
SCUOLA DOMIZIANO VIOLA
Potenza (Progettazione 1990, Realizzazione 2003)
Controventi Dissipativi
Particolare del coprigiunto dissipativo
APPLICAZIONI
SCUOLA MEDIA GENTILE - FERMI
Fabriano (Progettata 1990, Realizzata 1992)
Adeguamento antisismico mediante controventi dissipativi visco-elastici.
APPLICAZIONI
SCUOLA MEDIA GENTILE - FERMI
Fabriano (Progettata 1990, Realizzata 1992)
Adeguamento antisismico mediante controventi dissipativi visco-elastici.
Particolare del dissipatore
Particolare del collegamento
struttura-controvento
APPLICAZIONI
SCUOLA MEDIA BUSCIOLANO VIA LAZIO
Potenza (Progettazione …?, Realizzazione 2006)
APPLICAZIONI
SCUOLA MEDIA BUSCIOLANO VIA LAZIO
Potenza (Progettazione …?, Realizzazione 2006)
APPLICAZIONI
PALESTRA VIA ROMA
Potenza (Progettazione …?, Realizzazione 2006)
APPLICAZIONI
PALESTRA VIA ROMA
Potenza (Progettazione …?, Realizzazione 2006)
Protezione sismica della Torre Major a Città del Messico
Los Angeles City Hall
Pacific North West Baseball Stadium
Pacific Bell North – Sacramento (CA)
Marin County Hall of Justice
•
•
•
•
•
Building A and Building B, built
in the 1980’s, are two-story,
steel-framed structures with 230foot by 400-foot rectangular
footprints.
The roof of each building is a
metal deck supported on openweb steel joist framing that spans
to the wide flange columns.
The 2nd floor is concrete fill on
metal deck supported on 9-foot
deep steel truss joists and girders.
The bottom chord of the steel
trusses support the floor framing
for an interstitial space below the
2nd floor.
The original lateral-force
resisting systems of the buildings
utilized steel concentrically
braced frames located at the east
and west ends of the buildings.
Bay Area Office Buildings












