CORSO DI LAUREA IN INGEGNERIA ED-ARCH AA 2010/11
PROVA SCRITTA DI FISICA GENERALE DEL 10/gen/2012 VII°APPELLO
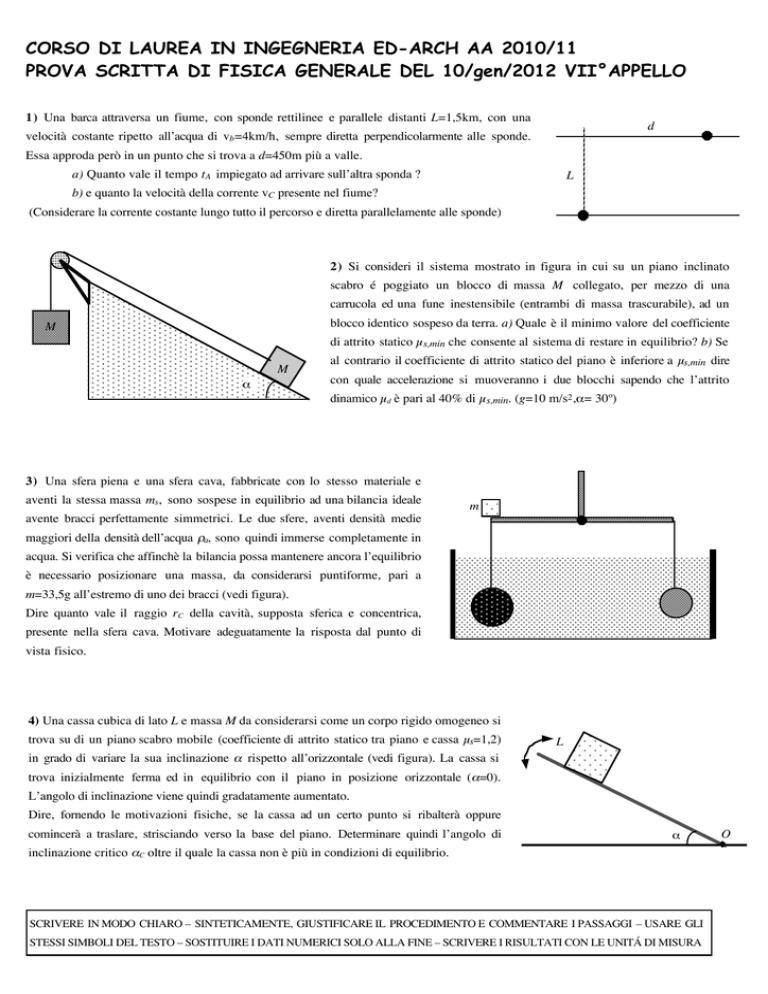
1) Una barca attraversa un fiume, con sponde rettilinee e parallele distanti L=1,5km, con una
d
velocità costante ripetto all’acqua di vb =4km/h, sempre diretta perpendicolarmente alle sponde.
Essa approda però in un punto che si trova a d=450m più a valle.
a) Quanto vale il tempo tA impiegato ad arrivare sull’altra sponda ?
L
b) e quanto la velocità della corrente vC presente nel fiume?
(Considerare la corrente costante lungo tutto il percorso e diretta parallelamente alle sponde)
2) Si consideri il sistema mostrato in figura in cui su un piano inclinato
scabro é poggiato un blocco di massa M collegato, per mezzo di una
carrucola ed una fune inestensibile (entrambi di massa trascurabile), ad un
blocco identico sospeso da terra. a) Quale è il minimo valore del coefficiente
M
di attrito statico µs,min che consente al sistema di restare in equilibrio? b) Se
M
α
al contrario il coefficiente di attrito statico del piano è inferiore a µs,min dire
con quale accelerazione si muoveranno i due blocchi sapendo che l’attrito
dinamico µd è pari al 40% di µs,min. (g=10 m/s2 ,α= 30º)
3) Una sfera piena e una sfera cava, fabbricate con lo stesso materiale e
aventi la stessa massa ms, sono sospese in equilibrio ad una bilancia ideale
m
avente bracci perfettamente simmetrici. Le due sfere, aventi densità medie
maggiori della densità dell’acqua ρa, sono quindi immerse completamente in
acqua. Si verifica che affinchè la bilancia possa mantenere ancora l’equilibrio
è necessario posizionare una massa, da considerarsi puntiforme, pari a
m=33,5g all’estremo di uno dei bracci (vedi figura).
Dire quanto vale il raggio rC della cavità, supposta sferica e concentrica,
presente nella sfera cava. Motivare adeguatamente la risposta dal punto di
vista fisico.
4) Una cassa cubica di lato L e massa M da considerarsi come un corpo rigido omogeneo si
trova su di un piano scabro mobile (coefficiente di attrito statico tra piano e cassa µs=1,2)
L
in grado di variare la sua inclinazione α rispetto all’orizzontale (vedi figura). La cassa si
trova inizialmente ferma ed in equilibrio con il piano in posizione orizzontale (α=0).
L’angolo di inclinazione viene quindi gradatamente aumentato.
Dire, fornendo le motivazioni fisiche, se la cassa ad un certo punto si ribalterà oppure
comincerà a traslare, strisciando verso la base del piano. Determinare quindi l’angolo di
α
inclinazione critico αC oltre il quale la cassa non è più in condizioni di equilibrio.
SCRIVERE IN MODO CHIARO – SINTETICAMENTE, GIUSTIFICARE IL PROCEDIMENTO E COMMENTARE I PASSAGGI – USARE GLI
STESSI SIMBOLI DEL TESTO – SOSTITUIRE I DATI NUMERICI SOLO ALLA FINE – SCRIVERE I RISULTATI CON LE UNITÁ DI MISURA
O
€
CORSO DI LAUREA IN INGEGNERIA ED-ARCH AA 2010/11
SOLUZIONI DELLA PROVA SCRITTA DI FISICA GENERALE DEL 10/Gen/2012
1) a) Il problema può essere risolto utilizzando lo schema dei moti relativi, in cui vb è il modulo del vettore velocità della barca nel
sistema di riferimento relativo (alla superficie dell’acqua) mentre vC è il modulo del vettore velocità di trascinamento. Si ha pertanto
r
r
r
per la relazione vettoriale:
vA = vC + v b = vC ιˆ + vb ˆj
r
dove vA è il vettore velocità nel sistema di riferimento assoluto (le sponde del fiume).
Il tempo di approdo tA sulla sponda opposta può essere ricavato dalla condizione:
€
L
3
vA,y tA = L
⇒
tA =
= h = 22, 5'
vb 8
b) La velocità della corrente può essere ricavata dalla condizione:
€vA,x tA = d
⇒
vC =
d
8
= 0, 45 km / h = 1,2km / h
tA
3
€
2) a) Le condizioni per l’equilibrio del sistema sono:
r r
Mg +T ' = 0 blocco sospeso
r r
r r
Mg +T '' + N + A s = 0
blocco sul piano scabro
r
T'
In base alle caratteristiche fisiche delle forze in gioco si ricavano da queste
equazioni€le seguenti relazioni scalari:
r
T ''
€
Mg −T = 0
⇒
T = Mg
−Mg sin α + T − As,max ≤ 0
se T > Mg sin α
−Mg sin α + T + As,max ≥ 0
−Mg cos α + N = 0
se T < Mg sin α
⇒
€
T = Mg > Mg sin α
e
As,max = µ sN = µ sMg cos α
si ottiene:
−Mg sin α + Mg − µs Mg cos α ≤ 0
µs€≥
1− sinα
cos α
⇒
µs,min =
1− sinα
3
=
= 0,577
cosα
3
b) Le equazioni della dinamica del sistema sono:
€
r r
r
Mg +T ' = M a' blocco sospeso
r r
r r
r
Mg +T '' + N + A d = M a' '
blocco sul piano scabro
Da queste si ricava, tenendo conto che l’accelerazione verticale del blocco sospeso
coincide in modulo con quella del blocco lungo il piano inclinato:
€
Mg −T = M a
−Mg sin α + T − µ d Mg cos α = M a
eliminando la tensione si ottiene:
€ − Mg sinα − µ Mg cos α = 2M a
Mg
d
a=
€
€
N = Mg cos α
essendo in questo caso sempre:
€
r
Mg
e quindi
g
g
1− sinα − 0, 4µ s,min cos α) = cos α µs,min (1− 0, 4) = 1,5m / s2
(
2
2
α
€
€
€
r
N
r
As
r
Mg
3) Dall’equilibrio dei momenti (polo nel fulcro della bilancia) si ricava:
( m + m s )g − ρ aVsc g =
m sg − ρ aVsp g
dove con Vsc e Vs p si è indicato rispettivamente il volume esterno della sfera cava e della sfera piena. Essendo costituite della stessa
sostanza la differenza
€ dei volumi esterni delle sfere coincide con il volume VC della cavità interna. Si ha pertanto dalla precedente
relazione:
m − ρ a Vsc = − ρ aVsp
⇒
(
)
m = ρ a Vsc − Vsp = ρ a VC
si ottiene infine:
€VC =
4
m
π rC3 =
3
ρa
⇒
rC = 3
3 m
= 2cm
4 π ρa
4) Occorre stabilire quale tra i due possibili moti si verificherà per primo all’aumentare
dell’angolo di inclinazione del piano.
€
Nel caso di moto strisciamento la cassa può essere schematizzata come un punto
materiale che si muove su di un piano scabro. Dalla teoria del moto di strisciamento è
noto che esiste un angolo critico di inclinazione oltre il quale un corpo poggiato su di
un piano inclinato scabro inizia a traslare. In questo caso: α c = arctan µ s = 50,2°
Il ribaltamento della cassa può avvenire solo se essa ruota facendo perno sullo spigolo S
€ crtitco corrisponde alla situazione
senza strisciare (vedi figura). In questo caso l’angolo
r
As
nella quale la cassa raggiunge un punto di equilibrio particolare in cui tutta la reazione
normale del piano è concentrata sullo spigolo e contemporaneamente il momento della
forza peso con polo sullo spigolo si annulla. Questo è possibile quando variando α la
r
Mg
€
La cassa pertanto si ribalterà senza strisciare una volta raggiunta l’inclinazione
€
α =45°.
max
Questa argomentazione fisica può essere resa in forma più rigorosa scrivendo le
relazioni d’equilibrio del corpo (I e II eq cardinale):
r
r r r
FRex = Mg + N + As = 0
r
r
r r
M Rex,S = S B × Mg + bN × N = 0
polo in S
Da queste relazione è possibile ricavare le seguenti relazioni scalari:
Mg cos€α − N = 0
Mgsinα − As = 0
N = Mg cos α
As = Mg sin α
⇒
⇒
π
2
L sin − α Mg − bN N = 0
2
4
⇒
π
2
L sin − α Mg − bN Mg cos α = 0
2
4
Dall’ultima relazione è possibile ricavare il punto di applicazione della reazione normale
indicato in figura con ΩN . Il braccio bN rappresenta infatti la distanza tra il polo e ΩN .
bN =
π
1
2
L sin − α
2
4
cosα
Per α=45° il braccio si annulla indicando che la reazione si trova applicata su S. Per
valori maggiori tale relazione non è più valida in quanto il braccio diviene negativo. Per
α>45° la reazione €
si trova in effetti sempre applicata in S e l’equilibrio non è più
possibile in quanto il momento della forza peso è diverso da zero e non ha più un
momento antagonista. Quindi la cassa ruota ribaltandosi.
B
Ω€
N
retta d’azione della forza peso passa sullo spigolo. Dalla geometria del corpo si ricava €
α c = 45°
che ciò è possibile quando l’angolo di inclinazione vale:
€
r
N
S
α
O
CORSO DI LAUREA IN INGEGNERIA ED-ARCH AA 2010/11
PROVA SCRITTA DI FISICA GENERALE DEL 10/Gen/2012 VII°APPELLO
DOMANDE DI TEORIA
Rispondere alle seguenti domande (verrà valutata l'esattezza, la chiarezza, la completezza e la sintesi delle risposte). Le risposte debbono
essere redatte esclusivamente sul foglio fornito dal docente che assiste alla prova debitamente compilato con nome, cognome e numero di
matricola dello studente. L'uso corretto e la scrittura dei simboli utilizzati sarà oggetto di valutazione. Si raccomanda inoltre di scrivere in
modo ordinato e con calligrafia chiara e comprensibile. Elaborati non conformi alle indicazioni riportate saranno valutati negativamente.
1) a) Che differenza c'è tra pulsazione (indicata in genere con il simbolo Ω ) e la velocità angolare (indicata in genere con ω)? Riportare
alcuni esempi di moto in cui intervengono le due grandezze. b) Vi sono dei moti particolari in cui le due grandezze sono in effetti
coincidenti?
2) Ricavare analiticamente la funzione energia potenziale U della forza peso a partire dalla definizione generale dell'energia potenziale.
3) Enunciare il principio di Pascal e darne dimostrazione in base alla legge di Stevino. Descrivere l'applicazione del torchio idraulico.












