Momento Torcente

Momento Torcente
Prima di tutto dobbiamo definire che cosa è un momento vettoriale, in quanto possiamo definire
un momento solo per un vettore (in effetti non è sempre così, ma per la fisica che facciamo noi
considereremo solo i momenti vettoriali). Il momento di un generico vettore v è:
𝑴𝒐 = 𝒓 × 𝒗
Ovvero il prodotto vettoriale fra il vettore posizione r e il vettore generico.
Esistono diversi tipi di momento:




MOMENTO ANGOLARE: Ovvero il momento rispetto al vettore quantità di moto;
MOMENTO MECCANICO: Ovvero il momento rispetto ad una forza;
MOMENTO ELETTRICO
MOMENTO MAGNETICO
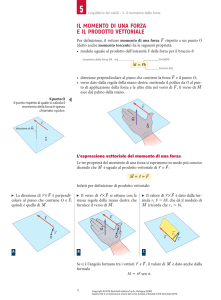
In particolare il momento meccanico di
una forza può essere rappresentato come
nel disegno accanto.
Notare come sia necessario, per calcolare
il modulo del momento, trovare il braccio
della forza b.
Il momento meccanico di una forza può
essere scomposto in due ulteriori
momenti: quello torcente e quello
flettente. Tuttavia, nelle nostre situazioni,
possiamo tranquillamente considerare il
momento meccanico come momento torcente. Un metodo molto semplice per vedere se una forza
esercita un momento torcente su un corpo è prevedere se il corpo stesso ruota.
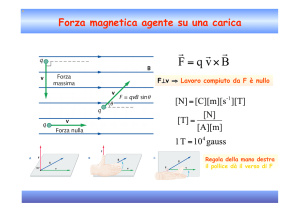
Un esempio è la chiave inglese con un bullone. Quando esercitiamo una forza
sulla chiave, creiamo anche un momento torcente che fa ruotare il bullone. Il
disegno accanto mostra una forza f che esercita un momento torcente T. E’
evidente che sotto tale forza il cilindro ruota in senso antiorario.
Ora, poiché i momenti sono dei vettori, può capitare che nonostante siano
applicate al corpo più forze, non si presenti alcun momento. Per esempio, se
applichiamo al cilindro anche una forza parallela alla prima e applicata al punto
diametralmente opposto, i momenti sono uguali ma opposti e quindi si annullano. Il cilindro quindi
non ruota.
Esempio
Calcoliamo il momento torcente (τ) esercitato dalla forza F (50 N) con r pari a 0.5 m e θ pari a 30°
(figura nella pagina successiva).
Sappiamo che:
𝐹𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑜𝑙𝑎𝑟𝑒 = 𝐹 sen 𝜃
𝐹𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑜𝑙𝑎𝑟𝑒 = 𝐹 sen 30°
𝐹𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑜𝑙𝑎𝑟𝑒 = 25 𝑁
E quindi il nostro momento torcente sarà:
𝜏 = 𝐹𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑜𝑙𝑎𝑟𝑒 ∙ 𝑟
𝜏 = 12.5 𝑁𝑚
Osserviamo come l’unità di misura del momento torcente sia Newton per Metro.