1995-1996 - Docenti.unina

Anno accademico 1995-1996
1) Siano 𝐶1 , 𝐶2 due circonferenze di centri e raggi rispettivi 𝑂1 , 𝑂2 e 𝑟1 , 𝑟2 . Dato
un punto 𝑃 esterno alle due circonferenze si considerino le tangenti per 𝑃 alle due
circonferenze e siano 𝑀1 , 𝑁1 e 𝑀2 , 𝑁2 i rispettivi punti di contatto. Si determini
il luogo dei punti tali che 𝑃𝑀12 + 𝑃𝑀22 = 1 .
Si discutano i punti 𝑃 per cui 𝑃𝑀12 + 𝑃𝑀22 è minima.
Prima di cominciare a risolvere l’esercizio proposto, è opportuno ripetere il
Teorema della mediana, un teorema di Geometria derivato dalla legge del coseno
o teorema di Lazare Carnot.
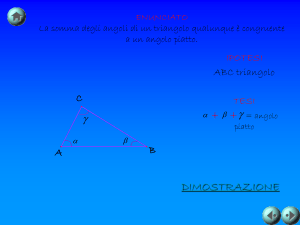
In altri termini, con riferimento al generico triangolo mostrato nella figura
precedente, vale l’identità
1
2𝑂𝑀 2 = 𝑂𝐴 2 + 𝑂𝐵 2 − 𝐴𝐵 2 ,
2
dove 𝑀 è il punto medio di 𝐴𝐵. Introdotti, infatti, i vettori
2
𝑎⃗ = 𝐴 − 𝑂 , 𝑏⃗⃗ = 𝐵 − 𝑂 , 𝑚
⃗⃗⃗ = 𝑀 − 𝑂 , 𝑢
⃗⃗ = 𝐵 − 𝑀 = 𝑀 − 𝐴 ,
si può scrivere
𝑎⃗ = 𝑚
⃗⃗⃗ − 𝑢
⃗⃗ , 𝑏⃗⃗ = 𝑚
⃗⃗⃗ + 𝑢
⃗⃗ .
Dunque, risulta
𝑎⃗ ∙ 𝑎⃗ = 𝑎2 = 𝑚2 + 𝑢2 − 2𝑚
⃗⃗⃗ ∙ 𝑢
⃗⃗ , 𝑏⃗⃗ ∙ 𝑏⃗⃗ = 𝑏 2 = 𝑚2 + 𝑢2 + 2𝑚
⃗⃗⃗ ∙ 𝑢
⃗⃗ .
Sommando membro a membro le due ultime relazioni, si elimina il prodotto
scalare 𝑚
⃗⃗⃗ ∙ 𝑢
⃗⃗ e si ottiene
𝑎2 + 𝑏 2 = 2𝑚2 + 2𝑢2 ,
da cui discende la tesi
1
2𝑚2 = 𝑎2 + 𝑏 2 − (2𝑢)2 .
2
Pertanto, in un triangolo qualsiasi il doppio del quadrato della mediana relativa
ad un lato è uguale alla somma dei quadrati degli altri due lati diminuito della
metà del quadrato del primo lato.
Venendo al problema proposto, si parta dall’osservazione attenta della figura che
segue, nella quale, volendo rappresentare il problema, si è considerato un
generico punto 𝑃 del piano, esterno alle due circonferenze, sono state tracciate le
quattro tangenti ad entrambe. Inoltre, per brevità di notazione, si introducono le
distanze del punto 𝑃 dai centri delle circonferenze
3
𝑑1 = 𝑃𝑂1 = √𝑃𝑀12 + 𝑟12 , 𝑑2 = 𝑃𝑂2 = √𝑃𝑀22 + 𝑟22 .
Ebbene, l’equazione del luogo assegnato
𝑃𝑀12 + 𝑃𝑀22 = 1
si può scrivere nella forma equivalente
𝑑12 + 𝑑22 = 1 + 𝑟12 + 𝑟22 .
Detto allora 𝑄 il punto medio del segmento 𝑎 = 𝑂1 𝑂2 , in forza del Teorema della
mediana applicato al triangolo 𝑂1 𝑃𝑂2 , si ottiene
4
1
1
2𝑃𝑄 2 = 𝑑12 + 𝑑22 − 𝑎2 = 1 + 𝑟12 + 𝑟22 − 𝑎2 .
2
2
Questa ultima relazione prova inequivocabilmente che il luogo descritto dai punti
𝑃 è una circonferenza. Precisamente, quando esiste, si tratta della porzione di
circonferenza, che ha il centro nel punto 𝑄 e di raggio
1
𝑟 = √2(1 + 𝑟12 + 𝑟22 ) − 𝑎2 ,
2
esterna sia a 𝐶1 che a 𝐶2 , dato che, quando il punto 𝑃 si trova all’interno di una di
esse, non è possibile tracciare la tangente.
Infine, la distanza 𝑃𝑀12 + 𝑃𝑀22 è minima quando il punto 𝑃 coincide con 𝑄, il punto
medio del segmento 𝑂1 𝑂2 , sicché
𝑎2
= 1 + 𝑟12 + 𝑟22 → 𝑟 = 0
2
ed il luogo degenera nel solo punto 𝑄.
5
2) Dati quattro punti distinti nel piano dimostrare che è sempre possibile
sceglierne tre che determinino un angolo inferiore o uguale a 45°. In generale dati
𝑛 punti dimostrare che se ne possono scegliere 3 che determinino un angolo
inferiore o uguale a 180°/𝑛.
Prima di discutere la soluzione, è conveniente sottolineare che in quel che segue
nessuna terna di punti considerati è da ritenersi allineata; se così non fosse, si
avrebbe una soluzione banale.
Caso particolare 𝑛 = 4
Si comincia con il caso dei quattro punti. Se l’angolo in 𝑃 è ottuso, allora nel
triangolo 𝐴𝑃𝐵 il più piccolo fra gli angoli in 𝐴 o in 𝐵 deve essere minore di 45°,
perché la somma degli angoli in 𝐴, in 𝐵 e in 𝑃 vale 180°. Se viceversa tale angolo è
retto o acuto, allora la retta congiungente 𝑃 con il quarto vertice 𝐶 divide l’angolo
in due parti, una almeno delle quali deve essere minore o uguale a 45°.
Caso generale
Il problema chiede di dimostrare che è sempre possibile, dati 𝑛 punti nel piano
(𝑛 ≥ 3), trovare un angolo convesso che ha vertice in uno di essi, lati che passano
per altri due punti, e che contiene i restanti 𝑛 − 3 punti: basta prendere
6
l’involucro convesso degli 𝑛 punti, scegliere un vertice 𝑃 del poligono delimitante
l’involucro e le due semirette che escono da 𝑃 e passano per i due vertici adiacenti
𝐴 e 𝐵.
Nel caso generale si procede in modo simile. Scelto un angolo 𝐴𝑃𝐵 che contiene i
restanti punti all’interno si hanno due casi: o tale angolo supera (1 − 2/𝑛) 180°, e
allora nel triangolo 𝐴𝑃𝐵 uno degli angoli in 𝐴 o in 𝐵 deve essere minore di 180°/𝑛,
oppure, in caso contrario, le rette che congiungono 𝑃 con i restanti 𝑛 − 3 punti
dividono l’angolo in 𝑃 in 𝑛 − 2 angoli che, se fossero tutti maggiori di 180°/𝑛
darebbero per l’angolo in 𝑃 una ampiezza più grande di (1 − 2/𝑛) 180°, contro
l’ipotesi.
Si noti che il risultato non è migliorabile: nel caso del poligono regolare di 𝑛 lati
gli angoli formati da due diagonali consecutive uscenti dallo stesso vertice
valgono esattamente 180°/𝑛.
7
3) Dimostrare che, se 𝑎, 𝑏, 𝑐 sono interi consecutivi, allora 𝑎3 + 𝑏 3 + 𝑐 3 è multiplo
di 9.
Se si pone
𝑎 = 𝑛 − 1 , 𝑏 = 𝑛 , 𝑐 = 𝑛 + 1 , con 𝑛 ∈ ℕ ,
risulta indubbiamente
𝑎3 + 𝑏 3 + 𝑐 3 = (𝑛 − 1)3 + 𝑛3 + (𝑛 + 1)3 = 3(𝑛3 + 2𝑛)
e, quindi, basta dimostrare che la successione di interi
𝑎𝑛 = 𝑛3 + 2𝑛
è dividibile per 3. La successione è dispari, nel senso che 𝑎0 = 0 e
𝑎−𝑛 = −𝑎𝑛 , con 𝑛 ≥ 1 .
Pertanto, si restringerà l’attenzione soltanto ai valori positivi dell’indice e si
procederà per induzione. I primi termini della successione, come mostra la tabella
che segue, sono tutti divisibili per 3.
𝑛
1
2
3
2
𝑎𝑛
3
12
33
72
Se poi, per ipotesi, si suppone che 𝑎𝑛 sia divisibile per tre, allora anche 𝑎𝑛+1 deve
esserlo. Simbolicamente, si ha
8
𝑎𝑛 = 3𝐻 → 𝑎𝑛+1 = 3𝐾 ( 𝐻, 𝐾 interi) .
Infatti, si può scrivere
𝑎𝑛+1 = (𝑛 + 1)3 + 2(𝑛 + 1) = 𝑛3 + 3𝑛2 + 5𝑛 + 3 = 𝑎𝑛 + 3(𝑛2 + 𝑛 + 1) .
Ora, ponendo 𝑎𝑛 = 3𝐻, la relazione precedente diventa
𝑎𝑛+1 = 3𝐻 + 3(𝑛2 + 𝑛 + 1) ,
da cui si evince elementarmente che anche 𝑎𝑛+1 è divisibile per tre. Resta in tal
modo dimostrato che il cubo di tre interi consecutivi è un multiplo di tre.
Una maniera di procedere più breve e raffinata, ma un tantino più complicata, è la
seguente. Dato che si può scrivere
(𝑛 − 1)𝑛(𝑛 + 1) + 9𝑛 ,
𝑎3 + 𝑏 3 + 𝑐 3 = (𝑛 − 1)3 + 𝑛3 + (𝑛 + 1)3 = 3 ⏟
sempre divsibile per 3
si conclude immediatamente la divisibilità per 9 per ogni valore di 𝑛.
9
4) Sia 𝑓 ∶ ℝ → ℝ una funzione non negativa, con concavità rivolta verso il basso,
derivabile e tale che 𝑓′(0) > 0 e 𝑓(𝑥) = 𝑓(2 − 𝑥) per ogni 𝑥 ∈ ℝ.
Dimostrare che
2
[𝑓(1) − 𝑓(0)]2
∫ 𝑓(𝑥) 𝑑𝑥 ≤ 2𝑓(1) −
.
𝑓′(0)
0
Provare che se la condizione 𝑓(𝑥) = 𝑓(2 − 𝑥) non è verificata, la diseguaglianza
(∗) può non valere.
Si comincia con il dimostrare che, stante l’ipotesi 𝑓(𝑥) = 𝑓(2 − 𝑥), l’intervallo di
integrazione può essere dimezzato, sicché
2
1
2
1
∫ 𝑓(𝑥) 𝑑𝑥 = ∫ 𝑓(𝑥) 𝑑𝑥 + ∫ 𝑓(2 − 𝑥) 𝑑𝑥 = 2 ∫ 𝑓(𝑥) 𝑑𝑥 .
0
0
1
0
𝑦
𝑦 = 𝑥𝑓′(0) + 𝑓(0)
𝑀
𝑓(1)
𝑓(0)
𝑂
𝐴
1
2
10
𝑥
Dunque, la relazione di simmetria assegnata impone una simmetria rispetto alla
retta verticale 𝑥 = 1. Inoltre, derivandola, si può scrivere
𝑓(𝑥) = 𝑓(2 − 𝑥) → 𝑓 ′ (𝑥) = −𝑓′(2 − 𝑥)
e dedurre che 𝑓′(1) = 0, sicché la funzione presenta in 𝑥 = 1 un massimo relativo.
Se si interseca la tangente nell’origine con la tangente passante per il massimo, si
ottiene il punto
{
𝑓(1) − 𝑓(0)
𝑦 = 𝑥𝑓′(0) + 𝑓(0) ,
→ 𝑥=
.
𝑦 = 𝑓(1) ,
𝑓′(0)
𝑦
𝑃
𝐶
𝑀
𝐵
𝑂
𝑥
𝐴
Segue allora che l’integrale definito tra zero ed uno si può maggiorare con la
differenza dell’area del rettangolo in grigio 𝑂𝐴𝑀𝐶 e del triangolo in rosso 𝐵𝐶𝑃, in
modo che sia
2
1
∫ 𝑓(𝑥) 𝑑𝑥 = 2 ∫ 𝑓(𝑥) 𝑑𝑥 = 2𝑓(1) − 2
0
0
11
𝑓(1) − 𝑓(0)
[𝑓(1) − 𝑓(0)] ,
2 𝑓′(0)
da cui segue la tesi desiderata.
Qualora la relazione di simmetria 𝑓(𝑥) = 𝑓(2 − 𝑥) non fosse verificata, come
accade per la parabola
𝑓(𝑥) = 1 + 4𝑥 − 𝑥 2 [𝑓(1) = 4 , 𝑓(0) = 1 , 𝑓′(0) = 4] ,
allora la maggiorazione non è più valida, essendo
2
2
∫ 𝑓(𝑥) 𝑑𝑥 = ∫ (4𝑥 − 𝑥
0
0
2)
[𝑓(1) − 𝑓(0)]2 23
22
𝑑𝑥 =
> 2𝑓(1) −
=
.
3
𝑓′(0)
4
12
5) Dato 𝐴 = {(𝑥, 𝑦) ∈ ℝ2 ∶ |𝑥|2𝑎 + |𝑦|2𝑎 ≤ 1} ove 𝑎 ∈ ℝ, 𝑎 > 0, si consideri
al variare di 𝑘 ≥ 0 la classe 𝐶 degli insiemi
𝐵𝑘 = {(𝑥, 𝑦) ∈ ℝ2 ∶ |𝑥| + |𝑦| ≤ 𝑘}
contenuti in 𝐴. Determinare 𝑘 in funzione di 𝑎 in modo che 𝐵𝑘 abbia area massima
tra gli insiemi di 𝐶.
Gli insiemi 𝐵𝑘 sono una famiglia di quadrati, tutti centrati nell’origine e con vertici
sugli assi; il lato del quadrato vale 𝐿 = 𝑘√2 e, pertanto, al crescere del parametro
i quadrati diventano sempre più grandi. Ad esempio, nella figura è rappresentato
il caso 𝑘 = 2. Scopo dell’esercizio è, fissato un valore di 𝑎, determinare il massimo
valore di 𝑘 per cui 𝐵𝑘 ⊆ 𝐴.
Inoltre, per 𝑎 = 1/2, risulta banalmente 𝐴 = 𝐵1 , per cui il massimo valore risulta
𝑘𝑀 = 1. Nella figura che segue sono mostrati gli insieme 𝐴 per tre valori possibili
di 𝑎, precisamente, procedendo da sinistra verso destra, si riportano i casi 𝑎 =
13
1/2 una quadrato, 𝑎 = 1 una circonferenza, 𝑎 = 2 un quadrato con gli angoli
smussati.
Appare evidente che per 𝑎 ≥ 1/2, il massimo quadrato contenuto è sempre 𝐵1 e,
pertanto, risulta sempre 𝑘𝑀 = 1. D’altra parte, algebricamente si può scrivere
|𝑥|2𝑎 + |𝑦|2𝑎 ≤ |𝑥| + |𝑦| ≤ 1 , per 𝑎 ≥
1
.
2
Per 0 < 𝑎 < 1/2, le cose sono un pochino più complicate, dato che le curve 𝐴
assumono un aspetto più complicato. Ad esempio, la figura che segue illustra il
caso 𝑎 = 1/10.
14
Limitandosi per semplicità al tratto di curva del primo quadrante, le due curve
𝑥 + 𝑦 = 𝑘𝑀 e 𝑥 2𝑎 + 𝑦 2𝑎 = 1
devono essere tangenti. Per la evidente simmetria in gioco, esse si toccheranno
lungo i punti della bisettrice 𝑦 = 𝑥, sicché il punto di tangenza vale
2𝑥 = 𝑘𝑀 , 2𝑥
2𝑎
𝑘𝑀 2𝑎
1
= 1 → 2 ( ) = 1 → 𝑘𝑀 = 21−1/(2𝑎) per 0 < 𝑎 < .
2
2
In definitiva, si può dire che la funzione cercata, rappresentata in figura, vale
21−1/(2𝑎)
0<𝑎<
1
𝑎≥
𝑘𝑀 (𝑎) = {
15
1
.
2
1
,
2
Si noti che questa funzione presenta due interessanti caratteristiche: presenta un
punto angoloso in 𝑎 = 1/2; tutte le derivate si annullano nel limite per 𝑎 → 0+ .
Le curve algebriche piane dovute a Gabriel Lamé (Tours, 22 luglio 1795 – Parigi, 1 maggio 1870)
si possono scrivere nella forma
𝑥 𝛼
𝑦 𝛼
( ) +( ) =1,
𝑎
𝑏
dove 𝛼 è un numero razionale, positivo o negativo, detto indice della curva. Sono esempi di
curve di Lamé la retta, l’ellisse, l’asteroide e l’iperbole, che si ottengono, rispettivamente, per
𝛼 = 1, 𝛼 = 2, 𝛼 = 2/3, 𝛼 = −1. Le curve di Lamé rappresentano una generalizzazione delle
coniche. Il nome Lamé è inciso sulla Torre Eiffel.
16
6) Siano 𝑎, 𝑏 numeri reali non negativi tali che 𝑏 2 + 𝑏 6 ≤ 𝑎2 − 𝑎6 . Dimostrare che
allora risulta:
1) 𝑎 ≤ 1 ,
2) 𝑏 < 2/3 .
Dato che i numeri reali in esame sono non negativi, deve essere
𝑎2 − 𝑎6 ≥ 0 → 𝑎2 (1 − 𝑎2 )(1 + 𝑎2 ) ≥ 0 → 0 ≤ 𝑎 ≤ 1
e così la prima implicazione è subito verificata.
La funzione
𝑓(𝑎) = 𝑎2 − 𝑎6 , con 0 ≤ 𝑎 ≤ 1 ,
è mostrata nella figura che segue e presenta un massimo relativo nel punto
17
𝑎𝑀 =
1
4
√3
, 𝑓(𝑎𝑀 ) =
1
√3
−
1
√27
=
2
3 √3
=𝑘,
dal momento che essa è strettamente crescente nell’intervallo
2𝑎 − 6𝑎5 > 0 → 3𝑎4 < 1 → 0 < 𝑎 <
1
4
√3
.
Per contro, per valori non negativi di 𝑏, si può scrivere
𝑏 2 + 𝑏 6 ≤ 𝑘 → 𝑏 6 ≤ 𝑘 − 𝑏 2 → 𝑘 − 𝑏 2 ≥ 0 → 0 ≤ 𝑏 ≤ √𝑘 <
Laddove l’ultima disuguaglianza è presto verificata, dato che
√𝑘 <
2
4
2
4
→ 𝑘<
→
<
→ 3 < 2√3 → 9 < 12 .
3
9
3 √3 9
18
2
,
3