La legge di Stefan Boltzmann

La legge di Stefan Boltzmann
Appunti per la realizzazione dell’esperienza di laboratorio
Premessa
Tutti i corpi caldi emettono energia in modo simile a un corpo nero. La legge di Stefan Boltzmann afferma
che la potenza totale irraggiata da un corpo per unità di superficie è proporzionale alla quarta potenza della
temperatura assoluta
𝑊
𝑆
= 𝐴𝜈,𝑇 𝜎𝑇 4
(1
dove σ=5,67∙10-8 Wm2K-4 è la costante di Stefan-Boltzmann e Aν,T≤1 è il potere assorbente del corpo. Un
piccolo foro praticato in una cavità, a causa delle numerose riflessioni interne, approssima al meglio il corpo
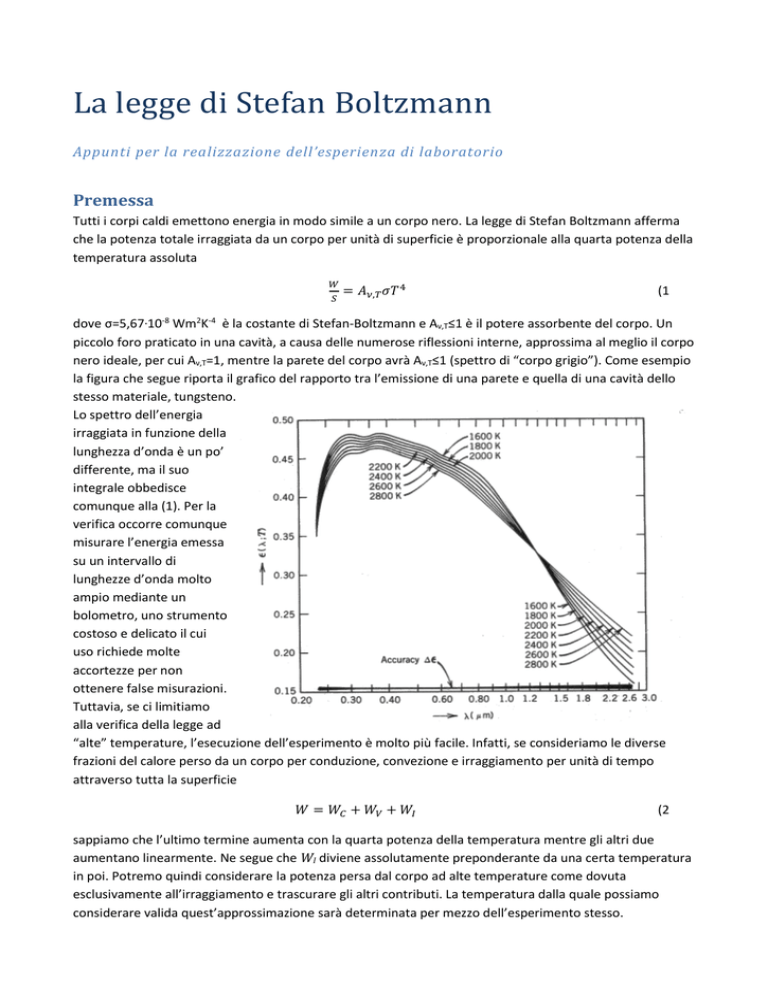
nero ideale, per cui Aν,T=1, mentre la parete del corpo avrà Aν,T≤1 (spettro di “corpo grigio”). Come esempio
la figura che segue riporta il grafico del rapporto tra l’emissione di una parete e quella di una cavità dello
stesso materiale, tungsteno.
Lo spettro dell’energia
irraggiata in funzione della
lunghezza d’onda è un po’
differente, ma il suo
integrale obbedisce
comunque alla (1). Per la
verifica occorre comunque
misurare l’energia emessa
su un intervallo di
lunghezze d’onda molto
ampio mediante un
bolometro, uno strumento
costoso e delicato il cui
uso richiede molte
accortezze per non
ottenere false misurazioni.
Tuttavia, se ci limitiamo
alla verifica della legge ad
“alte” temperature, l’esecuzione dell’esperimento è molto più facile. Infatti, se consideriamo le diverse
frazioni del calore perso da un corpo per conduzione, convezione e irraggiamento per unità di tempo
attraverso tutta la superficie
𝑊 = 𝑊𝐶 + 𝑊𝑉 + 𝑊𝐼
(2
sappiamo che l’ultimo termine aumenta con la quarta potenza della temperatura mentre gli altri due
aumentano linearmente. Ne segue che WI diviene assolutamente preponderante da una certa temperatura
in poi. Potremo quindi considerare la potenza persa dal corpo ad alte temperature come dovuta
esclusivamente all’irraggiamento e trascurare gli altri contributi. La temperatura dalla quale possiamo
considerare valida quest’approssimazione sarà determinata per mezzo dell’esperimento stesso.
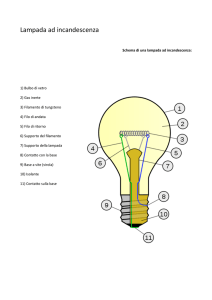
Per la verifica sperimentale si presta molto bene l’utilizzo di una comune lampadina a filamento di
tungsteno, materiale in grado sopportare temperature molto elevate. Inoltre la lampadina è progettata, al
fine di aumentare l’efficienza, per disperdere poco calore per conduzione (tramite i fili di contatto) o
convezione (il gas a bassa pressione nel bulbo) e massimizzare l’irraggiamento. Per un migliore risultato è
consigliabile l’uso di una lampadina alogena: l’utilizzo del gas alogeno diminuisce l’evaporazione del
tungsteno e consente di raggiungere temperature più elevate prima della distruzione della lampada. La
temperatura del filamento sarà ricavata dalla misura della sua resistenza elettrica, che è funzione della
temperatura.
Scopo della misura è ricavare la potenza fornita alla lampada in funzione della temperatura, che in
condizioni stazionarie è data dalla (2). Al di sopra di una certa temperatura possiamo trascurare i primi due
termini della (2) che diviene
𝑊 = Aν,T 𝜎𝑆𝑇 4 ,
(3
dove abbiamo trascurato l’energia irraggiata e riflessa dall’ambiente che colpisce il filamento e viene
assorbita. Prendendo il logaritmo naturale di entrambi i membri della (3)
𝐿𝑛(𝑊) = 𝐿𝑛(𝐴𝜈,𝑇 𝜎𝑆) + 4𝐿𝑛(𝑇)
(4
Il cui grafico in funzione di Ln(T) è una retta. Poiché in realtà la potenza misurata contiene tutti i termini
della (2) il grafico non sarà una retta. Tuttavia ci aspettiamo che da una certa temperatura in poi il grafico
assuma un andamento rettilineo: quello è il tratto in cui l’ultimo termine della (2) prevale sugli altri. La
pendenza della retta tracciata sui dati ad alta temperatura ci permetterà di ricavare l’esponente della legge
che ci siamo proposti di verificare.
L’apparato sperimentale
Il materiale occorrente per l’esperimento è il seguente:
1.
2.
3.
4.
5.
6.
L, Lampadina alogena 12V 10W con portalampada e relativo sostegno
RS, Resistenza a filo di precisione da 1,00 Ω (errore 0,1%) di alto wattaggio
A, Alimentatore regolabile in continua 30V 5A o superiore
VL e VR, due voltmetri
ρ(T), la relazione fra la resistività del tungsteno e la sua temperatura
Un termometro per misurare la temperatura ambiente
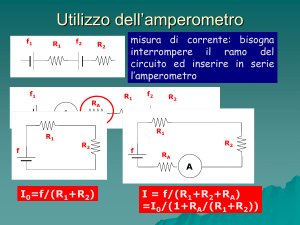
Si monta il circuito come in figura, con la
resistenza RS in serie alla lampada, il
voltmetro VL in parallelo alla lampada
(collegato quanto più possibile vicino a essa)
e il voltmetro VR in parallelo a RS .
+
-
L1
0.000
1
12V_10W
3
R1
Una nota pratica: occorre assolutamente
evitare di toccare la lampadina con le mani. Il
grasso delle impronte digitali sporca il vetro
che perde la sua trasparenza producendo
due effetti. Il primo è il surriscaldamento
della lampada e quindi la sua precoce
distruzione, che spesso impedisce di
1.0
V1
30 V
2
+
0.000
V
U1
DC 10M
V
VL
DC 10M
raggiungere le temperature più alte. Il secondo è la riflessione di parte dello spettro da parte del bulbo
sporco, che falsifica i risultati. Se ci si accorge di aver sporcato la lampada si può tentare di pulirla con alcool
e un fazzoletto di carta, tenendo presente che comunque rimarrà un alone che peggiorerà la prestazione
della lampada.
Svolgimento
Misurare la temperatura ambiente T0 con il termometro quindi alimentare il circuito e prendere le misure
nella seguente tabella:
VL±Δ VL (V)
VR±Δ VR (V)
I±ΔI (A)
R±ΔR (Ω)
R/R0±Δ(R/R0)
T±ΔT (K)
P±ΔP (W)
Ln(T/T0)±Er
Ln(P/P0)±Er
La resistenza elettrica del filamento a bassa temperatura è molto piccola, per cui non è consigliabile usare il
multimetro come Ohmmetro, perché si aggiungerebbe la resistenza dei cavi di collegamento. Invece è
consigliabile prendere qualche misura nella tabella con una corrente molto piccola (quanto piccola dipende
dalla sensibilità del voltmetro a disposizione) ad esempio 50mA (che corrispondono a 50mV sul voltmetro
VR) in modo che la corrente stessa non scaldi il filamento e questo rimanga effettivamente a temperatura
ambiente. La resistenza R(T0) si calcola poi con la legge di Ohm. Eseguendo la misura della resistenza in
questo modo non si aggiunge l’errore dovuto alla resistenza dei cavi del voltmetro (perché sui fili del
voltmetro VL scorre pochissima corrente a causa dell’alta impedenza del voltmetro e non c’è caduta di
tensione). La misura includerà i cavi e i contatti dal punto in cui è connesso il voltmetro: per questo è
importante che i contatti dei fili di VL siano il più possibile prossimi alla lampada.
Nelle ultime due colonne della tabella la scelta di calcolare le grandezze relative alla temperatura ambiente
è data dalla volontà di utilizzare grandezze adimensionali e non dipendenti dalla temperatura iniziale e da
altre caratteristiche peculiari della lampada utilizzata, ma non è una scelta obbligata.
Elaborazione dei dati sperimentali
Una volta raccolti i dati nelle prime due colonne della tabella è facile ricavare le grandezze derivate nelle
altre colonne, tranne che per la temperatura che richiede un discorso a parte. Sappiamo che la variazione
della resistenza elettrica, espressa per mezzo della seconda legge di Ohm è
𝑅(𝑇)
𝑅(𝑇0 )
𝜌(𝑇) 𝑙 𝑆0
0 0 𝑆
= 𝜌(𝑇 ) 𝑙
(5
Che include quindi anche la variazione dimensioni del conduttore dovute alla dilatazione termica. Detto
𝜆 = 5𝑥10−6 𝐾 −1 il coefficiente di dilatazione lineare del tungsteno,
𝑅(𝑇)
𝑅(𝑇0 )
𝜌(𝑇)
1
𝜌(𝑇)
1
1+𝜆Δ𝑇
0
= 𝜌(𝑇 ) (1 + 𝜆Δ𝑇) ⋅ (1+𝜆Δ𝑇)2 = 𝜌(𝑇 )
0
.
(6
Dato che l’intervallo di temperatura raggiunge al massimo i 2500 K, il prodotto T può essere al massimo
0.0125, con una differenza massima fra il rapporto della resistenza e quello della resistività dell’1,3% che
tralasciamo perché inferiore all’errore commesso dagli strumenti e per semplicità di calcolo.
La legge della variazione della resistività del tungsteno vale
𝑇 𝐵
𝑇0
𝜌(𝑇)
𝜌(𝑇0 )
=( )
𝑇=
𝜌(𝑇) 𝐵
𝑇0 [𝜌(𝑇 )]
0
(7
Dove B=1,165. Quindi
1
1
≅
𝑅(𝑇) 𝐵
𝑇0 [𝑅(𝑇 )] .
0
(8
Calcolo degli errori
Per completare la tabella e fare il grafico dobbiamo valutare gli errori. Per le misure prese direttamente
dobbiamo fare riferimento al manuale del voltmetro per individuare l’errore. Nel nostro caso VL è stata
letta con un multimetro da banco con errore 0,05% sulla scala da 100mV, errore 0,03% sulla scala da 1V,
errore 0,02% sulla scala da 10V, mentre VRS è stata letta con un multimetro di accuratezza 0,1%+2digit.
Per le grandezze derivate utilizziamo la propagazione degli errori (con ΔA si intende l’errore sulla grandezza
A):
Δ𝐼 Δ𝑅𝑆 Δ𝑉𝑅𝑠
=
+
𝐼
𝑅𝑆
𝑉𝑅𝑠
Δ𝑅 Δ𝑉𝐿 Δ𝐼 Δ𝑉𝐿 Δ𝑅𝑆 Δ𝑉𝑅𝑠
=
+
=
+
+
𝑅
𝑉𝐿
𝐼
𝑉𝐿
𝑅𝑆
𝑉𝑅𝑠
E analoga formula per R(T0), che è la prima misura della serie. Proseguendo
Δ𝑅𝑆
= 0,001
𝑅𝑆
𝑅(𝑇)
) Δ𝑅(𝑇) Δ𝑅(𝑇 )
𝑅(𝑇0 )
0
=
+
𝑅(𝑇)
𝑅(𝑇)
𝑅(𝑇0 )
(
)
𝑅(𝑇0 )
Δ(
1
Δ𝑇 Δ𝑇0
=
+
𝑇
𝑇0
𝑅(𝑇) 𝐵
Δ[
]
𝑅(𝑇0 )
1
𝑅(𝑇) 𝐵
[
]
𝑅(𝑇0 )
R(T)
Δ𝑇0 1 Δ (𝑅(𝑇0 )) Δ𝑇0 1 Δ𝑅(𝑇) Δ𝑅(𝑇0 )
=
+
=
+ (
+
)
𝑇0
𝐵 R(T)
𝑇0
𝐵 𝑅(𝑇)
𝑅(𝑇0 )
(
)
𝑅(𝑇0 )
Doev T0 è la misura eseguita con il termometro. Infine abbiamo
Δ𝑃 Δ𝑉𝐿 Δ𝐼 Δ𝑉𝐿 Δ𝑅𝑆 Δ𝑉𝑅𝑠
=
+
=
+
+
𝑃
𝑉𝐿
𝐼
𝑉𝐿
𝑅𝑆
𝑉𝑅𝑠
𝑃
Δ𝑃 Δ𝑃0
Δ [𝐿𝑛 ( )] =
+
𝑃0
𝑃
𝑃0
𝑇0
ΔT Δ𝑇0
Δ [𝐿𝑛 ( )] =
+
𝑇
𝑇
𝑇0
Con questi errori possiamo tracciare il grafico e ricavare la pendenza della retta con il relativo errore.
Ln(P/P0) vs Ln(T/T0)
011
011
011
011
y = 3.9913x + 1.7089
R² = 0.9983
011
010
010
010
010
010
009
002
002
002
002
002
002
003