mi preparo per la verifica

Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
MI PREPARO PER LA VERIFICA
MODULO 1
Convertitori A/D e D/A
1. Il segnale sinusoidale unipolare della figura 1 deve essere campionato ad una frequenza 4 volte
superiore alla sua, ed i valori ottenuti debbono essere scritti in un codice binario naturale a 4 bit
sapendo che il fondo scala è di 5,120 V.
Fig. 1
2. Un ADC unipolare ad 8 bit ha in uscita la parola 1000 0110. Considerando che la tensione di
riferimento è 5,120 V, determina il valore della corrispondente tensione d’ingresso.
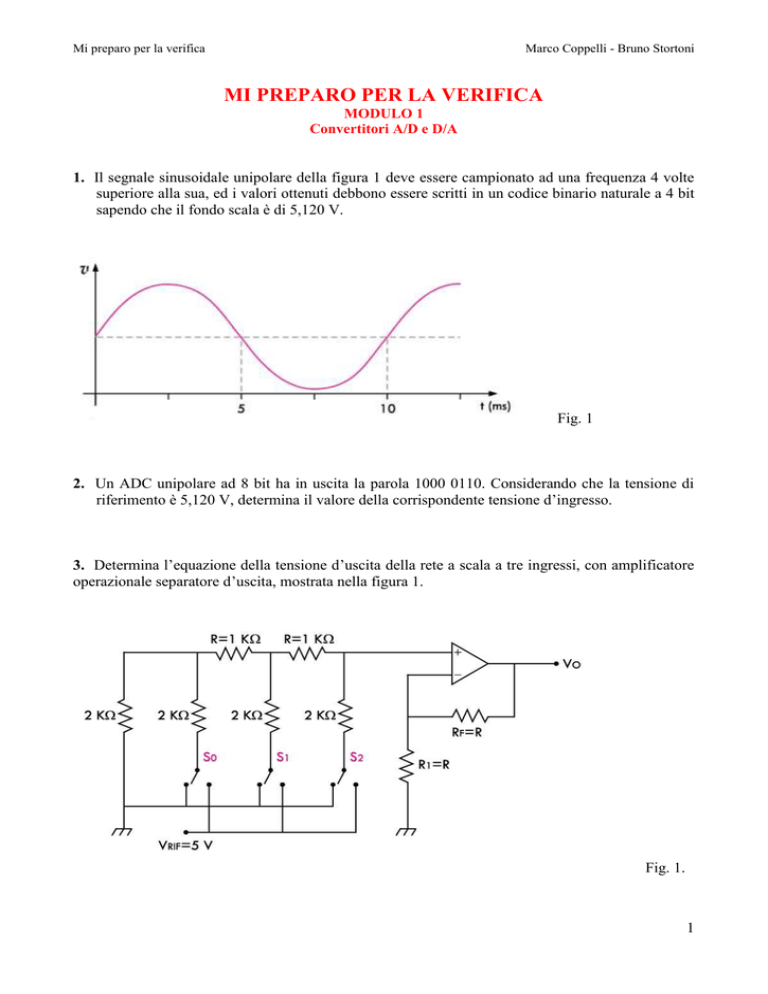
3. Determina l’equazione della tensione d’uscita della rete a scala a tre ingressi, con amplificatore
operazionale separatore d’uscita, mostrata nella figura 1.
Fig. 1.
1
Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
SOLUZIONI DEL
MI PREPARO PER LA VERIFICA
MODULO 1
Convertitori A/D e D/A
1. Dall’esame della figura notiamo che il periodo è di 10 ms e, poiché occorre campionare ad una
frequenza quattro volte superiore, il periodo di campionamento risulta:
10  10 3
Ts 
 2,5 ms.
4
Dato che lavoriamo a 4 bit, l’intera escursione della tensione sull’asse delle ordinate va divisa in 16
valori (quindici intervalli): da 0000 ad 1111. Ciascun valore differisce dal precedente per
l’ampiezza di un quanto Q. Il valore di Q è dato da:
Q
U RIF 5,120

 0,32 V
16
24
Graduiamo l’asse delle ascisse ogni 2,5 ms e quello delle ordinate ogni 0,32 V.
Sull’asse delle ordinate, a fianco di ciascun valore della tensione scriviamo il corrispondente valore
del codice: a 0 V corrisponde 0000, a 0,32 V corrisponde 0001, a 0,64 V corrisponde 0010 e così
via fino a 4,8 V (URIF ‒ Q) che corrisponde ad 1111.
Procediamo quindi a leggere i valori dell’ampiezza della tensione ogni 2,5 ms a partire dallo zero
assegnandogli il codice più vicino in modo che l’errore sia sempre inferiore a 1/2 Q = 1/2 LSB.
Otteniamo i seguenti valori:
Tempo (ms)
0
2,5
5
7,5
10
Codice
1000
1111
1000
0001
1000
2. La tensione d’ingresso può essere calcolata tramite la nota espressione che viene qui di seguito
riportata:
b
b
b 
b
U o  U RIF  n1  n 2  n 3  ...  on  V
4
8
2 
 2
2
Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
Per la parola ad 8 bit dell’esercizio, la precedente diventa:
0
1
1
0 
1 0 0 0
U o  5,120      



 = 5,120 · 0,5234375 = 2,68 V
 2 4 8 16 32 64 128 256 
Possiamo pervenire allo stesso risultato impiegando una delle tabelle contenute nei manuali delle
case costruttrici.
I quattro bit più significativi (1000) danno origine all’apporto maggiore della tensione (colonna
VMS GROUP):
1000  2,560 V
mentre i quattro bit meno significativi (0110) danno origine alla tensione letta nella colonna VLS
GROUP:
0110  0,120 V
Il risultato totale è dato dalla somma delle due tensioni:
Uo = 2,560 + 0,120 = 2,68 V
3. Un metodo che viene spesso impiegato per risolvere problemi di questo tipo è quello che sfrutta il
principio di sovrapposizione degli effetti. In questo caso viene portato alto (a URIF) un solo ingresso
alla volta mentre gli altri due sono tenuti al livello logico basso (la massa) e si calcola la
corrispondente tensione d’uscita.
a) All’ingresso impostiamo il codice 100.
Il circuito diviene quello mostrato nella figura 2. La resistenza equivalente di tutta la rete a sinistra
della sezione AA è:
2R // 2R  R// 2R R
 2R
e quindi la tensione del generatore equivalente vale:
Eeq' 
U RIF
U
 2R  RIF  2,5 V
2R  2R
2
3
Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
Fig. 2.
Poiché l’amplificatore operazionale è montato in configurazione non invertente, il suo guadagno di
tensione è pari a:
ACL  1 
RF
2
R1
La tensione d’uscita vale:
U O'  Eeq'  ACL  2,5  2  5 V
b) All’ingresso impostiamo il codice 010
Il circuito diviene quello mostrato nella figura 3a. La resistenza equivalente di tutta la rete a sinistra
della sezione BB è:
(2R // 2R) + R = 2R
ottenendo la figura 3b.
4
Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
Fig. 3a
Fig. 3ba
Applicando il teorema di Thevenin alla rete a sinistra della sezione CC, otteniamo (fig. 3c):
Req' '  R
Eeq' ' 
U RIF
 1,25 V
4
La tensione all’uscita dell’amplificatore operazionale risulta, dunque:
U O' '  Eeq' '  ACL  1,25  2  2,5 V
5
Mi preparo per la verifica
Marco Coppelli - Bruno Stortoni
c) All’ingresso impostiamo il codice 001.
Il circuito diviene quello mostrato nella figura 4. L’applicazione del teorema di Thevenin al circuito
in esame, fatta per passi successivi, porta a calcolare un generatore equivalente avente resistenza
Req' ' '  R e tensione:
Eeq' ' ' 
U RIF
 0,625 V
8
La tensione all’uscita dell’operazionale risulta, in questo caso:
U O' ' '  Eeq' ' '  ACL  0,625  2  1,25 V
Fig. 4.
La tensione totale d’uscita dal convertitore è il risultato della sovrapposizione delle tensioni relative
ai bit che sono posti ad 1.
6