ESAME di STATO 2002
Disegni a cura del prof. Cristiano DOMENICHELLI
Testi della prof.ssa Tiziana LA TORELLA
LICEO SCIENTIFICO “GALILEO FERRARIS”
1
ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Sessione 2002
Indirizzo: SCIENTIFICO
Tema di : MATEMATICA
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.
PROBLEMA 2
Si considerino le lunghezze seguenti:
dove
è una lunghezza nota non nulla ed
a) Determinare per quali valori di
triangolo non degenere.
è una lunghezza incognita.
le lunghezze [1] si possono considerare quelle dei lati di un
b) Stabilire se, fra i triangoli non degeneri i cui lati hanno le lunghezze [1], ne esiste uno di area
massima o minima.
c) Verificato che per
le [1] rappresentano le lunghezze dei lati di un triangolo,
descriverne la costruzione geometrica con riga e compasso e stabilire se si tratta di un triangolo
rettangolo, acutangolo o ottusangolo.
d) Indicato con ABC il triangolo di cui al precedente punto c), in modo che BC sia il lato
maggiore, si conduca per A la retta perpendicolare al piano del triangolo e si prenda su di essa
un punto D tale che AD sia lungo
: calcolare un valore approssimato a meno di un grado
(sessagesimale) dell’ampiezza dell’angolo formato dai due piani DBC e ABC.
Breve spiegazione :
Il problema presenta alcuni quesiti di geometria piana, in particolare:
a) chiede le condizioni per l’esistenza di un triangolo non degenere
( la lunghezza di ciascun lato positiva e il verificarsi delle disuguaglianze triangolari);
b) si deve determinare l’area di un triangolo, noti solo i lati ( formula di Erone)
e la derivata per calcolare l’area massima;
c) è richiesta la costruzione con riga e compasso di triangoli (rettangolo, acutangolo e
ottusangolo) , considerando le relazioni tra triangoli e angoli alla circonferenza
e al centro in una semicirconferenza.
d) per calcolare l’ angolo tra due piani si determina l’angolo tra le due altezze dei triangoli
appartenenti ai due piani.
2
a) Determinare per quali valori di
le lunghezze [1]
si possono considerare quelle dei lati di un triangolo non degenere.
Le lunghezze ,
del triangolo non
degenere ABC devono essere
e ogni lunghezza
deve verificare
il teorema sulle disuguaglianze
triangolari
S1 =
Esistenza dei lati
#a + 2 x < ( a $ x ) + ( 2 a $ x )
S2 = "
!a + 2 x > ( 2 a $ x ) $ ( a $ x )
S = S1 ! S 2
Esistenza del triangolo non degenere
&
S = %(x ' R / 0 < x <
$
3
a#
"
2!
punto a)
b) Stabilire se, fra i triangoli non degeneri i cui lati hanno le lunghezze [1],
ne esiste uno di area massima o minima.
Per determinare l’area di un triangolo ABC,
noti solo i lati,
è preferibile utilizzare
la FORMULA DI ERONE
A=2
P&P
#& P
#& P
#
$ ' a !$ ' b !$ ' c !
2%2
"% 2
"% 2
"
A = 2 2a(2a ! a ! 2 x )(2a ! a + x )(2a ! 2a + x )
y = 2 2a 3 x ! 2a 2 x 2 ! 4ax 3
VALORE MASSIMO
per
x=
2
7 !1
a
6
punto b)
La formula classica dell’area
e la formula trigonometrica
non possono essere applicate in modo immediato.
4
c) Verificato che per
le [1] rappresentano le lunghezze dei lati di un triangolo,
descriverne la costruzione geometrica con riga e compasso
e stabilire se si tratta di un triangolo rettangolo, acutangolo o ottusangolo.
Un triangolo acutangolo non
puo’ essere inscritto in una
semicirconferenza
avente il lato maggiore BC
come diametro
perché il vertice A risulta esterno.
Ogni triangolo rettangolo
è inscritto in una semicirconferenza
avente il lato maggiore BC
come diametro
e il vertice A
appartenente alla circonferenza
Un triangolo ottusangolo non
puo’ essere inscritto in una
semicirconferenza
avente il lato maggiore BC
come diametro
perché il vertice A risulta interno.
Per
la costruzione con riga e compasso
determina un triangolo ABC ottusangolo
punto c)
5
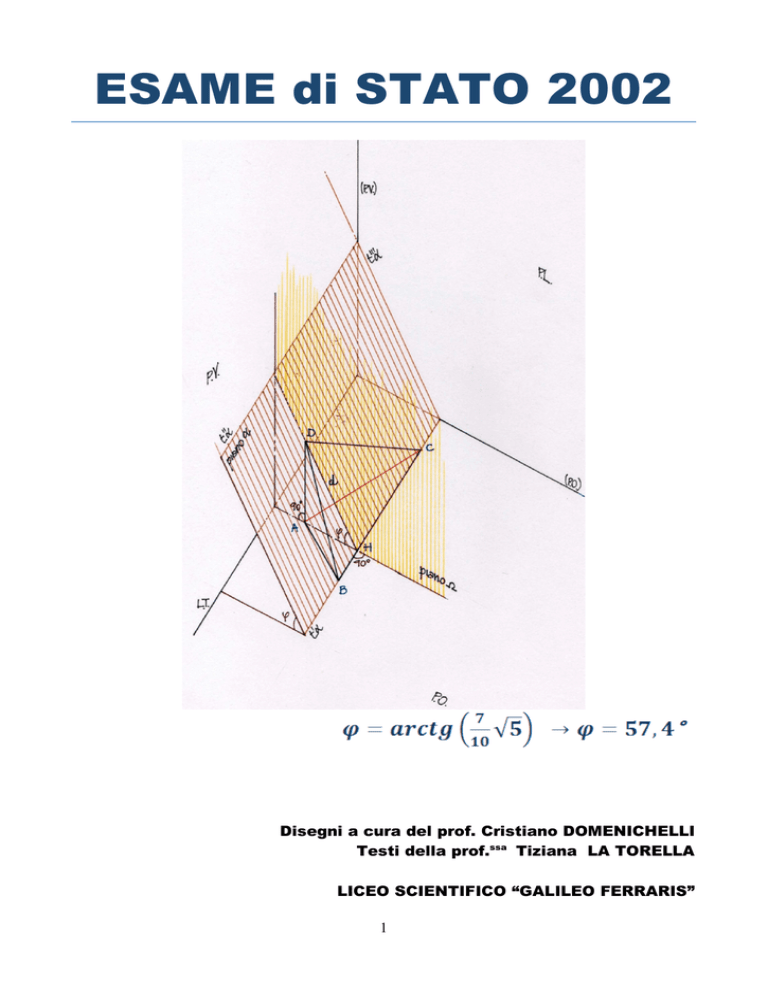
c) Indicato con ABC il triangolo di cui al precedente punto c),
in modo che BC sia il lato maggiore, si conduca per A la retta perpendicolare al piano
del triangolo e si prenda su di essa un punto D tale che AD sia lungo
:
calcolare un valore approssimato a meno di un grado (sessagesimale) dell’ampiezza
dell’angolo formato dai due piani DBC e ABC.
Tracciate le altezze dei triangoli ABC e BCD si calcola l’angolo AHD ,
considerando i teoremi sui triangoli rettangoli applicati al triangolo AHD.
punto d)
6











