Cinematica del Punto

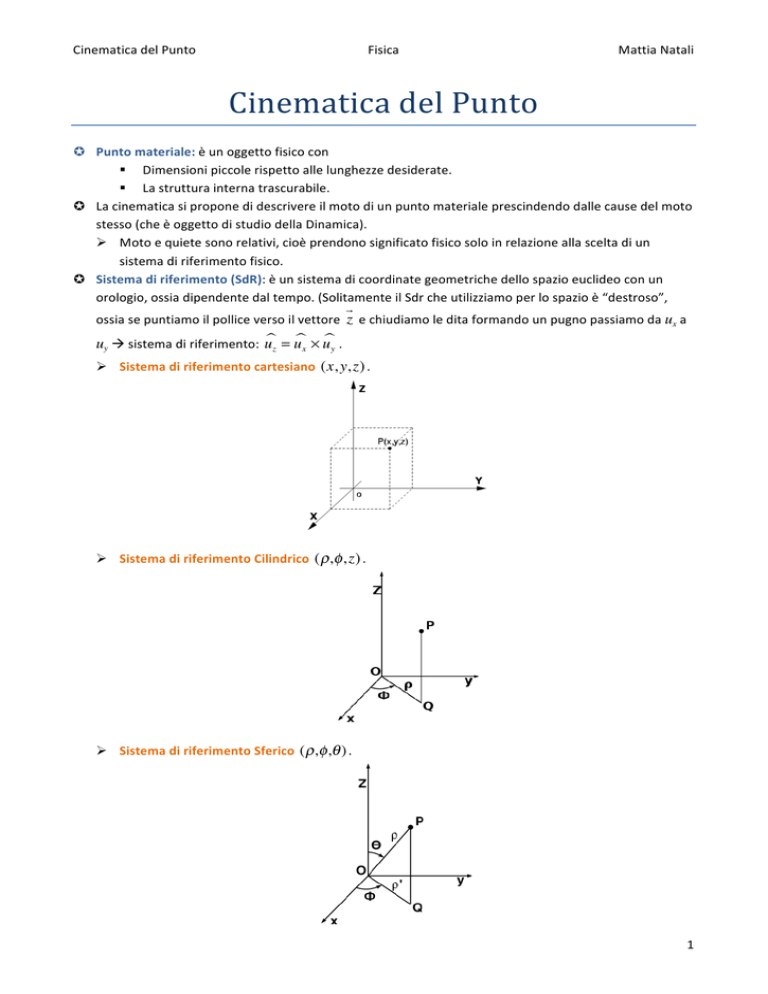
Cinematica del Punto Fisica Mattia Natali Cinematica del Punto  Punto materiale: è un oggetto fisico con  Dimensioni piccole rispetto alle lunghezze desiderate.  La struttura interna trascurabile.  La cinematica si propone di descrivere il moto di un punto materiale prescindendo dalle cause del moto stesso (che è oggetto di studio della Dinamica).  Moto e quiete sono relativi, cioè prendono significato fisico solo in relazione alla scelta di un sistema di riferimento fisico.  Sistema di riferimento (SdR): è un sistema di coordinate geometriche dello spazio euclideo con un orologio, ossia dipendente dal tempo. (Solitamente il Sdr che utilizziamo per lo spazio è “destroso”, 
ossia se puntiamo il pollice verso il vettore z e chiudiamo le dita formando un pugno passiamo da ux a uy  sistema di riferimento: uz = ux × uy .  Sistema di riferimento cartesiano (x, y, z) .  Sistema di riferimento Cilindrico ( ρ, φ , z) .  Sistema di riferimento Sferico ( ρ, φ ,θ ) . 1 Cinematica del Punto Fisica Mattia Natali  Legge oraria del moto di un punto materiale: è l’insieme delle relazioni che assegnano in funzione del tempo le coordinate della posizione occupata dal punto in movimento. Alcuni esempi di sistemi che rispettano la legge oraria: ⎧ x = x(t)
⎪
 ⎨ y = y(t) ⎪ z = z(t)
⎩
t ∈[t1 ,t 2 ] . Sistema di riferimento cartesiano. ⎧r = r(t)
⎪
 ⎨ϕ = ϕ (t) ⎪ z = z(t)
⎩
t ∈[t1 ,t 2 ] . Sistema di riferimento cilindrico.  Se combino x(t), y(t) e z(t) tra loro esplicitando t da una equazione e sostituendolo nelle altre trovo una relazione matematica tra x, y, z del tipo F(x, y, z) = 0 detta equazione della traiettoria del punto materiale.  Traiettoria del moto: insieme di tutti i punti (x, y, z) dello spazio occupati dal punto materiale durante il moto. I principali tipi di moti sono:  Moto rettilineo: quando la traiettoria giace su una retta.  Moto circolare: quando la traiettoria giace su una circonferenza.  Moto curvilineo: quando la traiettoria giace su una generica curva.  Ascissa curvilinea: è la distanza curvilinea del punto materiale rispetto all’origine dell’ascissa curvilinea presa con segno positivo se questa distanza è nella direzione del verso, negativa il contrario.  L’origine dell’ascissa curvilinea NON deve essere per forza il luogo in cui vi è il punto materiale all’istante t = 0; sono due cose completamente distinte.  Velocità:  Velocità media: 
Definizione: La velocità scalare media in un certo intervallo di tempo è data dal rapporto tra la lunghezza del tratto di traiettoria percorso in tale intervallo di tempo e l’intervallo di tempo stesso. 
Equazione: vm (t1 ,t 2 ) =

Dimensioni: [Vm ] = [L][T ]−1 . 
Se vm (t1 ,t 2 ) = vm costante ∀t1 ,t 2  moto uniforme. Nella rappresentazione del diagramma s(t 2 ) − s(t1 ) ∆ s(t1 ,t 2 )
. =
t 2 − t1
∆t
orario il moto uniforme è rappresentato da una retta di coefficiente angolare v (costante).  Velocità istantanea: 
s(t + ∆ t) − s(t) ds(t) s(t + ∆ t) − s(t) s(t 2 ) − s(t1 )
=
, . =
∆ t →0
∆t
dt
∆t
t 2 − t1
Equazione: v(t) = lim
Ossia v(t1 ) = lim vm (t1 ,t 2 ) è la velocità media in un intervallo di tempo che tende a 0. t 2 →t1

La velocità istantanea all’istante t coincide con la retta tangente alla curva s(t) all’istante t

considerato. Calcolo della legge oraria a partire dalla conoscenza della velocità istantanea. • Sia noto v(t)∀t ∈[t1 ,t 2 ] e sia noto s(t = t 0 ) con t 0 ∈[t1 ,t 2 ] . 2 Cinematica del Punto Fisica Mattia Natali t
t
ds(t)
ds(t ')
dt ' 
♦ v(t) =
 integro entrambi i membri ∫ v(t ')dt ' = ∫
dt
dt '
t0
t0
t
t
t
t
∫ v(t ')dt ' = ∫ ds(t ')  ∫ v(t ')dt ' =s(t) − s(t0 )  s(t) = s(t0 ) + ∫ v(t ')dt ' con
t0
t ∈[t1 ,t 2 ] . Lo spazio percorso è misurato dall’area della superficie racchiusa dal grafico t0
t0
t0
velocità scalare-­‐tempo, dall’asse dei tempi e dalle rette perpendicolari all’asse dei tempo nei punti di ascissa t0 e t1 più la quantità scalare s0.  Accelerazione:  Accelerazione media: v(t 2 ) − v(t1 ) ∆ v(t1 ,t 2 )
. =
t 2 − t1
∆t

Equazione: am (t1 ,t 2 ) =

Dimensioni: [am ] = [V ][T ]−1 = [L][T ]−2 . 
Se am (t1 ,t 2 ) = a costante ∀t1 ,t 2  moto uniformemente accelerato. 
Legge oraria del moto uniformemente accelerato: t
t
1
s(t) = s(0) + ∫ v(t ')dt ' = s(0) + ∫ ( v(0) + at ') dt ' = s(0) +v(0)t + at 2 ricorda che 2
0
0
v(t ') = v(0) + at ' .  Accelerazione istantanea: v(t + ∆ t) − v(t) dv(t)
v(t ) − v(t1 )
 Equazione: a(t) = lim
=
= lim 2
= lim am (t1 ,t 2 ) . ∆ t →0
t 2 →t1
t 2 →t1
∆t
dt
t 2 − t1
 Rappresenta la retta tangente alla curva v(t) all’istante t. 

d 2 s(t)
dv(t) d ⎛ ds(t) ⎞
⎛ ds(t) ⎞
= ⎜
Osservazione: a(t) =
. ⎟ siccome v(t) = ⎜⎝
⎟  a(t) =
dt
dt ⎝ dt ⎠
dt ⎠
dt 2
Calcolo della legge della velocità a partire dalla accelerazione: • Sia noto a(t)∀t ∈[t1 ,t 2 ] e sia noto v(t 0 )∀t 0 ∈[t1 ,t 2 ] . t
t
t
t
dv(t)
dv(t ')
dt '  ∫ a(t ')dt ' = ∫ dv(t ') 
♦ a(t) =
 ∫ a(t ')dt ' = ∫
dt
dt '
t0
t0
t0
t0
t
∫ a(t ')dt ' =v(t) − v(t
0
)  t0
t
♦
v(t) = v(t 0 ) + ∫ a(t ')dt ' ∀t ∈[t1 ,t 2 ] t0

Calcolo della legge oraria a partire dalla accelerazione: • Sia noto a(t)∀t ∈[t1 ,t 2 ] , v(t 0 ) con t 0 ∈[t1 ,t 2 ] e inoltre sia noto s(t 0 ) con t 0 ∈[t1 ,t 2 ] 3 Cinematica del Punto Fisica t
•
∫
Mattia Natali t
∫
Sostituisco v(t) = v(t 0 ) + a(t ')dt ' in s(t) = s(t 0 ) + v(t ')dt '  t0
t0
⎛t
⎞
s(t) = s(t 0 ) + ∫ v(t 0 )dt '+ ∫ ⎜ ∫ a(t '')dt ''⎟ dt ' 
⎠
t0
to ⎝ t0
t
t
t ⎛ t
⎞
s(t) = s(t 0 ) + v(t 0 )(t − t 0 ) + ∫ ⎜ ∫ a(t '')dt ''⎟ dt ' . ⎠
to ⎝ t0
 Moto uniformemente accelerato: s(t) = s(t 0 ) + v(t 0 )(t − t 0 ) +
1
a(t − t 0 )2 . 2
 La dinamica si occupa di determinare a(t) in [t1 ,t 2 ] .  Moto del punto materiale in tre dimensioni:  Raggio vettore di un punto materiale in un dato sistema di riferimento: è il vettore dello spazio euclideo che ha per componenti le coordinate cartesiane del punto geometrico occupato in un dato istante dal punto materiale. 


Il modulo di r è r = r =

Il raggio vettore può essere definito: •
•
x 2 + y 2 + z 2 . 
r = xux + yuy + zuz . 
r definito con α , β , γ  cos 2 α + cos 2 β + cos 2 γ = 1 . 
♦ cos α = coseno direttore di r rispetto a x . 
♦ cos β = coseno direttore di r rispetto a y . 
♦ cos γ = coseno direttore di r rispetto a z . ♦
x = r cos α , y = r cos β , z = r cos γ .  Velocità vettoriale:  Velocità vettoriale media: 




r (t 2 ) − r (t1 ) ∆ r (t1 ,t 2 )
=
 Equazione: vm (t1 ,t 2 ) =
. t 2 − t1
∆t
 Velocità vettoriale istantanea: 



r (t + ∆ t) − r (t) dr (t)
=
 Equazione: v(t) = lim
. ∆ t →0
∆t
dt



• Osservazione: v(t) = lim vm (t1 ,t 2 ) . t 2 →t1
4 Cinematica del Punto 

Mattia Natali (
)
d
vx (t)ux + vy (t)uy + vz (t)uz =
x(t)ux + y(t)uy + z(t)uz  dt
d
d
d
x(t)ux +
y(t)uy +
z(t)uz i versori sono costanti, quindi la loro derivata è 0  dt
dt
dt
dx(t)
⎧
⎪vx (t) = dt
⎪
dx(t)  dy(t)  dz(t) 
dy(t)
⎪
ux +
uy +
uz  ⎨vy (t) =
. dt
dt
dt
dt
⎪
dz(t)
⎪
⎪⎩vz (t) = dt



dr (t)
dr (t) è tangente alla traiettoria in P(t)  v(t) =
. dt

⎛ ds(t) ⎞
Legame esistente tra v(t) e v(t) ⎜ =
⎟ : ⎝
dt ⎠

dr (t) = ds perché se ∆ t → 0 = dt la traiettoria “si confonde” con il vettore  •

dr (t) = ds(t)uT (t)  se dividiamo entrambi i membri per dt abbiamo 



dr (t) ds(t) 
dr (t)
=
uT (t) , siccome v(t) =
 v(t) = v(t)uT (t)  il legame tra velocità dt
dt
dt

vettoriale e velocità scalare è quindi v(t) = v(t)u (t) . u (t) è il versore tangente alla (

Fisica )
(
)
(
)
T


T
traiettoria in t. ♦ Nella velocità media NON vale tale proprietà, in questo caso infatti ∆t non tende a 0. Il modulo della velocità vettoriale istantanea NON è sempre uguale alla velocità scalare istantanea perché la velocità scalare può essere negativa, mentre il modulo è sempre positivo. 

Sia nota v(t)∀t ∈[t1 ,t 2 ] e sia noto r (t = t 0 ) con t 0 ∈[t1 ,t 2 ] posso determinare la legge oraria 
r (t)∀t ∈[t1 ,t 2 ] . 

t
t


dr (t)
dr (t ')
dt ' 
• v(t) =
 integro entrambi i membri ∫ v(t ')dt ' = ∫
dt
dt '
t0
t0
t
t
t







v
(t
')dt
'
=
dr
(t
')
v(t
')dt
'
=
r
(t)
−
r
(t
)
r
(t)
=
r
(t
)
+
v


0
0
∫
∫
∫
∫ (t ')dt ' . t



r (t) = r (t 0 ) + v(t − t 0 ) legge oraria di un moto rettilineo uniforme. t0

t0
t0
t0
 Accelerazione vettoriale:  Accelerazione vettoriale media: 



v(t 2 ) − v(t1 ) ∆ v(t1 ,t 2 )
=
 Equazione: am (t1 ,t 2 ) =
. t 2 − t1
∆t


 Se am (t1 ,t 2 ) = a costante ∀t1 ,t 2  moto uniformemente accelerato.  Accelerazione istantanea: 5 Cinematica del Punto 



Fisica Mattia Natali 






v(t + ∆ t) − v(t) dv(t)
v(t 2 ) − v(t1 )
=
= lim
= lim am (t1 ,t 2 ) . Equazione: a(t) = lim
∆ t →0
t 2 →t1
t 2 →t1
∆t
dt
t 2 − t1





⎛ dr (t) ⎞ 
d 2 r (t)
dv(t) d ⎛ dr (t) ⎞
= ⎜
Osservazione: a(t) =
siccome v(t) = ⎜
 a(t) =
. dt 2
dt
dt ⎝ dt ⎟⎠
⎝ dt ⎟⎠
⎧
dvx (t) d ⎛ dx(t) ⎞ d 2 x(t)
a
(t)
=
= ⎜
=
⎪ x
⎝ dt ⎟⎠
dt
dt
dt 2
⎪

dvy (t) d ⎛ dy(t) ⎞ d 2 y(t)
⎪
d 2 x(t)  d 2 y(t) 
d 2 z(t) 
a
(t)
=
u
+
u
+
u z = ⎜
=

y
⎨ay (t) =
⎟
x
dt
dt ⎝ dt ⎠
dt 2
dt 2
dt 2
dt 2
⎪
⎪
dvz (t) d ⎛ dz(t) ⎞ d 2 z(t)
= ⎜
⎪az (t) =
⎟=
dt
dt ⎝ dt ⎠
dt 2
⎩

Decomposizione in componenti N e T (Normale e Tangenziale): v(t) = v(t)uT (t) . Se faccio la derivata trovo l’accelerazione  (
)



⎛ duT (t) ⎞
dv(t) d v(t)uT (t) ⎛ dv(t) ⎞ 
a(t) =
=
=⎜
u
(t)
+
v(t)
⎜ dt ⎟ 
⎝ dt ⎟⎠ T
dt
dt
⎝
⎠

du (t)
a(t) = a(t)uT (t) + v(t) T . Ora che abbiamo trovato la componente tangenziale dt
a(t)uT (t) dobbiamo trovare la componente normale scrivendo in modo diverso il secondo 

addendo. Per definizione di differenziale duT (t) = uT (t + dt) − u
T (t) e questa differenza quando ∆ t → 0 = dt è perpendicolare al versore uT (t) ed è quello che stavamo cercando. ds
ds 
ds 
u N (t)  duT (t) = dϑ , dϑ =
 duT (t) =
. duT (t) =
ρ
ρ
ρ

duT (t)
ds 
ds(t) 1 
v 2 (t) 
=
u N (t) =
u N (t)  a(t) = a(t)uT (t) +
u N (t) . dt
ρ(t)dt
dt ρ(t)
ρ(t)


• Accelerazione tangenziale: a(t)u (t) = a  riguarda la velocità scalare, il modulo del T
T
vettore velocità con segno positivo se è concorde con l’ascissa curvilinea, negativo viceversa. •
•

v 2 (t) 
u N (t) = aN  riguarda la direzione del vettore velocità. ρ(t)
ρ(t) è il raggio della circonferenza che meglio approssima la traiettoria nel punto P(t) . E Accelerazione normale: questa circonferenza si chiama cerchio osculatore della traiettoria ed è sempre dalla parte concava. 

⎧⎪aT = 0
♦ Se ⎨   ∀t  moto con velocità scalare costante (lungo tutta la traiettoria).  ⎩⎪a = aN (t)




v(t1 ) = v(t 2 )  v(t1 ) = v(t 2 ) . 
⎧⎪aN = 0
♦ Se ⎨  
 ∀t  moto rettilineo. ⎩⎪a = aT (t)
6 Cinematica del Punto 
Fisica Mattia Natali Calcolo della legge oraria a partire dalla accelerazione: 


•
Sia noto a(t)∀t ∈[t1 ,t 2 ] , v(t 0 ) con t 0 ∈[t1 ,t 2 ] e inoltre sia noto r (t 0 ) con t 0 ∈[t1 ,t 2 ] •
t
t






Sostituisco v(t) = v(t 0 ) + ∫ a(t ')dt ' in r (t) = r (t 0 ) + ∫ v(t ')dt '  t0
t0
t
t ⎛ t
⎞




r (t) = r (t 0 ) + ∫ v(t 0 )dt '+ ∫ ⎜ ∫ a(t '')dt ''⎟ dt ' 
⎠
t0
to ⎝ t0
t ⎛ t
⎞




r (t) = r (t 0 ) + v(t 0 )(t − t 0 ) + ∫ ⎜ ∫ a(t '')dt ''⎟ dt ' . ⎠
to ⎝ t0
 Vari tipi di moti:  Moto rettilineo: 




dr
(t)
dx(t)
dv
(t) d 2 x(t) 
=
ux  a(t) =
=
u x .  Sapendo che r (t) = x(t)ux e v(t) =
dt
dt
dt
dt 2


 Moto rettilineo uniforme: significa che v(t) = v costante  x(t) = x0 + v(t) , in forma 
vettoriale r (t) = (x0 + vt)ux .  Moto Circolare: 
Velocità angolare scalare: misura la velocità con cui varia l’angolo θ formato dal vettore di 
1 ∆ s ∆θ v
=
= . R ∆t ∆t R
dθ
La velocità angolare ω è un vettore avente come modulo , direzione perpendicolare al dt
piano contenente la traiettoria e verso tale che, rispetto ad un osservatore disposto come ω , il posizione OP con l’asse di riferimento  ω =

punto ruota in senso antiorario.  r = ρ (t) costante (raggio della traiettoria). 


r (t) = RuR con uR versore radiale. 


v(t) = v(t)uT (t) = ω (t) × R(t) con la regola della mano destra possiamo verificare che effettivamente il prodotto vettoriale ha 
lo stesso verso e direzione di v(t) . ds(t)
dϑ (t)
dϑ (t)
=R
= ω (t)R (NB: ω (t) =
) dt
dt
dt

 ω (t) = ω (t)uz velocità angolare vettoriale. [ω ] = [rad/s] . In 
questa immagine ω parte da A e punta “verso di noi”. 


Se aT = 0  v(t) = costante  w(t) = costante. 



v 2 (t)  v 2 (t) 
uN =
u N = ω 2 RuN . (NB: a non è costante, è costante Se a(t) = aN (t)  aN (t) =
ρ(t)
R



v(t) =
solamente il suo modulo!). 7 Cinematica del Punto 
Fisica Mattia Natali Moto periodico: un moto si definisce tale di periodo T quando esiste un 

2π
T ∈ + : r (t + T ) = r (t) . Il moto circolare uniforme è periodico di periodo T =
. Infatti ω
2π
2π
ϑ (t) = ϑ 0 + ω t mentre ϑ (t +
) = ϑ0 + ωt + ω
= ϑ 0 + ω t + 2π . Gli angoli discostano ω
ω
di un angolo giro, ossia il punto torna sempre al punto di partenza periodicamente. 

La frequenza di un moto periodico di periodo T è ν =
1
−1
[ν ] = [s ] = [Hz] . T


dω (t)
Accelerazione angolare vettoriale: α (t) =
. Per il moto circolare sappiamo che dt


dϑ (t) 
d ⎛ dϑ (t) ⎞  d 2ϑ (t) 
uz . Perciò l’accelerazione ω (t) = ω (t)uz =
uz quindi a(t) = ⎜
⎟ uz =
dt ⎝ dt ⎠
dt 2
dt
angolare vettoriale è parallela alla velocità angolare vettoriale (infatti hanno lo stesso versore). 





dv(t) d  
dω   d R
dω 
a(t) =
=
ω×R =
× R+ω ×
= α (t)  , ricordando che dt
dt
dt
dt
dt










a(t) = α (t) × R(t) + ω (t) × v(t) = α (t) × R(t) + ω (t) × ω (t) × R(t) . 







ω (t) × ω (t) × R(t) = aN . • α (t) × R(t) = aT (
)
(
(
)
)
 Moto armonico semplice: 
È un moto unidimensionale con legge oraria sinusoidale x(t) = Asin(ω t + ϕ ) . •
•
•



2π
dove T è il periodo del moto. T
ω t + ϕ : fase. ϕ : costante di fase. ω : pulsazione. ω=
dx(t)
π
π⎞
⎛
= Aω cos(ω t + ϕ ) è sfasata di rispetto alla x(t)  Aω sen ⎜ ω t + ϕ + ⎟ . ⎝
2⎠
dt
2
dv(t)
a(t) =
= −Aω 2 sin(ω t + ϕ ) è sfasata di π dispetto alla x(t)  Aω 2 sin (ω t + ϕ + π ) . dt
d 2 x(t)
d 2 x(t)
2
= −ω x(t)  + ω 2 x(t) = 0 equazione del moto armonico Osservazione: 2
2
dt
dt
semplice di pulsazione ω . v(t) =
8