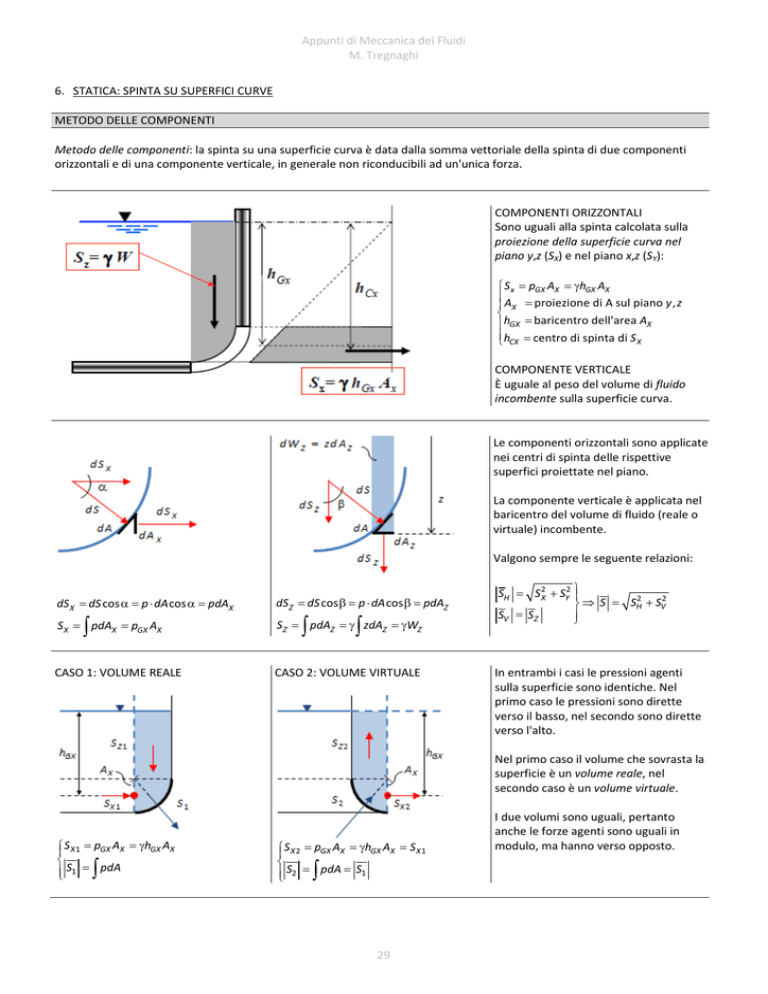
Appunti di Meccanica dei Fluidi M. Tregnaghi 6. STATICA: SPINTA SU SUPERFICI CURVE METODO DELLE COMPONENTI Metodo delle componenti: la spinta su una superficie curva è data dalla somma vettoriale della spinta di due componenti orizzontali e di una componente verticale, in generale non riconducibili ad un'unica forza. COMPONENTI ORIZZONTALI
Sono uguali alla spinta calcolata sulla proiezione della superficie curva nel piano y,z (SX) e nel piano x,z (SY): S x pGX AX hGX AX
A proiezione di A sul piano y , z
X
hGX baricentro dell'area AX
hCX centro di spinta di S X
COMPONENTE VERTICALE È uguale al peso del volume di fluido incombente sulla superficie curva. dS X dS cos p dA cos pdAX
S X pdAX pGX AX
dSZ dS cos p dA cos pdAZ
CASO 1: VOLUME REALE S X 1 pGX AX hGX AX
S1 pdA
S Z pdAZ zdAZ WZ
CASO 2: VOLUME VIRTUALE
S X 2 pGX AX hGX AX S X 1
S2 pdA S1
29 Le componenti orizzontali sono applicate nei centri di spinta delle rispettive superfici proiettate nel piano. La componente verticale è applicata nel baricentro del volume di fluido (reale o virtuale) incombente. Valgono sempre le seguente relazioni: SH S 2X SY2
2
2
S SH SV SV SZ
In entrambi i casi le pressioni agenti sulla superficie sono identiche. Nel primo caso le pressioni sono dirette verso il basso, nel secondo sono dirette verso l'alto. Nel primo caso il volume che sovrasta la superficie è un volume reale, nel secondo caso è un volume virtuale. I due volumi sono uguali, pertanto anche le forze agenti sono uguali in modulo, ma hanno verso opposto. Appunti di Meccanica dei Fluidi M. Tregnaghi METODO DELL'EQUILIBRIO GLOBALE Metodo dell'equilibrio globale: la spinta del fluido su una superficie curva (bi‐dimensionale) è uguale e contraria alla reazione che la superficie esercita su un determinato volume di controllo opportunamente scelto. Metodo dell'equilibrio globale (M.e.g.):
1) Si determina un opportuno volume di controllo, in modo da calcolare agevolmente le spinte che agiscono sul volume. 2) Per l'equilibrio alla traslazione deve risultare: i G 0 0
S
i G
S 0
Metodo delle componenti
S X pGX AX
R
H RB
2
S Z WZ ,REALE
HR 1 R2 B
4
Metodo equilibrio globale
R
1 pG1 A1 H 2 R 2B
G 1 R2 R2 2 B
2
1 X 1 cos 4 H R 2 RB
1 Z 1 sin 4 H R 2 RB
S H R RB
1X
X
2
S Z 1 Z G
1 2
HR R2 2 B R R2 2 B
4
NOTA In generale le tre componenti della spinta agente su una superficie curva non sono complanari. SV SZ vale solo se S X e SY sono complanari. In caso contrario, si pone
SH SX' SY dove SX' è uguale in Affinché il sistema sia nuovamente in equilibrio si deve aggiungere una nuova coppia di forze SZ' di momento pari a MSZ SZ' dZ MSX . In generale, SZ' non sarà complanare alla forza orizzontale. Quindi il sistema è riconducibile a: '
modulo, direzione e verso a SX , ma S S X SY
2 forze non complanari H
viene 'traslata' dal piano 1 al piano 2 '
SV SZ SZ
dove giace la componente SY . Il nuovo oppure sistema di forze genera un momento di S SH SV'
'
'
1 forza + 1 momento coppia SX pari a MSX SX d X .
'
M con M SV dV
30 Appunti di Meccanica dei Fluidi M. Tregnaghi CONFRONTO TRA I DUE METODI In molti casi i 2 metodi risultano equivalenti dal punto di vista del calcolo delle forze. Per il metodo delle componenti è necessario individuare i volumi incombenti, per il metodo dell'equilibrio globale si deve individuare il volume di controllo. CASO 1: SUPERFICIE IN PRESSIONE
Metodo delle componenti SZ WZ ,VIRTUALE
2
hD 1 D B
2 4
Metodo equilibrio globale SZ 1 G
2
h DB 1 D B
2 4
In questo caso il M.e.g. è equivalente al metodo dei fluidi incombenti (ovvero al metodo delle componenti). Il volume incombente è legato al volume di controllo secondo la seguente relazione:
WZ ,VIRTUALE W1 WCONTROLLO
2
hD B 1 D B
2 4
dove W1 1
CASO 2: SUPERFICIE IN DEPRESSIONE
Metodo delle componenti SZ WZ ,REALE
2
hD 1 D B
2 4
Metodo equilibrio globale SZ 1 G
2
h DB 1 D B
2 4
Anche in questo caso i due metodi risultano equivalenti. Il volume incombente è legato al volume di controllo secondo la seguente relazione:
WZ ,REALE W1 WCONTROLLO
2
hD B 1 D B
2 4
dove W1 1
CASO 3: PARZIALMENTE IN PRESSIONE
Metodo delle componenti SZ WZ ,VIRTUALE WZ ,REALE
2 WZ 1 WZ 2
Metodo equilibrio globale SZ 1 G
2
h DB 1 D B
2 4
Nota: Nei tre casi esaminati il volume di controllo scelto è sempre lo stesso. 31 In questo caso è conveniente usare il M.e.g., in quanto il calcolo dei diversi volumi risulterebbe laborioso. Non appare immediatamente evidente la relazione tra volume incombente e volume di controllo, come illustrato graficamente. Appunti di Meccanica dei Fluidi M. Tregnaghi 7. STATICA: GALLEGGIAMENTO E STABILITÀ SPINTA DI GALLEGGIAMENTO Un corpo immerso in un fluido subisce una spinta verso l'alto (spinta di galleggiamento) pari al peso del volume di fluido spostato dal corpo. FORZE ORIZZONTALI Le spinte elementari dFX giacenti su un piano orizzontale alla quota z si bilanciano in quanto: 1) p1 z p2 z uguale pressione 2) dAX 1 dAX 2 dAX uguale area Da cui risulta: dFX 1 dFX 2 dFX 0 FORZE VERTICALI METODO DEI FLUIDI INCOMBENTI
Le spinte elementari dFZ giacenti su un
F
p z dA fluido incombente 1
V1
piano verticale non si bilanciano in
S sup
quanto:
FV 2
p z dA fluido incombente 2
S
inf
1) p z2 p z1 pressione diversa 2) dAZ 1 dAZ 2 dAZ area uguale FB FV 2 FV 1 W2 W1
Da cui risulta: FB WS
dFZ 1 dFZ 2 dFZ hdAZ METODO DI INTEGRAZIONE
FB p z dA
S
p z dA p z dA
S2
S1
p z
2
p z1 dA
Sz
z
2
z1 dA hdA
Sz
Sz
FB WS
AFFONDAMENTO E EMERSIONE
In base alla differenza di densità tra fluido e corpo si possono avere le seguenti situazioni: S FB GS affondamento
S FB GS emersione
F G equilibrio
S
B
S
CORPO PARZIALMENTE IMMERSO
Se la densità del corpo è inferiore a quella del fluido, il corpo risulta immerso parzialmente. La forza di galleggiamento eguaglia il peso del corpo e il volume di carena (volume immerso) risulta: FB WC
S
FB G S WC WS
GS SWS
FB = spinta di galleggiamento (buoyancy) Nel secondo caso, il corpo emergerà fino WC = volume di carena (vol. immerso) La spinta di galleggiamento è applicata a raggiungere una condizione di C = baricentro del volume di carena nel centro di carena (= baricentro di WC).
equilibrio statico. 32 Appunti di Meccanica dei Fluidi M. Tregnaghi STABILITÀ AL GALLEGGIAMENTO
Un corpo immerso può trovarsi in condizioni di equilibrio stabile, indifferente, oppure instabile. Un corpo galleggiante può trovarsi in condizioni di equilibrio stabile oppure instabile. CORPO IMMERSO (a) zG zC equilibrio stabile
(b) zG zC equilibrio indifferente (c) zG zC equilibrio instabile
Nel caso (a) ad una qualsiasi rotazione del corpo corrisponde l'instaurarsi si un momento stabilizzante. Nel caso (b) ad una qualsiasi rotazione del corpo corrisponde l'instaurarsi si un momento instabilizzante. CORPO GALLEGGIANTE M = metacentro, intersezione tra la retta di azione di FB e l'asse di galleggiamento
GC = asse di galleggiamento GM = altezza metacentrica In seguito ad una rotazione del corpo, il centro di carena si sposta perché cambia la forma del volume immerso. (b) zG zM equilibrio stabile
(c) zG zM equilibrio instabile
ALTEZZA METACENTRICA Area sommersa
prima della rotazione: (uguaglianza dei momenti statici) A1 A2 Asub ,1 xAsub ,2
xdA xdA xdA
dopo la rotazione: Asub ,1
A3
A1
A
A
A
1 3 sub ,2
0 x x dx x x dx
A3
A1
Sup. di galleggiamento
2
x dx
x 2 Ldx
AGALL = sezione del L
A1 A 3
A1 A 3
corpo intersecata dalla
2
superficie libera del x dA IR
L
L
fluido AGALL
I
I
x
Momento d'inerzia CM
R R
Asub ,2 L WC
IR = momento d'inerzia di AGALL IR
GM CM CG GM
CG
WC
33
Appunti di Meccanica dei Fluidi M. Tregnaghi 8. MOTO RIGIDO DEI FLUIDI DISTRIBUZIONE DELLA PRESSIONE
Il moto rigido dei fluidi corrisponde al moto di un fluido contenuto in un recipiente che si muove con moto accelerato. La
distribuzione delle pressioni dipende, oltre che dal campo gravitazionale, anche dal campo inerziale associato al moto. Moto rettilineo accelerato Moto circolare uniforme IPOTESI
1) Il fluido si muove in maniera solidale con il suo recipiente. 2) Non vi sono scorrimenti relativi tra le particelle di fluido. 3) Non si generano sforzi tangenziali all'interno del fluido. v x 0
0 (1) Traslazione
v y 0
vy
v
0 (2) Rotazione x
y
x
Teorema della quantità di moto:
Fm
Fs ma
d
r
r a a0
dt
moto
moto
moto
rettilineo
circolare
circolare
accelerato
uniforme
accelerato
p h a
p g a
h g
In generale non vale la legge idrostatica.
CASO 1: MOTO VERITICALE
L'unica componente dell'accelerazione è la componente verticale: a az k da cui: p x ax 0
p y ay 0
p z g az
34 Distribuzione della pressione:
p
g az z
Discesa: az 0 "fluido più leggero"
Salita: az 0 "fluido più pesante"
In particolare: az g p patm "caduta libera" Per az g il fluido si stacca dal fondo. Appunti di Meccanica dei Fluidi M. Tregnaghi CASI APPLICATIVI Le superficie isobare possono essere individuate (1) determinando il vettore gradiente di pressione in base all'equazione
vettoriale del moto rigido, oppure (2) ponendo uguale a zero l'incremento differenziale di pressione dp. p
p
2
a2x g az s
CASO 2: MOTO RETTILINEO ACCELERATO
Si assumono diverse da zero 2 componenti dell'accelerazione: a a x i az k da cui: p x ax
p y ay 0
p z g az
Distribuzione della pressione:
Lungo una superficie isobara: p
p
0 dp dx dz
x
z
ax dx g az dz
a
a
dz
x arctan x dx
g az
g az
Tutte le superfici con inclinazione θ sono superfici isobare. CASO 3: PIANO INCLINATO
L'accelerazione lungo il piano inclinato ha modulo g∙sinα e componenti: a g sin cos j g sin2 k da cui:
p x ax 0
p y ay g sin cos
2
p z g az g 1 sin
CASO 4: CENTRIFUGA
L'unica componente dell'accelerazione è la componente centripeta: a r 2 ri da cui (in coordinate cilindriche): p r ar 2 r
1
r p a 0
p z g az g
35 Distribuzione della pressione:
Lungo una superficie isobara: p
p
0 dp dy dz
y
z
g sin cos dy cos2 dz
dz
sin cos
dz
tan 2
dy
dy
cos
Tutte le superfici con inclinazione α sono superfici isobare. Distribuzione della pressione:
Lungo una superficie isobara: p
p
0 dp dr dz
r
z
2 rdr gdz
2 r 2
dz 2 r
z r
cos t dr
g
2g
Le superfici isobare sono dei paraboloidi di rotazione.












