5. Dinamica relativistica
Fino ad ora abbiamo solamente fornito una descrizione del moto, cioè uno studio
di cinematica nell’ambito della teoria relatività ristretta. È ora necessario intraprendere un tipo di lavoro diverso e riscrivere le leggi fondamentali della dinamica. What
Abbiamo bisogno di definizioni relativistiche per le grandezze della dinamica classica?
Le leggi di Newton come F ma , non possono essere valide se non troviamo una
nuova definizione per le grandezze fisiche coinvolte. Infatti, nella trasformazione relativistica delle velocità u (u ' v )/(1 u v /c 2 ) figura una complicata dipendenza
dalla velocità relativa v , mentre nelle trasformazioni di Galileo abbiamo una semplice addizione: u u ' v .
Questo significa che, mentre in fisica classica
l’accelerazione mantiene lo stesso valore quando passiamo da un riferimento a un
altro (in moto rettilineo uniforme rispetto al primo), in fisica relativistica
l’accelerazione avrà una complessa dipendenza dalla velocità relativa v . Ma la forza
ha una sua definizione operativa indipendente (per mezzo di un dinamometro).
Non c’è motivo per cui - allo scopo di mantenere invariata la forma della seconda
legge di Newton, - una scala di forze stabilita in un sistema di riferimento, se usata in
un riferimento differente produca valori che cambiano seguendo le stesse regole
dell’accelerazione. Pertanto la seconda legge della dinamica dovrà essere riformulata
nell’ambito della teoria della relatività. I fisici esprimono questo fatto dicendo che
l’accelerazione classica non è invariante per le trasformazioni di Lorentz.
Perché è preferibile esprimere la dinamica in termini di leggi di conservazione?
Una legge di conservazione esprime sempre un contenuto più fondamentale perché
richiede la definizione di una sola grandezza fisica. Per questo motivo nel nostro
studio della dinamica relativistica non partiremo dalla riformulazione delle leggi di
Newton, ma ci concentreremo sul principio di conservazione della quantità di moto. In
accordo con il principio di relatività di Einstein, assumeremo che il principio di conservazione della quantità di moto non è un caso fortuito che si manifesta solo nel sistema di osservazione del pianeta Terra, bensì una proprietà generale che vale in
qualsiasi riferimento. Come già sappiamo dalla relatività Galileiana, energia e quantità di moto dipendono dal sistema di riferimento. Ci si convince di questo considerando che un passeggero con in mano una palla, seduto in uno scompartimento di
un treno, non attribuisce all’oggetto né quantità di moto né energia cinetica, a differenza di un altro osservatore che vede la stessa palla dalla stazione ferroviaria. Poiché il tempo e la velocità dipendono anch’essi dal riferimento, abbiamo motivo di ri
tenere che le definizioni classiche di quantità di moto p mv ed energia cinetica
A
F
K 1 mv 2 debbano essere riformulate. Naturalmente, nel limite delle basse velocità,
2
le nuove formulazioni che stiamo cercando dovranno ridursi a quelle della teoria
classica, che già sappiamo essere corrette grazie ai numerosi esperimenti svolti in
questa regione sperimentale.
Come possiamo ricavare un’espressione per la quantità di moto relativistica?
Consideriamo una situazione dinamica specifica: un urto elastico (cioè in assenza di
qualsiasi attrito, e l’energia è conservata) tra le due sferette identiche A e B in figura,
che avanzano una verso l’altra con velocità uguali ed opposte, e sia m la loro massa.
Quando A e B non sono troppo veloci possiamo applicare la dinamica classica, i corpi hanno quantità di moto uguali in intensità ed opposte in verso, e quindi la quantità di moto complessiva risulta zero. Poiché la quantità di moto classica si deve conservare, dopo l’urto la quantità di moto complessiva sarà ancora zero. Scegliamo un sistema di riferimento S avente l’asse delle y lungo la direzione delle forze impulsive
15
-F
B
(cioè F e F in figura). Con questo termine intendiamo le intense forze repulsive
che agiscono durante un urto, e la cui direzione contiene il segmento che unisce i
centri delle due piccole sfere.
Che cosa comporta la conservazione della quantità di moto lungo l’asse x?
y
A
vAx
S
vAy
vAx
vAy
vBy
vBx
vBy
vBx B
x
Poiché non è presente l’attrito, non ci sono forze che agiscono perpendicolarmente
alle forze impulsive. Quindi, nel riferimento S scelto non ci sono forze lungo la direzione delle x , e non si osserva nessun cambiamento nelle velocità di entrambe le sferette lungo l’asse delle ascisse. La conservazione della quantità di moto nella direzione delle x richiede che px mvAx mvBx 0 rimanga nulla dopo l’urto come lo
e vBx
le componenti delle velocità dopo la colera prima di esso. Indicando con vAx
lisione:
prima dell ' urto abbiamo
dopo l ' urto deve essere
vAx vBx
pertanto
m vBx
0
m vAx
m vAx m vBx 0
vBx
pertanto vAx
Giacché la relazione vAx vBx rimane la stessa prima e dopo l’urto, e nessun cambiamento di direzione lungo le ascisse ha luogo, basta che le componenti x di entrambe le velocità rimangano immutate (vedi figura) per soddisfare la conservazione
della quantità di moto in direzione delle x :
vAx e vBx
vBx .
vAx
Che cosa comporta la conservazione della quantità di moto lungo l’asse y?
Nella direzione delle y , sul sistema delle due sferette nel loro complesso sta agendo
una forza risultante nulla (F F 0 in base alla terza legge della dinamica). Ma
sulla particella A agisce una forza F , che cambia il verso della componente y della
velocità. Un’analoga inversione si osserva nella componente y della velocità della
particella B, a causa dell’azione di F . Che possiamo dire dell’intensità di queste
componenti y che sono state invertite? La conservazione della quantità di moto nella
la direzione delle ordinate py mvAy mvBy 0 richiede che la quantità di moto
complessiva lungo y rimanga zero anche dopo l’urto, come lo era prima:
prima dell ' urto abbiamo
dopo l ' urto deve essere
vAy vBy
pertanto m vAy m vBy 0
m vBy
0
m vAy
vBy
pertanto vAy
La relazione vAy vBy è la stessa prima e dopo l’urto, così anche in questo caso
l’intensità delle componenti rimane inalterata. Ma le osservazioni mostrano
un’inversione delle velocità lungo la direzione delle y . Pertanto, per soddisfare la
legge della conservazione della quantità di moto lungo y , le componenti y di entrambe le velocità devono rimanere immutate in intensità ma cambiare di verso (vedi
figura).
vAy e vBy
vBy
vAy
Questo significa che l’asse delle ascisse è parallelo alla linea tratteggiata in figura,
rispetto alla quale le due traiettorie sono simmetriche. Questa simmetria comporta
che le due sferette s’incontrano a metà strada sia lungo la direzione x che lungo la
direzione y
16
y
Che cosa cambia a velocità relativistiche?
Adesso ci proponiamo di capire se la quantità di moto (nella sua forma classica
p mv ) si conserva anche quando A e B viaggiano a velocità relativistiche lungo
l’asse delle ascisse. Scegliamo però di osservare lo stesso urto da un riferimento S
nel quale la particella B ha una velocità nulla lungo le ascisse. Questo è possibile se
S si muove verso sinistra alla stessa velocità alla quale B avanza in S . Come si vede
in figura, uno sperimentatore in S vede:
A
relativistica! S
relativistica!
1) la particella B che si muove parallelamente alle y , e la sua componente non
B
x
relativistica di velocità vBy che viene invertita durante l’urto;
2) la particella A che ha una componente relativistica lungo x (la indicheremo
semplicemente con v ) che emerge immutata dall’urto, e una componente
non relativistica di velocità lungo y , che viene invertita dall’urto.
Tuttavia, mentre la componente y delle velocità di entrambe le particelle erano
uguali ed opposte in S , adesso in S non lo sono più. Infatti, a causa della presenza
di della componente relativistica v (posseduta da A ma non da B), uno sperimentato- y
re in S vede A soggetta al fenomeno della dilatazione temporale. Ora, poiché le
A
componenti y delle velocità sono non relativistiche, non c’è contrazione delle lunghezze in questa direzione (perpendicolare alla velocità relativistica). Pertanto, anche
in S le due sferette s’incontrano a metà strada lungo le y , attraversando uguali di-
S
v
vAy
vBy
stanze lungo le ordinate, esattamente come danno in S , ma A in un tempo più lungo
di un fattore rispetto a B. Dobbiamo concludere che, in S , A sta viaggiando lun-
B
x
go y con una velocità più lenta di un fattore rispetto a B, cioè:
vAy vBy /
Quindi la quantità di moto classica non è conservata in S perché, lungo l’asse y ,
l’urto inverte il moto di due particelle con la stessa massa ma differenti componenti
y della velocità. Infatti, come sappiamo, la semplice inversione delle velocità senza
cambio di intensità è possibile, in un urto elastico tra due sfere solo se collidono con
velocità uguali ed opposte. Facciamo qualche calcolo per verificare che la quantità di
moto classica non si conserva lungo y . Prima dell’urto abbiamo:
py mvAy mvBy m(vBy / vBy ) mvBy (1 1/ )
e dopo l’urto:
mvBy
m (vBy / vBy ) mvBy (1 1/ )
py mvAy
si ottiene così l’impossibile risultato py py al posto di quello atteso: py py .
p
Che cosa dobbiamo cambiare se vogliamo che la quantità di moto si conservi?
relativistica
Se vogliamo che la quantità di moto lungo la direzione y sia conservata in S , dob
biamo incrementare il valore di p per la particella A dello stesso fattore di cui la
sua velocità trasversa (cioè perpendicolare alle forze impulsive) è diminuita. La cor
retta espressione della quantità di moto relativistica non è quindi p mv , bensì:
mv
p mv
1 v 2 /c2
17
classica
c
v
È facile verificare che questa espressione relativistica per la quantità di moto soddisfa
la legge di conservazione lungo y . Poiché per B abbiamo 1 , considerato che le
vyA , vyB
vyB ) , e che inoltre
velocità sono invertite nella collisione (vyA
vyA vyB / , risulta:
py m vAy m 1 vBy m (vBy / vBy ) 0
m 1 vBy
m (vBy / vBy ) 0
py m vAy
Come si vede, la quantità di moto lungo le ordinate si conserva, essendo zero sia
prima sia dopo l’urto.
Qual è il legame con la quantità di moto classica?
mR
m assa
r e la tiv is ti c a
È facile riconoscere che quando v diviene trascurabile rispetto a c (e 1 ),
l’espressione relativistica per p si riduce alla sua forma classica. D’altra parte, a velocità
molto elevate, cioè quando v /c 1 , la quantità di moto relativistica tende a infinito. Ri
guardo alla formula p mv , molti fisici (specialmente nei primi anni dopo la scoperta
della teoria della relatività) preferiscono pensare alla massa di una particella puntiforme
come ad una quantità dipendente dalla velocità, e inglobare il fattore nella massa. In tal
modo si ottiene p mRv , dove mR m è detta massa relativistica, ed è una grandezza
m
c v
fisica che cresce con v (vedi figura). Tuttavia, in tempi più recenti sta prevalendo la tendenza a mantenere l’uso della massa newtoniana come proprietà invariante della materia. Questo perché non esiste un modo per misurare direttamente la massa di una particella in movimento, e ciò che può essere misurato è soltanto il cambiamento della sua
quantità di moto con la velocità. Tutt’e due le interpretazioni sono legittime, e anche Einstein, nel corso dei suoi studi cambiò idea al riguardo.
In che modo possiamo trovare un’espressione relativistica per l’energia cinetica?
L’energia cinetica K di una particella è il lavoro che occorre compiere su di essa per
portarla da ferma fino ad avere velocità v . A velocità non relativistiche l’energia ci-
F
x
netica di una particella è K 12 mv 2 . Cerchiamo ora un’espressione per K che valga
v
in meccanica relativistica. Consideriamo dunque una particella e calcoliamo
l’aumento K di energia cinetica prodotto dal lavoro di una forza F per un tratto
di lunghezza x . Per semplicità limitiamoci al caso in una sola dimensione (vedi
figura), in cui forza e spostamento sono paralleli ed equiversi:
K |F | |x | cos 0 F x
Inseriamo la seconda legge della dinamica nella forma F p /t :
v
v
v
v
variazione del prodotto
di due grandezze
(v ) v v
K
p
x
x m p
mvp mv (mv )
t
t
Dove x /t è la velocità media durante x , e supponiamo x così breve che non
cambia molto nel risultato finale se in questa particolare sostituzione la facciamo
coincidere con la velocità v all’inizio del tratto. Calcoliamo ora p , cioè di quanto
varia la quantità di moto quando v aumenta di v e cresce di . Ricordando
che p mv , e che la massa newtoniana m è invariante, si tratta di calcolare la variazione del prodotto delle due grandezze e v . La formula che adoperiamo
(mv ) m(v v) è dimostrata dal ragionamento in figura, dove si trascura il
quadratino in alto a destra, tanto più piccolo quanto più corto è x :
K mv(v v ) m(vv v 2 )
18
Come si vede la variazione di energia cinetica prodotta dal lavoro di F dipende sia
dalla variazione di v sia dalla variazione di (a sua volta dipendente da v ). Dalla
definizione di 1 / 1 v 2 /c 2 , elevando al quadrato otteniamo:
2c 2 2v 2 c 2
Calcoliamo ora di quanto variano ambo i membri di questa uguaglianza in conseguenza dell’aumento di v e . Considerato che c 2 è una costante, la sua variazione
è nulla, e inoltre ( 2c 2 ) 2c 2 (vedi figura la variazione di v 2 o di 2 ). Per la
variazione del prodotto delle due grandezze 2 e v 2 possiamo applicare ripetuta-
v
v v
v
v2
v v
v
v
mente la formula precedente:
( 2 v 2 ) 2 v 2 v 2 2 2 2v v v 2 2
Essendo la variazione del primo membro ( 2c 2 ) 2c 2 , risulta infine:
2
2
2
2c 2v v v 2
2
2
c vv v
Sostituendo l’espressione per c 2 in quella per K si ottiene:
K mc 2
Applichiamo questa formula fra lo stato iniziale in cui la particella è ferma e quello
in cui ha raggiunto velocità v :
K 0 mc 2 ( 0 )
Poiché quando la particella è ferma si ha 0 1 , arriviamo all’espressione per
l’energia cinetica in relatività:
Energia cinetica relativistica di una particella:
K mc 2 mc 2 ( 1)mc 2
Che cosa possiamo dire dell’energia totale di una particella libera in moto?
In meccanica classica, l’energia totale di una particella libera corrisponde alla sua
energia cinetica. Tuttavia, guardando l’espressione K mc 2 mc 2 , si nota che essa è nella forma di una differenza della stessa quantità mc 2 , prima calcolata a velocità v , e poi a velocità v 0 (e 1 ). Quest’idea suggerisce che l’energia di una
particella in moto può essere ottenuta sottraendo a un’energia totale a velocità v ,
E mc 2 , un’energia a riposo E 0 mc 2 , indipendente dalla velocità. Pertanto,
l’energia relativistica totale di una particella libera è:
vistica: E mRc 2
Energia relativistica totale di una particella libera
E K E 0 mc 2
Usando la massa relati-
mc 2
1 v 2 /c 2
K
relativistica
K ( 1)mc 2
Come si vede dal membro di destra di questa equazione, quando la particella è in
quiete ( v 0 , 1 ), l’energia totale uguaglia l’energia a riposo E E 0 mc 2 .
Quindi, una particella isolata possiede energia, anche se non si sta muovendo, per il
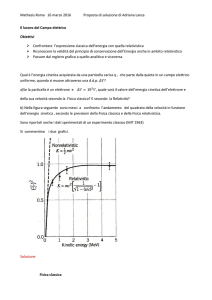
solo fatto di avere una massa. D’altra parte, l’energia di una particella tende a infinito quando v tende a c (e il denominatore diviene nullo). Di conseguenza, nessuna
particella materiale potrà mai raggiungere c , dato che le forze del mondo reale possono solo svolgere un quantitativo finito di lavoro su di essa, e nessun quantitativo
19
classica
K 1 mv 2
2
c
v
finito di lavoro è in grado di fornire una quantità di energia infinita. Inoltre, come si
vede dal grafico di v in funzione dell’energia cinetica K ( 1)mc 2 , a mano a
v
mano che v si avvicina a c , sono necessari incrementi di energia cinetica progressivamente più grandi ( K 2 K1 ) per accelerare la particella incrementandone la
c
v
velocità della stessa v . In ogni caso, la formula E 0 mc 2 che associa la massa
v
all’energia di riposo è una legge della fisica, e non un teorema che può essere dimostrato partendo da altre leggi, quindi la sua conferma ultima sono le osservazioni
sperimentali.
K 1
K 2
K
In che senso possiamo dire che massa ed energia sono equivalenti?
Il significato della formula per l’energia a riposo E 0 mc 2 viene tutt’oggi dibattuto
in letteratura scientifica. Significa che la massa e l’energia sono la stessa grandezza fisica
oppure che sono semplicemente proporzionali fra loro? Sperimentalmente è stato osservato numerose volte che le particelle dotate di massa, come ad esempio gli elettroni oi positroni (elettroni con carica positiva) quando collidono, possono essere trasformate in radiazione elettromagnetica (che è priva di massa). Perciò è possibile
convertire l’energia in massa e la massa in energia. Questo significa che possiamo
misurare l’energia adoperando l’unità di misura della massa, e la massa adoperando
le unità di misura dell’energia, come se fossero due aspetti di un’unica grandezza
radiazione
elettomagnetica
fisica, la massa-energia, (proprio come un secolo e mezzo fa sono state unificati i joules
e le calorie). Possiamo fare un esempio calcolando l’energia a riposo corrispondente
alla massa di m 1 kg :
positrone
elettrone
E 0 mc 2 1 kg (3 10 8 m/s)2 9 1016 J
In fisica delle particelle, poiché le masse e le energie coinvolte sono molto più piccole
di quelle tipiche della scala degli oggetti, si utilizza una unità di misura molto più
piccola del joule, chiamata mega elettron-volt: 1 MeV 1.602 1013 J . Quindi, per
l’energia a riposo di un elettrone e di un protone abbiamo:
E 0e mec 2 (9.109 1031 kg) (2.998 108 m/s)2 /(1.602 1013 J /MeV) 0.511 MeV
E 0 p mpc 2 (1.672 1027 kg) (2.998 108 m/s)2 / (1.602 1013 J /MeV) 938 MeV
Allo scopo di evitare la divisione per c2 , la massa è spesso data in unità MeV/c 2 :
me 9.11 1031 kg 0.511 MeV/c 2
m p 1.67 1027 kg 938 MeV/c 2
20