Note sul pendolo
Maurizio Loreti
Dipartimento di Fisica
Università degli Studi di Padova
Ultima revisione: 5 gennaio 2006
∗
Fu allora che vidi il Pendolo. La sfera,
mobile all’estremità di un lungo filo fissato alla volta del coro,
descriveva le sue ampie oscillazioni con isocrona maestà.
Umberto Eco, Il pendolo di Foucault
1 Il pendolo semplice
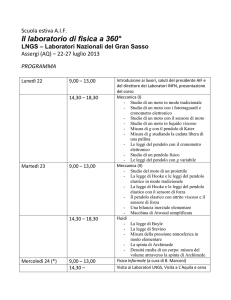
Un pendolo semplice (si faccia riferimento alla figura 1) consiste in un punto materiale P
di massa m, fissato ad una estremità di un filo ideale1 di lunghezza l il cui altro estremo è
vincolato a trovarsi nel punto O. Il pendolo oscilla tra i due punti della traiettoria circolare
π
di centro O e raggio l che corrispondono all’elongazione massima α (con 0 < α < 2 ):
ovvero, nel riferimento polare con origine O ed asse OX, tra il punto G di coordinate
(l, −α) ed il punto G′ di coordinate (l, +α). Sia poi ϑ la coordinata angolare di P in un
generico istante (−α ≤ ϑ ≤ α), ed indichiamo con
ω=
dϑ
dt
dω
d2 ϑ
=
dt
dt 2
e
la sua velocità angolare e la sua accelerazione angolare rispettivamente; a P è associato un
vettore velocità avente in ogni istante direzione tangente alla traiettoria e modulo v = ωl.
L’equazione del moto del pendolo semplice si trova imponendo che il momento (rispetto ad O) delle forze applicate sia uguale alla derivata rispetto al tempo del momento
(sempre rispetto ad O) della quantità di moto:
d OP ∧ T + mg =
OP ∧ mv
dt
(1)
Col simbolo T abbiamo indicato la tensione del filo, che è diretta lungo OP ed ha dunque momento nullo rispetto ad O; nella configurazione descritta dalla figura 1 il momento delle forze agenti è diretto normalmente al piano di figura, ha verso che si avvicina
all’osservatore e modulo mgl sin ϑ.
La velocità v del pendolo è sempre perpendicolare ad OP: quindi il momento della
quantità di moto ha modulo mvl = ml2 ω e direzione perpendicolare al piano di figura,
1 Ovvero
inestensibile, privo di massa e perfettamente flessibile.
1
O
α
ϑ
l
l cos α
T
G
G’
P
mg
X
Figura 1: schema di pendolo semplice; α rappresenta l’elongazione massima, e ϑ quella
generica.
2
mentre il verso della sua derivata è diretto lontano dall’osservatore. Per meglio chiarire
questo punto, basta osservare che a valori positivi di α (e quindi di sin α) corrispondono o
velocità angolari positive e di modulo decrescente, o velocità angolari negative e di modulo
crescente — e quindi accelerazioni angolari in ogni caso negative; mentre per sin α < 0 le
accelerazioni angolari sono sempre positive.
In definitiva, sostituendo nella (1) queste espressioni, si ricava l’equazione del moto
del pendolo
g
d2 ϑ
+ sin ϑ = 0
2
dt
l
(2)
2 Le piccole oscillazioni
Un’equazione differenziale del tipo
d2 x
+ ω2 x = 0
dt 2
(3)
(con ω costante positiva2 ) è nota nell’analisi come equazione differenziale del moto armonico; la soluzione generale della (3) è infatti del tipo
x(t) = A · sin(ωt + ϕ)
(4)
e dipende da due costanti di integrazione: A (ampiezza massima) e ϕ (fase iniziale). La
(4) corrisponde ovviamente ad un moto periodico di periodo
T =
2π
ω
Nel limite delle piccole oscillazioni (ossia quando sin ϑ ≈ ϑ), la (2) si riduce alla (3)
ponendo
g
ω2 =
l
e, se l’approssimazione si può ritenere valida, il moto del pendolo semplice è quindi un
moto armonico di periodo
s
l
T0 = 2π
(5)
g
Il fatto che nella (5) non compaia α si esprime affermando che le piccole oscillazioni del
pendolo sono isocrone; osserviamo anche che il periodo è indipendente dalla massa del
pendolo. Se (quando t = 0) il pendolo si trova sull’asse polare diretto verso la regione
degli angoli positivi, l’equazione del moto che si ottiene dalla (4) tenendo conto di queste
condizioni al contorno è la ϑ(t) = α sin(ωt).
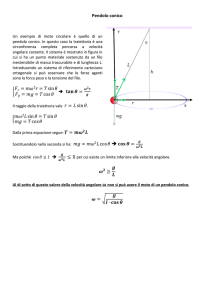
3 Il pendolo composto
Per pendolo composto si intende semplicemente un corpo rigido vincolato a ruotare
attorno ad un asse fisso, non verticale e non passante per il suo baricentro; l’equazione
2ω
è detta anche pulsazione del moto.
3
O
ϑ
h
G
mg
X
Figura 2: schema di pendolo composto; G è il baricentro del corpo.
del moto di questo sistema fisico (vedi la figura 2) viene ancora ricavata calcolando il momento (rispetto all’asse fisso) delle forze applicate ed uguagliandolo alla derivata rispetto
al tempo del momento della quantità di moto: quest’ultimo viene infine espresso come
il prodotto Iω del momento d’inerzia (rispetto all’asse fisso) per la velocità angolare del
corpo.
Agendo analogamente a quanto fatto per il pendolo semplice, si giunge facilmente alla
mgh
d2 ϑ
+
sin ϑ = 0
2
dt
I
(h è la distanza OG tra l’asse di sospensione ed il baricentro); e, nel limite delle piccole
oscillazioni, il moto è ancora periodico con un periodo T0 dato dalla
s
I
T0 = 2π
mgh
che si riduce formalmente alla espressione (5), già vista per il pendolo semplice, una volta
definita la costante l attraverso la
I
l=
mh
Questa costante (che dimensionalmente equivale a una lunghezza) si chiama lunghezza
ridotta del pendolo composto: è quella che dovrebbe avere un ipotetico pendolo semplice
che oscillasse con lo stesso periodo di quello composto studiato.
Visto che le equazioni del moto del pendolo composto e di quello semplice sono
identiche, quanto in seguito diremo a proposito del secondo si applica anche al primo.
4
4 L’isocronia delle oscillazioni
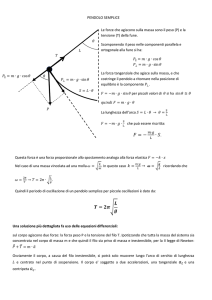
Riprendiamo il pendolo semplice, e vediamo cosa si può dire se non si vuole usare
l’approssimazione delle piccole oscillazioni. Osserviamo per cominciare che, se il pendolo
semplice ha un periodo T dipendente da α, la funzione T (α) deve contenere soltanto potenze pari dell’elongazione massima: dovendosi avere ovviamente due moti con lo stesso
periodo quando si cambia α in −α.
In realtà per trovare il periodo del pendolo conviene non tanto tentare di risolvere
l’equazione del moto (2) quanto piuttosto applicare il principio di conservazione dell’energia: la somma dell’energia cinetica K e di quella potenziale V del pendolo deve essere
costante in ogni istante, ed in particolare
dϑ 2
1
ml2
− 0 = V (α) − V (ϑ) = mgl (cos ϑ − cos α)
K(ϑ) − K(α) =
2
dt
(si è scelta come quota di riferimento per l’energia potenziale quella di O);
dϑ
dt
2
=
2g
(cos ϑ − cos α)
l
(6)
Dalla (6) si ottiene, volendo, l’equazione del moto (2) derivando entrambi i membri rispetto
a t; o, per quel che ci interessa ora, si può giungere alla
s
dϑ
2g
=
(cos ϑ − cos α)
dt
l
ed infine alla
2π
dϑ
=
dt
T0
q
2(cos ϑ − cos α)
(7)
indicando con T0 il periodo delle piccole oscillazioni, che abbiamo già ricavato e che è
dato dalla formula (5). Separando le variabili, l’equazione (7) diventa
dt =
T0
p
dϑ
2π 2(cos ϑ − cos α)
ed integrando (tenendo conto che per spostarsi da ϑ = 0 a ϑ = α il pendolo impiega un
quarto di periodo; notiamo incidentalmente che in questo intervallo di integrazione ϑ è
limitato al primo quadrante) giungiamo alla
Z
T
4
0
dt =
T
T0
=
4
2π
Zα
0
ed infine alla
T =
dϑ
p
2(cos ϑ − cos α)
2T0
I
π
(8)
ove per semplicità si è indicato con I il valore dell’integrale definito
I=
Zα
0
dϑ
p
2(cos ϑ − cos α)
5
(9)
Per calcolare I cominciamo dapprima a cambiare variabili, esprimendo il coseno sia di
ϑ che di α mediante le formule di bisezione
cos ϑ = 1 − 2 sin2
ϑ
2
cos α = 1 − 2 sin2
e
α
2
(10)
sfruttando le quali la (9) può essere scritta
I=
1
2
Zα
0
dϑ
q
sin2
α
2
− sin2
ϑ
2
o anche, introducendo per semplicità la costante k = sin
I=
1
2
Zα
0
dϑ
q
k2 − sin2
α
2
(con 0 < k < 1),
ϑ
2
Cambiamo poi variabile di integrazione, passando dalla ϑ alla
ϑ
ϑ
sin 2
sin 2
= arcsin
ϕ = ϕ(ϑ) = arcsin
sin α
k
2
Per eseguire la sostituzione, calcoliamo
ϕ(0) = 0
ϕ(α) =
e
π
2
(dunque ϕ appartiene al primo quadrante del cerchio trigonometrico, e di conseguenza
risulta 0 < cos ϕ < 1); ed inoltre abbiamo:
sin
ϑ
cos
=
2
k2 − sin2
ϑ
= k sin ϕ
2
s
1 − sin2
ϑ
=
2
(11)
q
1 − k2 sin2 ϕ
ϑ
= k2 1 − sin2 ϕ = k2 cos2 ϕ
2
Differenziando la (11) otteniamo
1
ϑ
cos dϑ = k cos ϕ dϕ
2
2
da cui ricaviamo la relazione tra dϑ e dϕ
dϑ =
2k cos ϕ
cos ϑ2
e insomma, operando la sostituzione:
I =
1
2
Z
π
2
0
2k cos ϕ
dϕ = q
dϕ
1 − k2 sin2 ϕ
1
2k cos ϕ
q
dϕ =
k cos ϕ 1 − k2 sin2 ϕ
6
Zπ
2
0
f (ϕ; x) dϕ
(12)
ove si è posto sia x = k2 che
− 1
2
f (ϕ; x) = 1 − x sin2 ϕ
(13)
A questo punto, per calcolare il valore della (12) non resta che sviluppare in serie di
McLaurin la f , definita nell’equazione (13), nell’intorno di x = 0: le derivate prima e
seconda (rispetto alla x) valgono
3
f ′ (ϕ; x) =
−
1
d
2
sin2 ϕ
f (ϕ; x) =
1 − x sin2 ϕ
dx
2
f ′′ (ϕ; x) =
− 5
d2
3
2
sin4 ϕ
1 − x sin2 ϕ
f (ϕ; x) =
2
dx
4
e
quindi il loro valore per x = 0 è
f ′ (ϕ; 0) =
1
sin2 ϕ
2
f ′′ (ϕ; 0) =
3
sin4 ϕ
4
e
e lo sviluppo della (13) vale
f (ϕ; x) = 1 +
1
3
x sin2 ϕ + x 2 sin4 ϕ + O(x 3 )
2
8
f (ϕ; k) = 1 +
3
1 2
k sin2 ϕ + k4 sin4 ϕ + O(k6 )
2
8
ossia
Tornando all’integrale definito (12),
I=
Z
π
2
dϕ +
0
= I1 +
1 2
k
2
Z
π
2
sin2 ϕ dϕ +
0
3 4
k
8
Z
1 2
3
k I2 + k4 I3 + O(k6 )
2
8
π
2
sin4 ϕ dϕ + O(k6 )
0
(14)
indicando con
π
2
I1 =
Z
I2 =
Zπ
dϕ =
0
2
π
2
sin2 ϕ dϕ
0
7
(15)
e
Zπ
2
I3 =
sin4 ϕ dϕ
(16)
0
gli integrali definiti dei primi termini dello sviluppo. Per calcolare l’integrale (15) sfruttiamo la relazione
sin2 ϕ =
1 − cos(2ϕ)
2
e sostituiamo la nuova variabile t = 2ϕ (con dt = 2 dϕ):
I2 =
Z
π
2
sin2 ϕ dϕ =
0
Zπ
0
1
1 − cos t dt
=
2
2
4
Zπ
π o
π
1 n π (1 − cos t) dt =
t 0 − sin t 0 =
4
4
0
Per calcolare invece l’integrale (16), sfruttiamo (sempre sostituendo t = 2ϕ) la
sin4 ϕ =
1 − cos t
2
2
=
1 − 2 cos t + cos2 t
4
da cui si ricava
Zπ
2
I3 =
sin4 ϕ dϕ =
0
Zπ
0
1 − 2 cos t + cos2 t dt
1
=
4
2
8
Zπ
dt −
0
1
4
Zπ
cos t dt +
0
1
8
Zπ
cos2 t dt
0
e, sostituendo ancora u = 2t nell’ultimo termine, essendo
cos2 t =
1 − cos u
1 − cos(2t)
=
2
2
e
dt =
du
2
si trova
Z
π 1 2π 1 − cos u du
1
π
−
sin t 0 +
8
4
8 0
2
2
n
o
2π
π
1 2π =
u 0 − sin u 0
+
8
32
I3 =
=
π
3
π
+
=
π
8
16
16
Sostituendo i valori dei tre integrali definiti nella (14), ed il valore di I così ricavato
nella (8), si ottiene dapprima
I =
π 2
9
π
+
k +
π k4 + O(k6 )
2
8
128
e poi
T = T0
2
9 4
1
I = T0 1 + k2 +
k + O(k6 )
π
4
64
(17)
L’ultimo passo consiste nell’esprimere la (17) in funzione di α, tenendo conto che α è
piccolo e considerando i contributi dei termini fino ad α4 ; partendo dal noto sviluppo di
sin(x) in serie di McLaurin
x3
sin(x) = x −
+ O(x 5 )
3!
8
ricaviamo dapprima
#2
α
α3
α2
α4
5
−
+ O(α ) =
−
+ O(α6 )
2
48
4
48
"
#4
α
α3
α4
4 α
4
5
k = sin
=
−
+ O(α )
=
+ O(α6 )
2
2
48
16
α
=
k = sin
2
2
2
"
e, sostituendo queste espressioni nella (17), si ottiene
1 2
1
9
T = T0 1 +
α −
α4 +
α4 + O(α6 )
16
192
1024
ed infine
1 2
11
T = T0 1 +
α +
α4 + O(α6 )
16
3072
(18)
11
In quest’ultima formula, il rapporto tra il termine in α4 e quello in α2 vale 192 α2 ;
tale rapporto è inferiore al 10% quando α ≲ 1.32 rad ≈ 76◦ , ed inferiore all’1% quando
α ≲ 0.42 rad ≈ 24◦ . Trascurando i termini dell’ordine di α4 si introduce un errore relativo
che è dato, a meno di termini O(α6 ), da
∆T
11
=
α4
T0
3072
e che è inferiore all’1% già per oscillazioni di elongazione α ≲ 1.29 rad ≈ 74◦ .
Nella normale tecnica di laboratorio si scelgono elongazioni massime dell’ordine dei
10◦ ≈ 0.17 rad: per le quali, trascurando il termine O(α4 ), l’errore relativo introdotto è
.
circa 3×10−6 (una parte su 300 000); mentre, trascurando anche i termini O(α2 ) ed usando
la formula (5) delle piccole oscillazioni, l’errore relativo (che vale, a meno di termini O(α4 ),
α2
) sarebbe approssimativamente 2 × 10−3 (una parte su 500).
16
Concludendo, la formula che si ottiene dalla (18) trascurando i termini di ordine superiore a quello in α2 :
!
α2
T = T0 1 +
16
si può ritenere esatta per le esperienze normalmente eseguite nel laboratorio.
5 L’usura del coltello
Una differente causa di errore sistematico è l’usura del coltello di acciaio temprato
mediante il quale viene realizzata la sospensione del pendolo, e che appoggia su una
superficie piana anch’essa di acciaio temprato; per l’inevitabile consumarsi del metallo, il
coltello non è infatti un diedro perfetto: ma la sua parte terminale (si veda la figura 3)
può essere approssimata con una superficie cilindrica di raggio r che, per gli strumenti a
disposizione nel laboratorio, è dell’ordine dei 5 × 10−2 mm.
Per questo motivo il moto reale del pendolo (si veda la figura 4) non è una rotazione
attorno ad un asse passante per il punto più basso del coltello, indicato con A sia in figura
9
O
r
S
A
S
Figura 3: a sinistra, una rappresentazione schematica del coltello mediante il quale è
realizzata la sospensione dei pendoli; a destra, il dettaglio.
3 che in figura 4; ma si può pensare che la superficie cilindrica di contatto tra il coltello
ed il piano di appoggio SS rotoli senza strisciare attorno alla retta per R normale al piano
della figura 4, retta la cui posizione cambia di istante in istante durante il moto. Durante le
oscillazioni del pendolo il centro di curvatura del coltello, O, rimane costantemente sulla
superficie piana TT parallela a quella d’appoggio SS e ad una distanza r da essa.
Per complicare ulteriormente le cose, tutte le distanze misurate nel laboratorio sono
riferite all’estremità terminale A del coltello e non al suo centro di curvatura; per cui, se G
è il baricentro del pendolo, con h si deve intendere la distanza AG.
Per cominciare, nel moto reale del pendolo il momento d’inerzia andrebbe calcolato
rispetto all’asse di rotazione istantanea passante per R; e varrebbe quindi
IR = IG + m · GR
2
(19)
(usando il teorema di Steiner-Huygens, ed indicando con IG il momento d’inerzia rispetto
ad una retta per G normale al piano della figura 4).
Il teorema del coseno ci permette di scrivere
GR
2
2
2
= GO + OR − 2GO · OR · cos ϑ = (r + h)2 + r 2 − 2r (r + h) cos ϑ
10
(20)
T
T
O
ϑ
r
r
A
S
S
R
G
Figura 4: l’effettivo moto di rotolamento del coltello sul piano di appoggio.
11
e, sfruttando la formula di bisezione (10) per esprimere l’angolo ϑ, la (20) diventa
ϑ
2
GR = (r + h)2 + r 2 − 2r (r + h) 1 − 2 sin2
2
2
ϑ
= (r + h) − r + 4r (r + h) sin2
2
= h2 + 4r (r + h) sin2
ϑ
2
per cui IR vale, sostituendo nella (19):
IR = IG + mh2 + 4mr (r + h) sin2
ϑ
ϑ
= IA + 4mr (r + h) sin2
2
2
(21)
La differenza tra IR ed IA è in pratica trascurabile, perché sia r che ϑ sono piccoli:
essendo h ∼ 103 mm, approssimando (r +h) con h e supponendo che sia ϑ ∼ 10◦ , l’ultimo
.
termine della (21) è più piccolo di mh2 per un fattore 2 × 10−6 (una parte su 660 000): per
cui il confondere IR con IA non comporta in realtà alcun errore apprezzabile. Dove invece
l’usura dei coltelli introduce una significativa deviazione dal comportamento ideale è nel
calcolo dell’energia potenziale da usare nella (6): infatti, usando come quota di riferimento
per l’energia potenziale quella del piano TT, la (6) diventa
1
Iω2 − mg(r + h) cos ϑ = cost.
2
(ove I = IR ≈ IA ) e, ricavando il periodo delle piccole oscillazioni, questo varrebbe in realtà
s
s
I
h
T = 2π
= T0
mg(h + r )
h+r
Tenendo conto che risulta r ≪ h, sviluppando il fattore di correzione in serie di McLaurin
e fermandoci al primo termine3 :
s
h
f (r ) =
=⇒
f (0) = 1
h+r
s
h+r
h
1
1
′
· −
f (r ) =
=⇒
f ′ (0) = −
2
h
(h + r )2
2h
per cui, in definitiva,
f (r ) =
s
h
r
≈ f (0) + f ′ (0) · r = 1 −
h+r
2h
(22)
e, con i valori dati per r ed h, l’errore sistematico sul periodo è dell’ordine di 2.5 × 10−5
.
(una parte su 40 000).
3 Sul
libro di testo è riportata una formula simile, ottenuta sviluppando invece
12
1
h+r
≈
1
h
−
r
h2
=
1
h
1−
r
h
.
6 La spinta di Archimede
Se il pendolo è fatto oscillare in aria, c’è un’ulteriore causa di errore sistematico: infatti
la (1) deve essere modificata per tener conto del fatto che, oltre alla forza peso, agisce
sul pendolo anche la spinta di Archimede. In pratica tutto avviene come se la massa
del pendolo fosse leggermente più piccola (nel termine che esprime il momento delle
forze agenti; in quello relativo al momento della quantità di moto non bisogna ovviamente
effettuare alcuna correzione).
Tenendo conto di questo, l’equazione del moto si deve scrivere (indicando con ρ e V
densità e volume del pendolo, e con ρa la densità dell’aria):
ρV · l2
dω
+ (ρ − ρa )V · gl sin ϑ = 0
dt
ρ − ρa g
d2 ϑ
+
sin ϑ = 0
dt 2
ρ
l
ed il periodo effettivo delle piccole oscillazioni è, rispetto al valore teorico T0 definito nella
(5), dato invece dalla
T = T0
s
ρ
ρ − ρa
o, approssimativamente (usando lo stesso sviluppo della (22), essendo ρa ≪ ρ):
T ≈ T0
ρa
1+
2ρ
!
(23)
Essendo ρa ≈ 1.2 × 10−3 gr/cm2 e ρ ≈ 7.9 gr/cm2 , la correzione è dell’ordine di 8 × 10−5
.
(una parte su 13 000).
7 Altre cause di errori sistematici
Altri effetti sistematici esistono, ma sono difficilmente quantificabili per via esclusivamente teorica. Ad esempio, quando venne effettivamente misurato il periodo dello
stesso pendolo in aria e sotto vuoto, la differenza risultò circa doppia di quanto previsto dalla (23); per spiegare questa discrepanza, Bessel la attribuì alla mancata considerazione degli attriti viscosi: che è ovviamente necessaria per descrivere completamente il
comportamento del sistema nell’aria.
Supponendo che il moto del pendolo avvenga in regime laminare, da una parte l’attrito
viscoso si oppone al moto e diminuisce il momento delle forze applicate; dall’altra gli
straterelli d’aria più prossimi al pendolo si muovono alla sua stessa velocità, e quelli
adiacenti hanno velocità via via decrescenti man mano che ce ne allontaniamo: per cui
massa e velocità di questi straterelli andrebbe considerata nel calcolo della quantità di
moto.
Questa analisi teorica è troppo complessa per essere svolta, ma l’esperimento su menzionato mostra empiricamente che questi effetti sono dello stesso ordine di grandezza di
quello attribuibile alla spinta di Archimede.
13