Beni Pubblici
NON RIVALITA’:
L’uso del bene da parte di un individuo non ne
ostacola l’uso da parte di altri individui.
(es. segnaletica stradale, faro, aeroporto….)
NON ESCLUDIBILITA’:
Dopo che il bene è fornito,
impedire che altri agenti ne beneficino.
(es. Segnaletica stradale, spiagge pubbliche, radio)
non si può
Tipi di beni
Beni pubblici puri (perfettamente non rivali ed escludibili)
beni privati (rivali ed escludibili)
Categorie intermedie dette beni pubblici impuri, parzialmente rivali ed
1
escludibili.
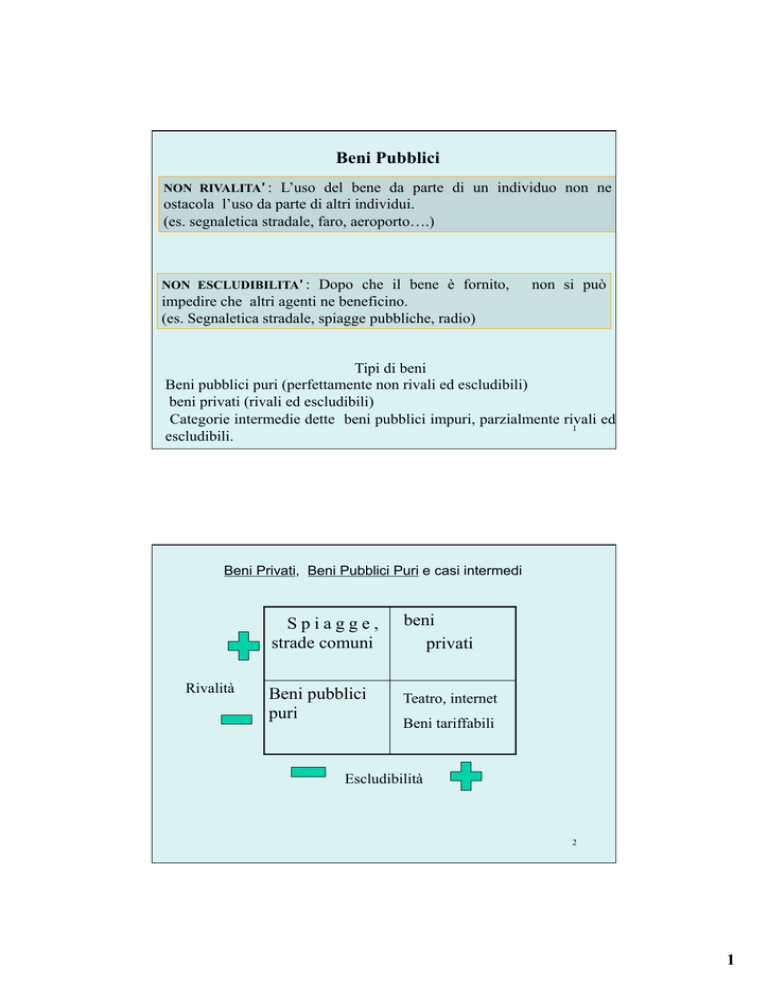
Beni Privati, Beni Pubblici Puri e casi intermedi
Rivalità
Spiagge,
strade comuni
beni
privati
Beni pubblici
puri
Teatro, internet
Beni tariffabili
Escludibilità
2
1
Discussione
Anche se tutti consumano la stessa quantità di un bene pubblico, ciò non
implica che tale quantità debba essere valutata da tutti gli agenti allo
stesso modo (per esempio il valore attribuito alla TV pubblica dipende
dalle preferenze degli utenti).
La caratteristica di bene pubblico dipende dalla tecnologia (es. TV) .
Beni privati o pubblici impuri possono essere forniti dal settore
pubblico (es. edilizia popolare, assistenza sanitaria).
• Beni pubblici (puri o impuri) possono essere forniti dal settore
pubblico ma prodotti dal settore privato (es. nettezza urbana,
infrastrutture).
• Beni pubblici possono essere forniti dal settore privato o
Congiuntamente col settore pubblico (es. istruzione, sicurezza…).3
Domanda di MKT di beni privati
La curva di domanda individuale misura la quantità di bene che si
domanda ad ogni prezzo o equivalentemente il beneficio marginale
privato del consumo del bene.
Per Agente A, dato il consumo di 1
unità, il valore di un incremento
marginale del consumo bene è p1*=5
Ad un prezzo di 5, la domanda di
mkt sarà 5, ovvero la somma
4
orizzontale delle dom- individuali
2
Domanda di Beni Pubblici (Somma Verticale)
PA+B = PA + PPB
PA+B*
Dato che i due consumatri condividono l’uso
del bene, il beneficio marginale sociale data la
quantità x* eguaglia la somma dei benefici
privati
PB*
Domanda aggregata A+B
P A*
DA+B
DA
DB
x*
0
x
5
Efficienza nella fornitura di Beni in equilibrio parziale.
Bene Pubblico
Bene Privato
S
DA+B
S
PA+B*
PB*
P*
DA+B
DA
0
xA* xB*
PPA*
DPA
DB
xA+B*
CM = p = BMA = BMB
0
DB
x*
CM = p = BMA + BMB
xP*
6
3
Beneficio Marginale e preferenze quasi-lineari
Propensione marginale a pagare (willingness to pay) per una ulteriore unità di bene
Supponiamo che il bene 2 sia utilizzato
come numerario (es. moneta, p2=1)
WTPp= p = SMS12.
UMi(x): Utilità marginale del bene i
SMS p2 =
x2
UM p (x)
UM 2 (x)
Se le preferenze sono quasi-lineari
l’utilità marginale del bene numerario è
costante U(Xp,X2) =U(Xp)+X2
0
xp*
Se le preferenze sono quasi-lineari
la
quantità scelta del bene pubblico non
7
dipende dal reddito
WTP1 = SMS12.
Fornitura efficiente di beni pubblici: Equilibrio Generale
Data la quantità di bene pubblico xp*, se l’agente 1 è sulla curva d’indifferenza
U1 , per l’agente 2 rimane la quantità di bene privato x2*.
Chamiamo VR2 il “vincolo delle risorse per l’agente 2”, costruito come la
differenza verticale fra la frontiera produttiva e la curva di indifferenza U1.
Trattandosi di un’identità
VR2 = SMTP2 - SMSP21.
VR2’ = SMTP2 - SMSP21.
x22
x12
x2*
Per massimizzare U2
VR2’ =SMSP22 cond. efficienza:
SMSP22 = SMTP2 - SMSP21.
U2
U1
xp*
xp
xp*
xp
8
4
Condizione di Ottimo per Scambio e PDZ (2 agenti):
SMSP21 + SMSP22 = SMTP2
In presenza di i=1,..,n agenti e se 2 è il bene numerario
∑i BMPi
= ∑i SMSP2i = SMTP2
Efficienza per produzione e scambio, economia con
n agenti i=1,..,n, e m beni privati j = 1,2,….m.
COND. DI SAMUELSON:
∑i SMSPji = SMTPj.
9
Fornitura efficiente di beni pubblici: aspetti distributivi
VR2 il “vincolo delle risorse per l’agente 2”, costruito come la differenza
verticale fra la frontiera produttiva e la curva di indifferenza U1, cambierà a
seconda dl livello di utilità scelto per 1. Poiché il livello di utilità raggiungibile da
1 dipende dal reddito, anche la fornitura efficiente di BP dipenderà in ultima
analisi dalla distribuzione del reddito e delle preferenze.
La distribuzione del reddito diventa irrilevante sulla quantità efficiente quando le
preferenze sono quasi-lineari.
x22
x12
U’1
U2
U1
xp
U’2
Xp*’ xp*
xp
10
5
Fornitura efficiente di beni pubblici in Equilibrio
Generale secondo Lindahl
Ci si chiede sotto quali ipotesi il settore privato
garantisce una fornitura efficiente di beni pubblici
Lindhal (1919) osservando che la valutazione marginale del bene pubblico è diversa
fra gli agenti, deduce che un sistema di prezzi “ad personam” può garantire livelli
efficienti di fornitura.
pi :prezzo personalizzato per l’agente i per il bene pubblico
Una fornitura efficiente richiede che Il costo c
dell’unità marginale di bene pubblico deve
essere coperto dai contributi individuali
∑i pi = c.
Meccanismo di Lindahl: Sistema di MKT che determina il prezzi Pk di ogni
bene pubblico k sulla base di contributi (tasse) personali pik di ogni agente i . In
equilibrio, Pk = ∑i pik = ck.
Prezzi finali e contributi individuali sono proposti da un banditore in modo che
Pk aumenta se c’è eccesso domanda aggregata di bene k e pi è maggiore per11gli
agenti con più alta valutazione marginale del bene pubblico.
Proprietà dell’equilibrio di Lindhal
Se l’equilibrio di Lindahl esiste è Pareto Efficiente,
quindi il mercato genera un outcome efficiente anche in
presenza di beni pubblici, in linea col I° teorema dell’economia
del benessere.
– Eq. MKT con beni privati: 1 prezzo unico per tutti; dom.
differenti
– Eq. LINDHAL con BP: Quantità unica per tutti, prezzi
personalizzati
Non è detto che l’equilibrio di Lindahl esista.
Si tratta di un equilibrio con contribuzione volontaria
Per sua natura soggetto a due tipi di difficoltà
12
6
I° Problema: rilevamento e aggregazione delle informazioni
•
Per generare un risultato efficiente i consumatori devono rivelare la loro WTP per il
bene pubblico dichiarando la quantità che realmente desiderano.
•
Ammettendo che siano sinceri, per ogni prezzo dichiareranno la propria quantità
ottimale, senza tener conto dei benefici altrui.
Se non c’è un corretto rilevamento e aggregazione delle informazioni sui SMS, c’è subfornitura. Ruolo del “banditore”
Es: pollici di uno schermo TV. Due studenti. si comprerà solo una delle 2 TV. Se
funziona l’equilibrio contributivo, si sommano le “offerte” di entrambi e si compra una
TV + grande.
•
•
S
DA+B
PA+B*
PB*
PPA*
*
DPADBx
II° problema: interazione strategica, Free-riding
Data la non escludibilità, in condizioni di interazione strategica gli agenti
preferiranno dichiarare una domanda del bene pubblico inferiore a quella vera
per contribuire meno al suo finanziamento, sfruttandone ugualmente la fornitura
a spese altrui.
Non contr. è la strategia
dominante per entrambi
Utente 2
contribuisce
Utente 1
evade Contrib.
Esempio:
Fornitura di un bene pubblico,
al costo C .
2 consumatori, con V1 <V2 < C.
Il costo di pdz è diviso tra i due
utenti, ognuno paga C/2
evade
V1 – C/2;
V2 – C/2
V1 – C
V2
V1
V1 – C
0
Risultato: il bene non è fornito anche se V1+V2
> C. Inefficienza!
7
Rivelazione preferenze su beni pubblici (Clarke Tax)
E’ possibile creare meccanismi capaci di far rivelare agli agenti le loro
vere preferenze. Esaminiamo la Clarke tax, ispirata dalle aste al
secondo prezzo.
Si sceglie se fornire un bene pubblico a n agenti. Il costo complessivo è
C e la quota individuale da pagare è quindi C/n.
Ogni agente dichiara la propria valutazione Vn.
Se Σ(Vn-C/n)>0 il bene viene fornito.
Chiamiamo vi =Vi -C/n la valutazione netta di i.
Un agente risulta decisivo o pivotale quando dichiarando il
valore attribuito al bene sovverte la decisione di fornire (non
fornire) il bene ottenuta aggregando le dichiarazioni degli altri
agenti
15
Regola di Clarke-Groves + esempio
Clarke Tax. Ogni agente i contribuisce al bene (se fornito) pagando
solo la sua quota C/n se non è decisivo mentre se è decisivo paga una
tassa Ti = valore assoluto di
∑j ≠ i vj *
• Applicando questa regola dichiarare la propria vera valutazione è
una strategia dominante per tutti i giocatori.
• Dimostriamo questo risultato con l’esempio di 3 coinquilini che
ricevono in regalo una vecchia radio. La scelta è: tenerla o no.
• Non costa nulla acquistarla quindi consideriamo direttamente le
valutazioni nette pari a : v1=v2 = -50, v3=150
16
8
Scelta di 3
-150
0
150
•
•
Dichiarare sinceramente la propria valutazione è una strategia dominante
è per ogni dichiarazione altrui, v3 =150 non è dominata da altre strategie e in certi casi è
strettamente dominante.
• Consideriamo tutti i possibili casi (dato che 3 non sa cosa dichiareranno 1 e 2)
1) v1+v2 < - 150
• Se 3 dichiara 150 o meno di 150 il bene non è fornito, quindi 150 non è dominata da v3 <
150.
• Se 3 dichiara + di 150, o il bene non è fornito perché la cifra non è ancora sufficiente, o 3
diventa pivotale e il bene è fornito ma 3 paga una tassa |v1+v2 | che è più di quanto valuta il
bene. Quindi 150 domina strettamente v3 >150.
2) -150 < v1+v2 < 0 .
• Se 3 dichiara meno di 150 e v3 <| v1+v2 | il bene non è fornito, mentre 3 preferirebbe
pagare una Clarke tax v1+v2 <150. 150 è strettamente dominante in questa occasione.
• Se dichiara qualsiasi v3 >|v1+v2 | paga sempre la stessa cifra v1+v2 quindi tale valore non
domina 150
3) v1+v2 > 0
• Il bene si fornisce comunque, 3 non è pivotale e non ha vantaggi a mentire.
17
Scelta di 1
-50
0
50
• Dichiarare la propria vera valutazione è una strategia dominante. Per ogni
dichiarazione altrui, v1 = -50 non è dominata da altre dichiarazioni e in certi casi è
strettamente dominante.
• Consideriamo tutti i possibili casi (dato che 1 non anticipa cosa dichiarano 2 e 3)
1) v3+v2< 0
• Se 1 dichiara -50 o un altro n. negativo il bene non è fornito, quindi -50 non è
dominato. 1 non ha interesse a dichiarare un n. positivo, non vuole il bene.
2) ) 0 < v3+v2 < 50 .
• Se 1 dichiara un valore negativo in val assol. minore di v3+v2 il bene è fornito,
mentre 3 preferirebbe pagare una Clarke tax pari a v3+v2 < 50. quindi -50 è
strettamente dominante in questa occasione. Dichiarare danni >50 non serve.
3) v3+v2 > 50 .
Dichiarare danni >50 o non serve oppure rende pivotali, con applicazione
di T1 che è più dannosa del bene.
18
9
Esercizio
•
•
•
•
•
1.
2.
3.
4.
5.
Un’economia è composta da due individui con le funzioni d’utilità seguenti:
U1 (x1, G) = x1G e U2 (x2, G) = x2G+G.
xi, con i=1,2 è la quantità consumata di un bene privato e G è la quantità
consumata di un bene pubblico.
Gli individui hanno le allocazioni iniziali w1= (1, 4) w2 = (1, 6)
Un’unità di bene privato può essere trasformata in un’unità di bene pubblico e
il bene privato è preso come numerario, quindi il suo prezzo è pari ad 1.
Dopo aver descritto brevemente in base a quali criteri si definisce un bene
pubblico, si tracci la frontiera di produzione nel caso sopra illustrato e la curva
d’indifferenza del primo consumatore.
Si tracci su un nuovo grafico il vincolo delle risorse del secondo agente e si
determini la quantità Pareto efficiente del bene pubblico.
Si determinino i prezzi dei due individui nell’equilibrio di Lindahl.
Si determini la quantità efficiente di bene pubblico se le allocazioni iniziali
sono w1=(1, 5) w2 = (1, 5). Commentare.
Si calcoli la quantità del bene pubblico che sarà prodotta nell’equilibrio noncooperativo.
19
10