Gli Elementi di Euclide
Libro X
Il lato e la diagonale di un quadrato sono incommensurabili
In virtù del Teorema di Pitagora il quoziente tra la diagonale ed il
lato di un quadrato è pari a 2: l’enunciato che compare nel titolo di
questo paragrafo significa che questo numero è irrazionale. Ciò è
noto dai tempi di Pitagora. Euclide, nel Libro X dei suoi Elementi,
dimostra l’asserto per via in parte aritmetica, in parte geometrica.
La Proposizione 2 afferma che
“Se di due grandezze disuguali veniamo a sottrarre, sempre e
vicendevolmente, la minore dalla maggiore [quante volte sia possibile],
e quella [ogni volta] restante non misura mai la grandezza ad essa
precedente, le grandezze saranno incommensurabili.”
Nel linguaggio degli Elementi un numero misura un altro numero se il
secondo è multiplo intero del primo. Euclide qui si riferisce ad un
procedimento che generalizza l’algoritmo delle divisioni successive
per i numeri interi. Detti a,b due numeri positivi, con a b, esistono
un quoziente intero positivo q1 ed un resto r1, tale che 0 r1< b (r1 in
generale non sarà un numero intero) in modo che si abbia:
a = q 1 b + r1 .
Se r1=0, allora a,b sono commensurabili. Altrimenti si trova
un’analoga identità che lega i numeri b, r1, con un nuovo resto r2. Se
questo è nullo, l’algoritmo si arresta, e si deduce che a,b sono
commensurabili. Altrimenti si prosegue, ripetendo il procedimento
per i numeri r1, r2, e per tutte le successive coppie di resti. Se, prima o
poi, si perviene ad un resto nullo, allora a,b sono commensurabili. In
tal caso, l’ultimo resto non nullo è la massima comune misura di a,b,
cioè il più grande numero positivo di cui a,b siano entrambi multipli
interi. Questa nozione generalizza quella di massimo comune divisore
di due numeri interi. Se l’algoritmo non produce mai un resto nullo,
allora a,b sono incommensurabili.
Se a=2 e b=1, l’algoritmo si può realizzare geometricamente nel modo
seguente.
D
C
E
G
H
F
A
B
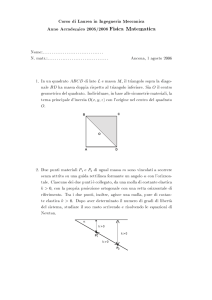
Si considera un quadrato ABCD di lato b=1. Allora a=2 è la sua
diagonale. Si riporta il lato AB sulla diagonale AC, tracciando il
punto E in modo che AE=AB. Si verifica immediatamente che la
lunghezza di EC è minore di quella di AB: dunque il primo quoziente è
1 ed il primo resto è EC. Il secondo passo dell’algoritmo richiede che
si riporti EC su BC quante più volte possibile. Si costruisca il
quadrato EFHC come in figura. Ora, essendo per costruzione EC=BF,
rimane da riportare EC su FC, tracciando il punto G. Al secondo
passo il quoziente è quindi uguale a 2 ed il resto è GC. Iterando il
procedimento si vede che ad ogni passo il resto è sempre la differenza
tra la diagonale di un quadrato ed il suo lato. Esso, pertanto, non
sarà mai uguale a zero. Con ciò è provato che 2 è irrazionale.
Una dimostrazione alternativa, esclusivamente algebrica, si ricava
sfruttando in maniera congiunta altre proposizioni di Euclide. Il
metodo è quello della reductio ad absurdum, frequentemente
impiegato dai matematici. Esso consiste nell’assumere che siano, allo
stesso tempo, vera l’ipotesi e falsa la tesi, e nel dedurne una
contraddizione.
Nel nostro caso
l’ipotesi è che a e b siano,
rispettivamente, la lunghezza della diagonale e la lunghezza del lato di
un quadrato. La tesi è che a e b sono incommensurabili. La sua
negazione è, naturalmente: a e b sono commensurabili. Supponiamo
che essa sia vera. Allora a/b è uguale al quoziente di due numeri
interi positivi, diciamo p/q. Si ha allora che
p2/q2 = a2/b2
D’altra parte, come osservato all’inizio, a/b = 2, per cui il secondo
membro è uguale a 2. Segue che
p2 = 2q2.
(*)
Ora, la Proposizione 2 del Libro IX stabilisce che, se il prodotto di
due fattori interi positivi è un numero quadrato, ed uno dei due fattori
è un numero quadrato, anche l’altro deve esserlo. Ma 2 non è un
numero quadrato. Ecco la contraddizione cercata.
Questa dimostrazione ammette una variante, che è quella
normalmente citata. Si può supporre che la frazione p/q sia ridotta ai
minimi termini. In tal caso p e q sono primi fra loro. Ora, dalla (*)
segue che p2 è pari, così che anche p è pari. Segue che p2 è divisibile
per 4. Dunque anche q è pari. Ma allora p e q non sono primi fra
loro, perché hanno in comune il fattore 2. Ciò contraddice l’ipotesi.
Questa dimostrazione era già nota ad Aristotele. Per alcuni anni 2
fu l’unico numero irrazionale noto. Altre radici quadrate irrazionali di
numeri interi furono scoperte intorno al 425 a.C. da Teodoro di
Cirene e, successivamente, da Teeteto, protagonista dell’omonimo
dialogo di Platone.