La natura della luce

La natura della luce
Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono
questi fotoni?
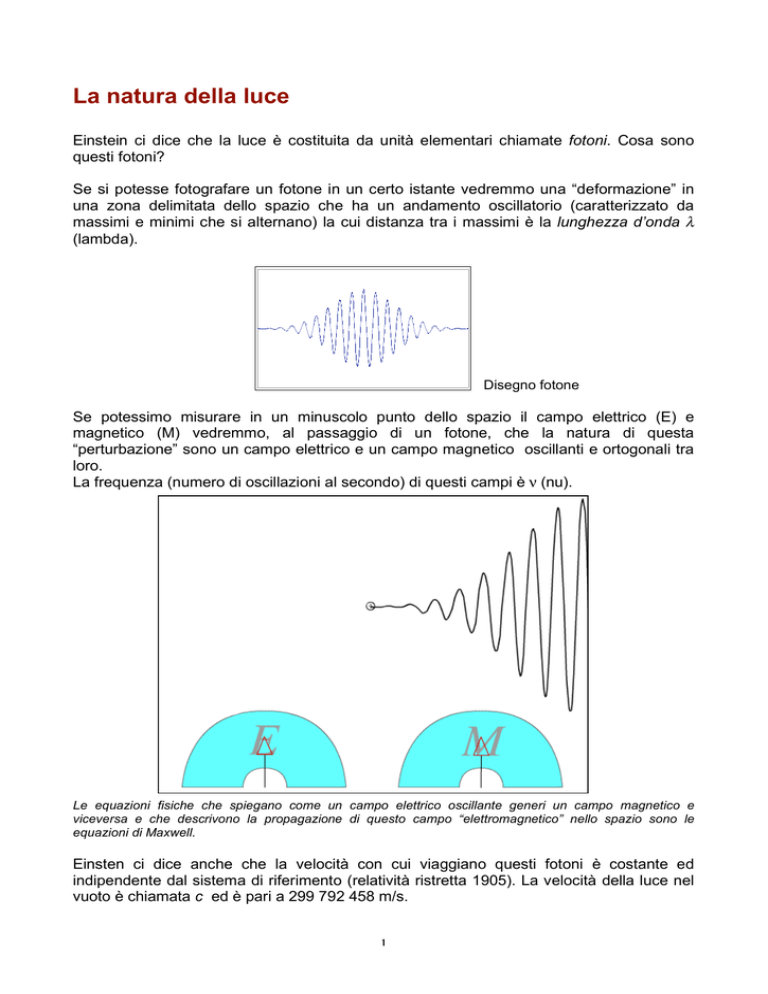
Se si potesse fotografare un fotone in un certo istante vedremmo una “deformazione” in
una zona delimitata dello spazio che ha un andamento oscillatorio (caratterizzato da
massimi e minimi che si alternano) la cui distanza tra i massimi è la lunghezza d’onda λ
(lambda).
Disegno fotone
Se potessimo misurare in un minuscolo punto dello spazio il campo elettrico (E) e
magnetico (M) vedremmo, al passaggio di un fotone, che la natura di questa
“perturbazione” sono un campo elettrico e un campo magnetico oscillanti e ortogonali tra
loro.
La frequenza (numero di oscillazioni al secondo) di questi campi è ν (nu).
Le equazioni fisiche che spiegano come un campo elettrico oscillante generi un campo magnetico e
viceversa e che descrivono la propagazione di questo campo “elettromagnetico” nello spazio sono le
equazioni di Maxwell.
Einsten ci dice anche che la velocità con cui viaggiano questi fotoni è costante ed
indipendente dal sistema di riferimento (relatività ristretta 1905). La velocità della luce nel
vuoto è chiamata c ed è pari a 299 792 458 m/s.
1
In sostanza questo fotone può essere immaginato come un’ondina lunga qualche centimetro che corre alla velocità di trecentomila chilometri al secondo nello spazio vuoto.
La lunghezza d’onda e la frequenza sono legate dalla relazione c = λ ν (la velocità della
luce è il rapporto tra la distanza tra due massimi di quest’onda (λ) e il tempo che intercorre
tra il passaggio di un massimo e il successivo (1/ν)), quindi, poiché c è una costante, un
fotone è univocamente definito da un unico parametro: ν o λ.
L’energia della luce
-34
Un singolo fotone ha un energia E = hν (costante di Plank h = 6.6256 × 10 J s). Un fascio di
luce può essere più o meno intenso, cioè trasportare più o meno energia, a seconda di
quanti fotoni è composto e della loro lunghezza d’onda.
-3
Esempio: un puntatore laser ha una potenza di circa un milliwatt, 1 mW, 10 W. Se è rosso
emette fotoni con lunghezza d’onda di circa 650 nm (nanometri, miliardesimi di metro).
8
-9
12
Quindi la sua frequenza è ν = c/λ = (3 × 10 )/(650 × 10 ) Hz = 461 × 10 Hz , cioè 461
terahertz, 461mila miliardi di oscillazioni al secondo!
-34
12
-19
L’energia del singolo fotone è E = h ν = 6.6256 × 10 × 461 × 10 = 3 × 10 J. Quindi 1 mW
15
corrisponde a circa 3,3 × 10 cioè 3,3 milioni di miliardi di fotoni al secondo! (attenzione a
non puntarlo negli occhi!!)
Una sorgente di luce ideale: il laser
Il laser può essere visto come un generatore di fotoni tutti identici fra loro (stessa
frequenza e lunghezza d’onda) tutti nelle medesima direzione e tutti in fase tra loro (cioè la
posizione dei massimi e dei minimi di un fotone coincide con quella dei fotoni vicini).
Poiché i fotoni sono moltissimi e i campi elettrici (e magnetici) dei fotoni si sommano tra
loro, in un fascio di luce laser non sono distinguibili i singoli fotoni e si può immaginare il
fascio di luce come una onda continua che viaggia in linea retta nello spazio, caratterizzata di nuovo da una frequenza e lunghezza d’onda, da una intensità (legata al
numero di fotoni) e da una dimensione trasversale.
Interferenza tra due fasci di luce
I campi elettrici (e magnetici) dei fotoni si sommano tra loro (sono dei campi vettoriali e il
campo risultante è dato dalla somma vettoriale).
2
Perciò se sovrapponiamo due fasci di luce della stessa lunghezza d’onda e della stessa
intensità, otterremo un fascio di intensità doppia.
È vero questo? Si, ma solo se le due onde sono in fase fra loro, cioè se i massimi dei due
campi elettrici sono coincidenti.
Cosa accade quando i campo elettrico di un fascio è positivo mentre l’altro è negativo?
La somma diventa una sottrazione e il campo elettrico risultante è nullo: il fascio di luce
risultante ha intensità nulla, cioè non esiste.
Questo è il principio dell’interferenza:
quando le onde sono in fase si sommano, quando sono in opposizione di fase si
annullano; in tutti i casi intermedi si avrà un’intensità intermedia tra zero e il massimo.
Nella realtà, noi non possiamo vedere le oscillazioni come sono rappresentate nella figura
perché sono troppo veloci, possiamo solo vedere (con gli occhi o con un foto-rivelatore)
l’intensità dei fasci di luce.
Quindi quello che si vedrà al variare della fase relativa tra due onde sovrapposte è un
fascio di luce di intensità variabile:
Ma, come è possibile che sovrapponendo due fasci di luce questi si annullino l’uno con
l’altro? Dove è finita l’energia?
3
La risposta sta nel metodo che si deve usare per sovrapporre due fasci di luce: uno
specchio semiriflettente (in inglese beam splitter, divisore di fascio). È uno specchio che
riflette parte della luce incidente e trasmette il rimanente.
Così come può dividere un fascio, lo specchio semiriflettente può essere usato per
combinare due fasci per osservare il fenomeno dell’interferenza.
Ma, dallo specchio semiriflettente escono anche altri due fasci di luce sovrapposti che a
loro volta possono fare interferenza costruttiva o distruttiva.
Quello che succede è che quando l’interferenza su un uscita è zero, sull’altra uscita è
massima: la somma delle due intensità è costante e l’energia si conserva.
Per semplicità, ora consideriamo lo specchio semiriflettente come un combinatore ad un
uscita sola.
Prendiamo ora un fascio di luce lo separiamo in due, poi, dopo un certo cammino, ricombiniamo i due fasci e osserviamo l’uscita.
Abbiamo costruito un INTERFEROMETRO (quello nel disegno si chiama interferometro di
Mach-Zendar).
4
La proprietà caratteristica dell’interferometro è di avere un uscita la cui intensità varia al
variare della differenza tra i cammini che compiono i due fasci di luce da quando vengono
separati a quando vengono ricombinati.
Infatti, se i due cammini fossero perfettamente identici, nel punto di ricombinazione
avrebbero la stessa fase e interferirebbero costruttivamente.
Lo stesso accadrebbe se la differenza tra i cammini fosse pari a un multiplo della
lunghezza d’onda.
Se invece la differenza di cammino fosse pari a un multiplo di mezza lunghezza d’onda, le
due onde sarebbero in opposizione di fase e l’interferenza sarebbe distruttiva.
La funzione che descrive l’intensità del segnale in funzione della differenza di cammino e
della lunghezza d’onda è: I = (I1 + I2) cos ( (L1-L2)2π/λ)
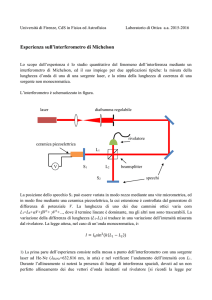
L’interferometro di Michelson
L’interferometro più utilizzato nelle misure di lunghezza è l’interferometro di Michelson.
Nell’interferometro di Michelson una sola lamina semiriflettente agisce come separatore e
ricombinatore di fascio.
La fase relativa dei due fasci di luce che arrivano all’osservatore dipende dalla differenza
di cammino che compie la luce nei due “bracci” dell’interferometro, quindi dalla posizione
dei due specchi. Immaginiamo di tenere fisso uno specchio e di muovere l’altro lungo la
direzione di provenienza della luce.
Si vede che se si muove lo specchio, la fase del fascio riflesso si muove rispetto al fascio
incidente.
5
Accadrà quindi che, all’uscita del ricombinatore, la fase relativa dei due fasci cambierà con
il movimento dello specchio, perché la lunghezza del cammino percorso da uno dei due
fasci di luce cambia rispetto all’altro.
Il risultato è che se muoviamo lo specchio il segnale in uscita varierà periodicamente da
un massimo a un minimo per ogni spostamento dello specchio di mezza lunghezza
d’onda. Infatti, se allontaniamo (o avviciniamo) lo specchio di mezza lunghezza d’onda, la
luce, che percorre il cammino una volta in avanti e una volta indietro, avrà aumentato o
diminuito il suo cammino di una lunghezza d’onda ritornando alla situazione di partenza.
Con un interferometro è possibile quindi misurare una distanza (tra due posizioni dello
specchio mobile) con una precisione almeno pari a mezza lunghezza d’onda. Ad esempio,
se utilizziamo un comune laser rosso a Elio-Neon la cui lunghezza d’onda è 633 nm, la
minima “risoluzione” dell’interferometro sarà circa 316 nm, circa un tremillesimo di
millimetro: è come potere disporre di un “metro” in cui sono incisi tre milioni di tratti.
Quando si usa un interferometro per fare una misura di lunghezza si usa come unità
di lunghezza di riferimento la lunghezza d’onda del laser.
Per questo, dal 1960 al 1983, la definizione del metro è basata sulla lunghezza
d’onda di una particolare lampada (lampada al kripto) e, ancora oggi, la realizzazione pratica del metro si basa sull’uso di interferometri equipaggiati con
particolari tipi di laser la cui lunghezza d’onda è ben definita.
Gli interferometri che si usano oggi sono un po’ più complessi di quello descritto qui, ma
funzionano sullo stesso principio. L’intensità della luce è misurata da un dispositivo
elettronico che è in grado anche di suddividere la distanza tra un massimo e il successivo
in molte parti più piccole, raggiungendo risoluzioni fino a 1 nanometro (un milionesimo di
millimetro).
Le migliori misure di lunghezza, sia nei laboratori metrologici sia nell’industria, si fanno
utilizzando gli interferometri.
6