Soluzioni

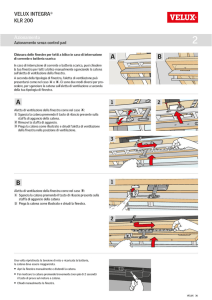
Calcolo delle Probabilità e Statistica,
Ing. Informatica e dell’Automazione, a.a. 2009/10
Prova scritta del 21/7/2010
Nota. E’ obbligatorio sia scegliere le risposte (numeriche, o le formule
…nali a seconda del caso) negli appositi spazi, sia dare la risoluzione per
esteso sul foglio a parte.
Esercizio 1. Un albergatore ha 20 camere. Quelle numerate da 1 a 10
sono camere doppie, le altre singole. Alloggia ogni cliente (o coppia) nel tipo
di camera desiderato, ma per il resto sceglie a caso il numero della camera.
i) Un giorno che ha tre doppie e due singole occupate, che probabilità c’è
che esse siano le numero 8, 9, 10, 11, 12?
1
5400
ii) In un periodo di bassa stagione le camere doppie sono poco richieste;
ogni giorno l’albergatore riceve al massimo una richiesta di camera doppia e
ciò avviene in media un giorno su due. Calcolare la probabilità che la camera
numero uno resti vuota per 10 giorni consecutivi, a partire da un certo giorno
…ssato, venendo occupata l’undicesimo giorno.
0:0299
Esercizio 2. Un sistema di trasmissione di segnali, preparato per un’emergenza,
risulta estremamente rumoroso. Esso deve solo inviare due tipi diversi di lettere, che indichiamo con 0 ed 1. Ma 0 viene ricevuto come 0 solo il 70%
delle volte (le altre è ricevuto 1), ed analogamente 1 viene ricevuto come 1
solo il 70% delle volte (le altre è ricevuto 0). In media, i messaggi inviati
contengono un ugual numero di 0 ed 1.
i) Se non si opera alcuna forma di codi…ca e si spedisce un messaggio
composto da una lettera, che probabilità c’è di riceverlo correttamente?
0:7
ii) Vista l’importanza vitale dei messaggi, si decide di limitare l’errore
spedendo per 51 volte consecutive ogni singola lettera che si vuole inviare. Il
ricevente, sa che si opera in questo modo, quindi prende gruppi di 51 simboli
ricevuti e decide che si è spedita la lettera che vede più volte, in ciascun
gruppo. Se viene “spedito 0” (con questa frase intendiamo che vengono
1
inviati 51 zeri), che probabilità c’è, ora, di sbagliare, cioè di decidere che il
mittente voleva spedire 1? Dare un valore approssimato.
2
Esercizio 3. Si consideri la funzione f (x) = C jxj e x , con
> 0
parametro reale e C constante, dipendente da , da determinare.
i) Calcolare C in modo che f sia una densità di probabilità.
C=
ii) Detta X una v.a. con densità f , calcolare la funzione di ripartizione
FX (x) di X, per x < 0, e poi trovare la funzione di ripartizione FY (y) della
v.a. Y = exp X, per y 2 (0; 1).
1
FY (y) = e
2
log2 y
iii) Calcolare E [jXj], dove X è una v.a. con densità f .
r
4
Esercizio 4. Consideriamo la catena 0
di Markov su E = f1; 2; 1
3g asociata
0
1
2
2
A, con 0
alla seguente matrice di transizione P = @ 1
2
2
1
0
1.
a) Determinare per quali valori di la catena è irriducibile e per quali
valori di è regolare.
b) Determinare, svolgendo il minimo numero di calcoli, tutte le probabilità
invarianti della catena data. Il risultato trovato dipende da ?
c) Determinare per quali valori di ci sono probabilità invarianti reversibili.
d) Dare una stima per n grande della probabilità che la catena sia nello stato
2 al tempo n + 1 e nello stato 1 al tempo n.
2
1
Soluzioni
Esercizio 1. i) La probabilità dell’evento descritto è il rapporto tra i casi
favorevoli ed i casi possibili. Il numeratore è 1. Il denominatore è il numero
di modi in cui si possono occupare tre doppie e due singole. Questo è (per
ragionamenti elementari sulle binomiali oppure ricordando l’ipergeometrica)
10
1
.
pari a 10
= 5400. Quindi la probabilità richiesta vale 5400
3
2
ii) La probabilità che in un giorno generico venga scelta la camera numero
1
. Infatti
1 è 20
P (cam1) = P (cam1junadoppia) P (unadoppia) + P (cam1jnessunadoppia) P (nessunadoppia)
1
1
1 1
+0
= :
=
10 2
2
20
Detto T il primo giorno (oggi è in giorno 1) in cui viene occupata la camera
k 1 1
(T è una v.a. geometrica), quindi
1, vale P (T = k) = 19
20
20
P (T = 11) =
19
20
10
1
= 0:0299:
20
Esercizio 2. i) La probabilità di ricevere correttamente una singola
lettera è
P (corr) = P (sped = 0; ric = 0) + P (sped = 1; ric = 1)
= P (ric = 0jsped = 0) P (sped = 0) + P (ric = 1jsped = 1) P (sped = 1)
= 0:7 0:5 + 0:7 0:5 = 0:7:
ii) Se viene “spedito 0”, il ricevente ottiene 51 simboli, ciascuno che ha
probabilità 0.7 si essere uno 0. Indichiamo con Xi , i = 1; :::; 51, la v.a. che
vale 0 se il carattere i-esimo ricevuto è 0, 1 se è 1. E’ una Bernoulli di
parametro p = 0:3. La somma S = X1 + ::: + X51 è il numero di uni ricevuti.
Il ricevente decide che il mittente ha spedito 1 (quindi sbaglia) se S > 25. In
altre parole, la probabilità di sbagliare è P (S > 25).
La v.a. S è una B (51; 0:3), quindi si potrebbe calcolare P (S > 25) usando le binomiali, ma il calcolo è troppo lungo senza un ausilio di calcolo
(non previsto per la prova d’esame, e comunque il cui merito è da attribuirsi
ai programmatori del software, non allo studente). Ad ogni modo, a titolo di
confronto numerico, usando le probabilità binomiali si ha
P (S > 25) =
51
X
k=26
51
k
0:3k 0:751
3
k
= 0:00136:
Usiamo invece l’approssimazione gaussiana, appresa nel corso, che permette di ottenere un ottimo risultato con calcoli elementari:
P (S > 25) = P (X1 + ::: + X51 > 25) = P
1
25 51 0:3
p
51 0:3 0:7
X1 + ::: + X51 51 0:3
25 51 0:3
p
>p
51 0:3 0:7
51 0:3 0:7
=1
(2:964) = 1
0:9984 = 0:0016:
Tuttavia, potevamo anche dire che
P (S > 25) = P (S
1
X1 + ::: + X51 51 0:3
26 51 0:3
p
p
51 0:3 0:7
51 0:3 0:7
26 51 0:3
p
=1
(3:269) = 1 0:9995 = 0:0005:
51 0:3 0:7
26) = P
Quindi, se vogliamo usare la correzione di continuità, scegliamo il valore
intermedio:
25:5 51 0:3
p
51 0:3 0:7
1
=1
(3:1168) = 1
0:9991 = 0:0009:
[In questo esempio la correzione di continuità non migliora il primo dei
due risultati, migliora solo il secondo; questo può accadere quando sono in
gioco probabilità molto piccole e l’approssimazione è più delicata.]
Esercizio 3. i) Vale
Z
1
1
y = x2
Z 1
Z
dy = 2xdx
x2
x2
C jxj e
dx = 2C
xe
dx
=
C
da cui C =
ii)
0
1
e
y
dy
0
(v.a. esponenziali).
Z
x
FX (x) = P (X x) =
jtj e
1
Z
1 1
1
=
e y dy =
e
2 x2
2
FY (y) = P (Y
y) = P (X
t2
dt =
y 1
x2
Z
1
= e
2
y = t2
dy = 2tdt
2
te t dt
=
x
1
x2
:
1
log y) = FX (log y) = e
2
4
log2 y
:
1
2
Z
x2
1
e
y
dy
iii)
E [jXj] =
dove
2
=
1
2
=
dove Z
N (0;
=
p
2
2
2
Z
Z
1
1
1
1
x2
2
jxj e
x2 p
1
2
2
e
dx =
x2
2 2
Z
dx =
1
x2 e
x2
2 2
dx
1
p
2
2E
Z2
)
p
2
2 2
=
p
2
1
p
2
3
r
p
= p =
:
4
2
Esercizio 4. a) Se 6= 0 e 6= 1, certamente 1 e 2 intercomunicano,
2 e 3 intercomunicano, 1 e 3 intercomunicano perché tutte le probabilità di
passaggio in un passo da uno stato all’altro sono diverse da zero. Quindi per
6= 0 e 6= 1 la catena data è irriducibile, ed è anche regolare visto che
p22 6= 0. Per 0= 1 la catena
1 è ancora irriducibile, perché dallo studio della
0 12 12
matrice P1 = @ 0 12 12 A, si vede che tutti gli stati intercomunicano (in
1 0 0
due passi al massimo)
nuovo, P22 6= 0). Per = 0 la matrice
0 ed è regolare(di
1
0 0 1
P diviene P0 = @ 1 0 0 A, quindi la catena è ancora irriducibile (tutti
0 1 0
gli stati
0 in uno o1due passi) ma non è regolare, infatti
0 comunicano
1 fra loro
1 0 0
0 1 0
P02 = @ 0 0 1 A, P03 = @ 0 1 0 A e poi si ricomincia. Ogni potenza di
0 0 1
1 0 0
P0 ha sei elementi nulli.
b) Nel presente esercizio non è necessario impostare e risolvere il sistema perché la matrice data è bistocastica per ogni
2 [0; 1], quindi la
1 1 1
distribuzione invariante risulta essere quella uniforme v =
; ;
. La
3 3 3
metodologia che si usa solitamente per determinare
la distribuzione invari8
(1
)v2 + v3 = v1
>
>
>
< v + v + (1
)v3 = v2
1
2 2
ante porterebbe alla risoluzione del sistema 2
,
>
(1
)v
1 + 2 v2 = v3
>
2
>
:
v1 + v2 + v3 = 1
5
1 1 1
; ;
. Il risultato non dipende
3 3 3
da (perché la matrice P è sempre bistocastica), ed è sempre unico (perche
la catena data è sempre irriducibile).
c) Si deve veri…care che vi pij = vj pji per ogni coppia di indici i, j, Poiché
1
1
1
vi =
per ogni i, la relazione vi pij = vj pji diviene pij = pji , da cui
3
3
3
pij = pji , cioè la matrice P deve essere simmetrica. Per ottenere questa
2
proprietà, bisogna imporre 1
= , che ha per soluzione = che è un
2
3
valore accettabile.
d) Si deve calcolare P(Xn+1 = 2; Xn = 1). Tale probabilità può essere
scritta come P(Xn+1 = 2jXn = 1) P(Xn = 1) = p12 P(Xn = 1) = 2 P(Xn = 1)
(indico con p12 l’elemento che sta nella prima riga e nella seconda colonna
della matrice P , che vale 2 ). A questo punto si sfrutta il risultato ricavato
1
al punto b), cioè P(Xn = 1)
per n “grande” (è il signi…cato della
3
distribuzione invariante che deriva dal teorema ergodico). Mettendo insieme
.
questi due risultati, si ha P(Xn+1 = 2; Xn = 1)
6
da cui di nuovo, con un po’di fatica, v =
6