STATISTICA (I modulo - Statistica Descrittiva)
Soluzione esercitazione 6
Esercizio A.
i
1
2
3
4
5
6
7
8
Totale
Alcune delle quantità utilizzate nei calcoli sono riportate nella tabella seguente:
xi
17.270
18.006
13.428
14.123
28.942
17.135
12.537
24.170
145.611
yi
2128.020
2430.049
1623.967
1799.352
3844.136
1696.326
1649.746
3112.977
18284.573
(xi − x̄)2
0.867
0.038
22.785
16.633
115.361
1.137
32.085
35.624
224.532
(yi − ȳ)2
24822.515
20873.712
437720.680
236409.524
2429122.911
347210.407
404274.225
684599.655
4585033.628
(xi − x̄)(yi − ȳ)
146.740
-28.227
3158.087
1982.986
16739.955
628.357
3601.555
4938.472
31167.925
ŷi
2156.285
2258.451
1622.965
1719.440
3776.510
2137.545
1499.283
3114.095
18284.573
(ŷi − ȳ)2
16715.125
735.527
439047.578
320504.985
2222898.253
21911.918
618250.493
686450.245
4326514.123
1. I parametri della retta di regressione y = β0 + β1 x determinati mediante il metodo dei minimi quadrati
sono:
β1
=
31167.925
= 138.81
224.532
β0
=
2285.6 − 138.81 × 18.201 = −240.88
dove N = 8, x̄ = 145.611/8 = 18.201, ȳ = 18284.573/8 = 2285.6, CXY = 31167.925, DX = 224.532.
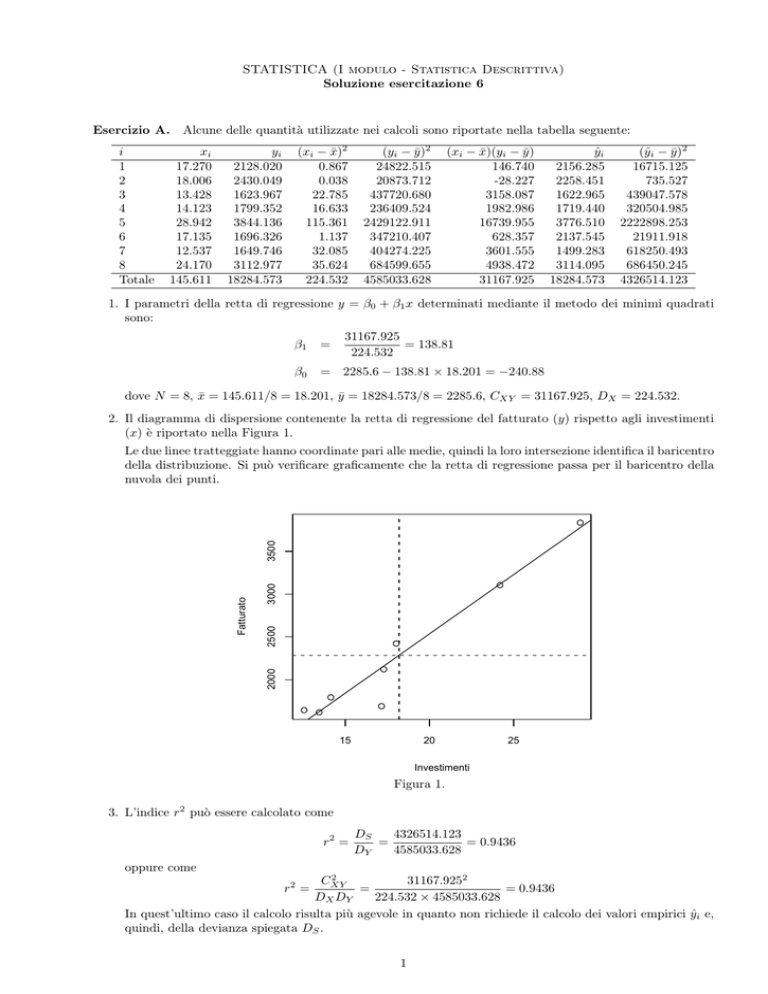
2. Il diagramma di dispersione contenente la retta di regressione del fatturato (y) rispetto agli investimenti
(x) è riportato nella Figura 1.
Le due linee tratteggiate hanno coordinate pari alle medie, quindi la loro intersezione identifica il baricentro
della distribuzione. Si può verificare graficamente che la retta di regressione passa per il baricentro della
nuvola dei punti.
2500
3000
●
●
●
2000
Fatturato
3500
●
●
●
●
●
15
20
25
Investimenti
Figura 1.
3. L’indice r2 può essere calcolato come
r2 =
DS
4326514.123
=
= 0.9436
DY
4585033.628
oppure come
2
CXY
31167.9252
=
= 0.9436
DX DY
224.532 × 4585033.628
In quest’ultimo caso il calcolo risulta più agevole in quanto non richiede il calcolo dei valori empirici ŷi e,
quindi, della devianza spiegata DS .
r2 =
1
Dal valore di r2 si deduce che la bontà di adattamento della retta di regressione ai dati è molto buona.
La percentuale della variabilità del fatturato spiegata dalla retta di regressione è pari al 94.36%.
4. L’indice di correlazione è pari a
r= √
31167.925
= 0.9714
224.532 × 4585033.628
da cui si deduce che le due variabili sono fortemente correlate in maniera positiva. Tale risultato è anche
supportato dall’inclinazione (positiva) della retta di regressione.
5. L’errore medio di predizione si può calcolare come segue:
p
√
σRL = σy 1 − r2 = 757.05 1 − 0.9436 = 179.79
p
dove σy = 4585033.628/8 = 757.05. Tale valore fornisce una misura dell’errore medio che si commette
attribuendo al fatturato i valori forniti dalla retta di regressione.
Esercizio B.
– Per la serie delle esportazioni Alcune delle quantità utilizzate sono calcolate nella tabella seguente:
Anno
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
Totale
xi (Anno−1997)
1
2
3
4
5
6
7
8
9
10
55
yi (Esportazioni)
220105
221040
260413
272990
269064
264616
284413
299923
332013
358633
2783210
(xi − x̄)2
20.25
12.25
6.25
2.25
0.25
0.25
2.25
6.25
12.25
20.25
82.50
(yi − ȳ)2
3389102656
3281112961
320696464
28419561
85692049
187827025
37112464
466646404
2882830864
6450017344
17129457792
(xi − x̄)(yi − ȳ)
261972.0
200483.5
44770.0
7996.5
4628.5
-6852.5
9138.0
54005.0
187922.0
361404.0
1125467.0
1. I parametri della retta di regressione per le esportazioni in funzione dell’anno sono i seguenti:
β1
=
1125467.0
= 13642
82.50
β0
=
278321 − 13642 × 5.5 = 203290
dove N = 10, x̄ = 55/10 = 5.5, ȳ = 2783210/10 = 278321, CXY = 1125467.0, DX = 82.50.
2. La serie storica e la retta di regressione calcolata al punto precedente sono rappresentate nel grafico a
sinistra della Figura 2.
3. Il valore previsto per le esportazioni nel 2008 è il seguente:
y2008 = 203290 + 13642 × (2008 − 1997) = 353352
con un errore medio di predizione risulta pari a:
p
√
σRL = σy 1 − r2 = 41388 1 − 0.8963 = 13328
p
dove σy = 17129457792/10 = 41388 e r2 = 1125467.02 /(82.50 × 17129457792) = 0.8963.
– Per la serie delle importazioni, alcune delle quantità utilizzate sono calcolate nella tabella seguente:
Anno
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
Totale
xi (Anno−1997)
1
2
3
4
5
6
7
8
9
10
55
yi (Importazioni)
195625
207015
258507
263757
261226
262998
285634
309292
352465
368080
2764599
2
(xi − x̄)2
20.25
12.25
6.25
2.25
0.25
0.25
2.25
6.25
12.25
20.25
82.50
(yi − ȳ)2
6534281058
4822594136
322306618
161363668
232071709
181222752
84164111
1077946790
5776775226
8394242724
27586968793
(xi − x̄)(yi − ȳ)
363757
243057
44882
19054
7617
-6731
13761
82080
266018
412290
1445786
4. I parametri della retta di regressione per le importazioni in funzione dell’anno sono i seguenti:
β1
=
1445786
= 17525
82.50
β0
=
276459.9 − 17525 × 5.5 = 180072
dove N = 10, x̄ = 55/10 = 5.5, ȳ = 2764599/10 = 276459.9, CXY = 1445786, DX = 82.50.
La serie storica delle importazioni e la retta di regressione calcolata sono rappresentate nel grafico a destra
della Figura 2.
Il valore previsto per le importazioni nel 2008 è il seguente:
y2008 = 180072 + 17525 × (2008 − 1997) = 372847
con un errore medio di predizione risulta pari a:
p
√
σRL = σy 1 − r2 = 52523 1 − 0.9184 = 15004
p
dove σy = 27586968793/10 = 52523 e r2 = 14457862 /(82.50 × 27586968793) = 0.9184.
5. Sia le esportazioni che le importazioni presentano trend crescenti, quindi i coefficienti angolari delle corrispondenti rette di regressione sono positivi. Inoltre, in entrambi i casi la bontà di adattamento della retta
ai dati risulta elevata.
350000
350000
●
●
●
●
●
200000
1
●
●
●
●
●
4
5
6
●
200000
●
●
300000
●
●
●
250000
Importazioni
300000
●
250000
Esportazioni
●
2
3
4
5
6
7
8
9
10
●
●
1
x = Anno−1997
2
3
7
8
9
10
x = Anno−1997
Figura 2.
Esercizio C.
1. Il grafico di dispersione del costo degli interventi di manutenzione rispetto all’età dell’auto è riportato in
Figura 4. Le linee tratteggiate indicano le medie delle due variabili.
3
1600
1400
●
●
1200
●
1000
●
●
●
●
●
●
●
200
400
600
800
Costo
●
●
1
2
3
4
5
Età
Figura 3.
La tabella seguente riporta le quantità necessarie per il calcolo del coefficiente di correlazione di Bravais:
1
2
3
4
5
6
7
8
9
10
11
12
Totale
xi
1
1
2
2
3
3
3
4
4
4
4
5
36
(xi − x̄)2
4
4
1
1
0
0
0
1
1
1
1
4
18
yi
253
592
741
722
851
767
1120
1055
959
1625
1600
1379
11664
(yi − ȳ)2
516961
144400
53361
62500
14641
42025
21904
6889
169
426409
394384
165649
1849292
(xi − x̄)(yi − ȳ)2
1438
760
231
250
0
0
0
83
-13
653
628
814
4844
Quindi, N = 12, x̄ = 36/12 = 3, ȳ = 11664/12 = 972, CXY = 4844, DX = 18, DY = 1849292, da cui
r= √
CXY
4844
= 0.8396
=√
DX DY
18 × 1849292
2. Il coefficiente di correlazione indica una forte relazione lineare positiva tra costi di manutenzione e età
dell’auto. Quindi, è verificata l’aspettativa per la quale ad auto più vecchie sono associati maggiori costi
di manutenzione.
4