x - Studium

Giunzione pn
Si ringrazia il Prof.
Prof Giustolisi autore dei
seguenti lucidi e figure.
Corso di Elettronica I
S. Pennisi
DIEEI - Università di CATANIA
1
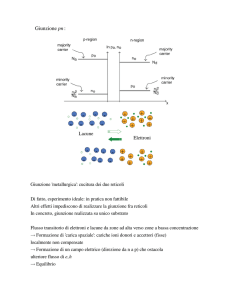
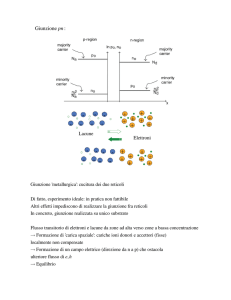
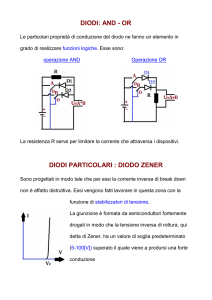
La giunzione pn
Si realizza una giunzione pn unendo due semiconduttori drogati in
maniera complementare
y
AD
A
p
n
NA
ND
x=0
K
x
z
Il suo studio è di fondamentale importanza nei dispositivi elettronici
Modello unidimensionale della
giunzione pn
Le equazioni che descrivono il comportamento del diodo sono
funzioni di x, y, z e t.
L’analisi del dispositivo si semplifica assumendo che tutte le
grandezze varino nello spazio lungo il solo asse x
A
p
n
NA
ND
x=0
K
x
Regione di carica
spaziale
Regione di carica spaziale
La realizzazione di una giunzione pn
comporta un passaggio,
passaggio per diffusione
diffusione, di
elettroni dalla regione n alla regione p (o di
lacune in dalla regione p alla regione n) che
si ricombinano
Si crea una regione di cariche fisse (ioni)
detta regione svuotata o regione di carica
spaziale
p
Il profilo di questa regione è complesso
tuttavia
u v lee due aree
ee cchee identificano
de
c o la
carica totale devono essere uguali
Per semplicità,
semplicità la regione svuotata si
assume con un profilo brusco
A
p
n
NA
ND
-xp
regione
neutra di
ti n
tipo
0
x
xn
regione di
carica spaziale
regione di
transizione
regione
g
neutra di
tipo n
0
K
regione
neutra di
ti n
tipo
regione di
x
transizione
densità di carica dovute
agli atomi ionizzati
regione di
carica spaziale
regione
g
neutra di
tipo n
-xp
0 xn
x
Elettrostatica del diodo
Le equazioni per lo studio del diodo
Adattare l’Equazione di Maxwell al caso unidimensionale per
ricavare
i
il campo elettrico nota la
l densità
d i di carica
i
div ( E ) =
ρs
εs
ρ ( x)
d
E ( x) = s
dx
εs
Utilizzare ll’Equazione
Equazione di Poisson per ricavare il potenziale
elettrico nota la densità di carica
ρs ( x )
d2
d
V ( x) = −
E ( x) = − V ( x)
2
dx
εs
dx
Scrivere la densità di carica in un semiconduttore
ρ s ( x) = q ⎡⎣ p ( x) − n( x) + N D+ ( x) − N A− ( x) ⎤⎦
La giunzione brusca o a gradino
Lo studio del diodo è abbastanza complesso. Si farà uso delle
seguenti ipotesi semplificative
1. la concentrazione di drogante varia
b
bruscamente
t passando,
d nell punto x = 0,
0 dda NA
a ND e mantenendosi costante all’interno del
semiconduttore
NA
x≤0
ND
x≥0
2. la regione di carica spaziale è
completamente svuotata di portatori liberi e
t tti gli
tutti
li atomi
t i di drogante
d
t sono ionizzati
i i ti
(ipotesi di approssimazione di svuotamento)
n=0
N D+ = N D
p=0
N A− = N A
3 all’esterno
3.
all esterno della regione di carica spaziale,
la concentrazione di portatori liberi diventa
bruscamente uguale alla concentrazione di
drogante (approssimazione di quasi neutralità)
n = ND
p = NA
ρs = 0
Il campo elettrico
Il campo elettrico si ricava partendo
dalla seguente equazione
Vbi
ρ s ( x)
E ( x) = ∫ dE = ∫
dx
εs
A
p
n
NA
ND
K
dove
⎧−qN A
⎪⎪
ρ s ( x) = ⎨qqN D
⎪0
⎪⎩
x ∈ ⎡⎣ − x p ,0 ⎤⎦
x ∈ [ 0,, xn ]
densità di
carica
qND
-xp
altrove
0
-qNA
Per la conservazione della carica si ha
N D xn = N A x p
xn
x
Il campo elettrico
La soluzione generale dell’equazione è
⎧ qN A
⎪− ε x + C1
⎪
s
E ( x) = ⎨
⎪ qN D x + C
2
⎪⎩ ε s
x ∈ ⎡⎣ − x p ,0 ⎤⎦
x ∈[ 0, xn ]
Le condizioni al contorno implicano che il campo deve essere
nullo per x = xn e x = –xxp,ossia
−
qN A
εs
qN D
εs
(−x ) + C
p
xn + C2 = 0
1
=0
C1 = −
qN A x p
C2 = −
qN D
εs
εs
xn
Il campo elettrico
⎧ qN
NA
x + x p ) x ∈ ⎡⎣ − x p ,0 ⎤⎦
(
⎪−
⎪ εs
⎪⎪ qN D
E ( x) = ⎨
( x − xn ) x ∈ [0, xn ]
⎪ εs
⎪
⎪0
altrove
⎪⎩
Vbi
A
campo
elettrico
p
n
NA
ND
-xp
0
K
xn
x
Il campo elettrico risulta nullo al di
fuori della regione svuotata e ha un
andamento
d
li
lineare all’interno
ll’i
Ha un valore massimo per x = 0
EM = E (0) =
qN A
εs
xp =
qN D
εs
xn
Il potenziale elettrico
Il potenziale elettrico si ottiene
risolvendo
i l d la
l seguente equazione
i
V ( x ) = − ∫ E ( x)dx
Vbi
A
p
n
NA
ND
K
dove il campo elettrico è
⎧ qN A
x + x p ) x ∈ ⎡⎣ − x p ,0 ⎤⎦
(
⎪−
⎪ εs
⎪⎪ qN D
E ( x) = ⎨
( x − xn ) x ∈ [0, xn ]
⎪ εs
⎪
⎪0
altrove
⎪⎩
campo
elettrico
-xp
0
xn
x
Il potenziale elettrico
La soluzione generale dell’equazione è
⎧C3
⎪
2
⎪ qN A
x
x
+
p ) + C4
⎪⎪ 2ε (
V ( x) = ⎨ s
⎪− qN D ( x − x )2 + C
n
5
⎪ 2ε s
⎪
⎪⎩C6
x ∈ ⎦⎤ −∞, − x p ⎦⎤
x ∈ ⎡⎣ − x p ,0 ⎤⎦
x ∈ [ 0, xn ]
x ∈ [ xn , +∞[
Rimangono da ricavare le condizioni al contorno
Il potenziale elettrico
• La prima condizione al contorno comporta la scelta di un
potenziale di riferimento (potenziale
(
i l nullo)
ll )
• Scegliamo come potenziale nullo il potenziale nella regione p
V ( x) = 0 x ≤ −xp
C3 = 0
• La seconda condizione al contorno comporta l’assegnazione di
un potenziale nella regione di tipo n
• Anch’esso è un valore costante e la sua espressione verrà
ricavata fra breve
• Assumiamo il suo valore noto e pari a Vbi
V ( x ) = Vbi x ≥ xn
C6 = Vbi
Il potenziale elettrico
Le altre due condizioni al contorno vengono imposte tenendo
conto che
h V(x)
( ) ddeve essere continua per x = xn e x =–xp
2
qN A
⎡ ( − x p ) + x p ⎤ + C4 = 0
⎦
2ε s ⎣
2
q D
qN
−
⎡( xn ) − xn ⎤⎦ + C5 = Vbi
⎣
2ε s
C4 = 0
C5 = Vbi
Resta da ricavare la quantità Vbi. Per essa basta applicare
p1
V21 = VT ln
p2
dove p1 = NA e p2 = ni2/ND
⎛ N A N D ⎞ Potenziale di giunzione
Vbi = VT ln ⎜
⎟
2
n
⎝ i ⎠ o di contatto
Il potenziale elettrico
Vbi
⎧0
⎪
2
⎪ qN A
x
x
+
p)
⎪⎪ 2ε (
V ( x) = ⎨ s
⎪− qN D ( x − x )2 + V
n
bi
⎪ 2ε s
⎪
⎪⎩Vbi
x ∈ ⎤⎦ −∞, − x p ⎤⎦
x ∈ ⎡⎣ − x p ,0 ⎤⎦
x ∈ [ 0, xn ]
x ∈ [ xn , +∞[
A
p
n
NA
ND
K
potenziale
-xp
xn
Vbi
0
Il potenziale elettrico è costante all’esterno della regione svuotata ed
ha un andamento q
quadratico al suo interno
x
Larghezza della regione svuotata
La larghezza della regione
svuotata, W, è pari a
E(x)
-xxp
W
0
xn
x
EM
W = xn + x p
Vbi
e tenendo conto che
Dalla figura si ha
1
Vbi = EM W
2
N D xn = N A x p
sii ha
h
d cuii
da
NA
xn =
W
ND + N A
2ε s N D + N A
W=
Vbi
q ND N A
EM =
2ε s
Vbi = xnW
qN D
qN D
εs
xn
Larghezza della regione svuotata
La regione svuotata dipende dalla concentrazione di drogante
La relazione ricavata può essere semplificata nel caso di un lato
con una concentrazione molto maggiore dell
dell’altro
altro (caso frequente)
⎧ 2ε s
Vbi per N D >> N A
⎪
⎪ qN A
W =⎨
⎪ 2ε s
⎪ qN Vbi per N A >> N D
D
⎩
La regione svuotata si estende principalmente nel lato a minore
concentrazione di drogante
g
Riepilogo dell
dell’analisi
analisi del diodo a
giunzione brusca
A
Densità di
carica
⎧ −qN A
⎪⎪
ρ s ( x) = ⎨ qN D
⎪0
⎪⎩
x ∈ ⎡⎣ − x p ,0 ⎤⎦
Vbi
p
n
NA
ND
K
x ∈ [ 0, xn ]
altrove
l
densità di
carica
qND
-xp
Bilancio di
carica
N D xn = N A x p
C po
Campo
elettrico
⎧ qN A
( x + x p ) x ∈ ⎡⎣− x p ,0⎤⎦
⎪−
ε
s
⎪
⎪⎪ q
qN
E ( x) = ⎨ D ( x − xn )
x ∈ [ 0,
0 xn ]
ε
⎪ s
⎪
⎪0
altrove
⎪⎩
0
x
xn
-qNA
campo
elettrico
-xp
xn
0
x
potenziale
-xp
xn
0
Vbi
x
Riepilogo dell
dell’analisi
analisi del diodo a
giunzione brusca
Potenziale
elettrico
⎧0
⎪
2
⎪ qN A
x
x
+
(
)
p
⎪⎪ 2ε s
V ( x) = ⎨
⎪− qN D ( x − x )2 + V
n
bi
⎪ 2ε s
⎪
⎪⎩Vbi
x ∈ ⎤⎦ −∞, − x p ⎤⎦
A
Vbi
p
n
NA
ND
K
x ∈ ⎡⎣ − x p ,0 ⎤⎦
x ∈ [ 0, xn ]
densità di
carica
qND
-xp
x ∈ [ xn , +∞[
0
xn
x
-qNA
Potenziale
di contatto
⎛N N ⎞
Vbi = VT ln ⎜ A 2 D ⎟
⎝ ni ⎠
Regione
svuotata
⎧ 2ε s
Vbi per N D >> N A
⎪
qN
A
⎪
W =⎨
⎪ 2ε s
⎪ qN Vbi per N A >> N D
D
⎩
campo
elettrico
-xp
xn
0
x
potenziale
-xp
xn
0
Vbi
x
Giunzione lineare
È un modello alternativo alla giunzione brusca nel quale la densità
di carica
i varia
i linearmente
li
con la
l distanza
di
ρ s ( x) = qax
In questo caso la legge della conservazione della carica porta a
x p = xn = W 2
Il campo elettrico si ricava integrando
ρ ( x)
qa
E ( x) = ∫ dE = ∫ s
dx =
xdx
∫
εs
εs
La cui soluzione generale è
E ( x) =
qa 2
x + C7
2ε s
Giunzione lineare
La condizione al contorno implica la continuità per x = ±W/2 dove
il campo deve
d
avere valore
l
nullo
ll
2
qa ⎛ W ⎞
⎜ ± ⎟ + C7 = 0
2ε s ⎝ 2 ⎠
qa ⎛ W ⎞
C7 = −
⎜ ⎟
2ε s ⎝ 2 ⎠
2
da cui
qa ⎛ 1 2
2⎞
E ( x) = −
W
x
−
⎜
⎟
2ε s ⎝ 4
⎠
Il potenziale elettrico si ottiene integrando l’opposto del campo
elettrico
l i
V ( x ) = − ∫ E ( x)dx = ∫
qa ⎛ 1 2
2⎞
W
x
−
⎜
⎟ dx
2ε s ⎝ 4
⎠
Giunzione lineare
La soluzione generale è
qa ⎛ 1 2
1 3⎞
V ( x) =
⎜ W x − x ⎟ + C8
2ε s ⎝ 4
3 ⎠
• La condizione al contorno comporta la scelta di un potenziale di
riferimento (potenziale nullo)
• Imponendo nullo il potenziale per x = –W/2
qa
2ε s
⎡1 2 ⎛ W
⎢ W ⎜−
⎝ 2
⎢⎣ 4
3
⎞ 1⎛ W ⎞ ⎤
⎟ − ⎜ − ⎟ ⎥ + C8 = 0
⎠ 3 ⎝ 2 ⎠ ⎥⎦
qa 1 3
C8 =
W
2ε s 12
d cuii
da
qa ⎛ 1 3 1 2
x ⎞⎛ 1 x ⎞
1 3 ⎞ qaW 3 ⎛
V ( x) =
W
+
W
x
−
x
=
1
−
⎜
⎟
⎜
⎟⎜ + ⎟
2ε s ⎝ 12
4
3 ⎠
6ε s ⎝ W ⎠⎝ 2 W ⎠
2
Giunzione lineare
Poiché
⎛W
Vbi = V ⎜
⎝ 2
q 3
⎞ qaW
⎟=
⎠ 12ε s
invertendo si trova la larghezza della regione svuotata,
svuotata W
W=
3
12ε s
Vbi
qa
tenendo conto della quale si ha per V(x)
x ⎞⎛ 1 x ⎞
⎛
V ( x) = 2Vbi ⎜1 − ⎟⎜ + ⎟
⎝ W ⎠⎝ 2 W ⎠
Ovviamente anche in questo caso si ha
2
⎛N N ⎞
Vbi = VT ln ⎜ A 2 D ⎟
⎝ ni ⎠
Riepilogo dell
dell’analisi
analisi del diodo a
giunzione lineare
A
Densità di carica
ρ s ( x) = qax
Bilancio di carica
x p = xn = W 2
C
Campo
elettrico
l i
qa ⎛ 1 2
2⎞
E ( x) = −
W
−
x
⎜
⎟
2ε s ⎝ 4
⎠
Potenziale di contatto
⎛N N ⎞
Vbi = VT ln ⎜ A 2 D ⎟
⎝ ni ⎠
Potenziale elettrico
x ⎞⎛ 1 x ⎞
⎛
V ( x) = 2Vbi ⎜1 − ⎟⎜ + ⎟
⎝ W ⎠⎝ 2 W ⎠
Regione svuotata
12ε s
W=3
Vbi
qa
Vbi
p
n
NA
ND
K
densità di
carica
-W/2
0
campo
elettrico
-W/2
x
W/2
W/2
0
x
2
potenziale
-W/2
W/2
0
Vbi
x
Giunzione pn fuori
dall’equilibrio
Le ipotesi di studio
L’applicazione di una tensione, VD, ai capi del diodo porta la
giunzione
i i
f i dalla
fuori
d ll condizione
di i
di equilibrio
ilib i
Il diodo può comunque essere analizzato e descritto ricorrendo alle
equazioni già determinate in zona di equilibrio,
equilibrio assumendo che
Vbi - VD
1. valga l’ipotesi di approssimazione
di svuotamento (tutti gli atomi di
n
drogante dentro la regione di carica A p
NA
ND
spaziale siano ionizzati)
2. trascurando le cadute di tensione
VD
all’esterno della regione svuotata.
La condizione 2 implica che tutta la tensione VD sarà applicata tra
–xxp e xn. Quindi,
Quindi VD si andrà a sovrapporre al potenziale interno Vbi
K
La regione svuotata
Le soluzioni saranno quelle già trovate sotto la condizione di
equilibrio nelle quali,
quali al potenziale interno in equilibrio Vbi si
sostituirà la differenza tra il potenziale interno in equilibrio e la
tensione applicata ossia Vbi – VD
Ad esempio, la larghezza della regione svuotata W risulterà
⎧ 2ε s
(Vbi − VD )
⎪
⎪ qN A
W =⎨
⎪ 2ε s
⎪ qN (Vbi − VD )
D
⎩
per
N D >> N A
per
N A >> N D
Essa diminuisce per VD > 0 e aumenta per VD < 0
Polarizzazione diretta
1. Se VD > 0 il diodo si trova in
polarizzazione diretta
2. Il potenziale applicato (VD) si
oppone al potenziale interno
all’equilibrio (Vbi) e il risultato
complessivo sarà la riduzione
della differenza di potenziale ai
capi della regione svuotata
Vbi - VD
VD
A
p
NA
cariche fisse
lac ne
lacune
W0
W
n, p
pp00
nn
pp
np
3. Indicheremo
d c e e o i nuovi
uov es
estremi
e
della regione svuotata con –xp e
xn, mentre i vecchi valori
verranno indicati con –xp0 e xn0
elettroni
liberi
n
ND
nn0
pn
Δn
Δp
np0
pn0
0
-xp0
-xp
xn
xn0
x
K
Barriera in polarizzazione diretta
1. Si crea un abbassamento della
barriera di potenziale che
limitava la diffusione di
portatori dalle regioni a maggior
concentrazione a quelle a minor
concentrazione
2. Gli elettroni diffondono da
destra a sinistra
3. Le lacune diffondono da sinistra
a des
destra
4. Il fenomeno può essere visto
come un’iniezione
un iniezione di portatori
Vbi - VD
VD
A
p
NA
cariche fisse
elettroni
liberi
n
ND
lac ne
lacune
W0
W
n, p
pp00
nn
pp
np
nn0
pn
Δn
Δp
np0
pn0
0
-xp0
-xp
xn
xn0
x
K
Elettroni in polarizzazione diretta
1. Δn elettroni transitano attraverso
la regione svuotata e si riversano
nella regione p
2. In –xxp, la concentrazione di
elettroni aumenta di Δn
Vbi - VD
VD
A
p
NA
cariche fisse
lac ne
lacune
n p ( − x p ) = n p 0 + Δn
3. Per la conservazione della carica
le lacune aumentano di Δn
p p ( − x p ) = p p 0 + Δn
4 Assumendo bassi livelli di
4.
iniezione
p p ( − xp ) ≈ pp0
n p ( − x p ) ≈ Δn
elettroni
liberi
n
ND
W0
W
n, p
pp00
nn
pp
np
nn0
pn
Δn
Δp
np0
pn0
0
-xp0
-xp
xn
xn0
x
K
Lacune in polarizzazione diretta
1. Δp lacune transitano attraverso la
regione svuotata e si riversano
nella regione n
2. In xn, la concentrazione di
VD
lacune aumenta di Δp
Vbi - VD
A
p
NA
cariche fisse
lac ne
lacune
pn ( xn ) = pn 0 + Δp
3. Per la conservazione della carica
gli elettroni aumentano di Δpp
g
nn ( xn ) = nn 0 + Δp
4 Assumendo bassi livelli di
4.
iniezione
nn ( xn ) ≈ nn 0
pn ( xn ) ≈ Δp
elettroni
liberi
n
ND
W0
W
n, p
pp00
nn
pp
np
nn0
pn
Δn
Δp
np0
pn0
0
-xp0
-xp
xn
xn0
x
K
Polarizzazione inversa
1. Se VD = –VR < 0 il diodo si
trova in polarizzazione inversa
2. Il potenziale applicato (VR) si
somma al potenziale interno
all’equilibrio (Vbi) e il risultato
complessivo sarà l’aumento
della differenza di potenziale ai
capi della regione svuotata
3. Indicheremo
d c e e o i nuovi
uov es
estremi
e
della regione svuotata con –xp e
xn, mentre i vecchi valori
verranno indicati con –xp0 e xn0
Vbi +VR
A
p
NA
elettroni
liberi
cariche fisse
K
lacune
n
ND
VR
W0
W
n, p
nn
pp
pp00
np0
np
Δn
-xp -xp0
Δp
0 xn0 xn
nn0
pn00
pn
x
Barriera in polarizzazione inversa
1. Si crea un innalzamento della
barriera di potenziale che interdice
ancor di più la diffusione di
portatori
2. Il campo elettrico attira le
cariche ai bordi della regione
svuotata
3. Gli elettroni si muoveranno da
sinistra a destra e le lacune da
destra a sinistra (corrente di
deriva)
de
v )
4. Il numero di cariche che
transitano è però limitato dalle
basse concentrazioni in gioco
Vbi +VR
A
p
NA
elettroni
liberi
cariche fisse
K
lacune
n
ND
VR
W0
W
n, p
nn
pp
pp00
np0
np
Δn
-xp -xp0
Δp
0 xn0 xn
nn0
pn00
pn
x
Elettroni in polarizzazione inversa
1. Δn elettroni transitano verso la
regione n
2. In –xp, la concentrazione di
elettroni diminuisce di Δn
Vbi +VR
A
n p ( − x p ) = n p 0 − Δn
3 P
3.
Poiché
i hé Δn
Δ puòò essere all più
iù parii a
np0, oltre un certo valore di VR, si ha
np ( − xp ) ≈ 0
4. La corrente satura e raggiunge un
valore
l
massimo
i
indipendente
i di d t da
d VR
5. I portatori maggioritari rimangono
inalterati
p
NA
elettroni
liberi
cariche fisse
K
lacune
n
ND
VR
W0
W
n, p
nn
pp
pp00
np0
np
Δn
-xp -xp0
Δp
0 xn0 xn
nn0
pn00
pn
x
Lacune in polarizzazione inversa
1. Δp lacune transitano verso la
regione p
2. In xn, la concentrazione di lacune
diminuisce di Δp
Vbi +VR
A
p
NA
elettroni
liberi
cariche fisse
n
ND
pn ( xn ) = pn 0 − Δp
3 P
3.
Poiché
i hé Δp
Δ puòò essere all più
iù parii a
pn0, oltre un certo valore di VR, si ha
pn ( xn ) ≈ 0
4. La corrente satura e raggiunge un
valore
l
massimo
i
indipendente
i di d t da
d VR
5. I portatori maggioritari rimangono
inalterati
K
lacune
VR
W0
W
n, p
nn
pp
pp00
np0
np
Δn
-xp -xp0
Δp
0 xn0 xn
nn0
pn00
pn
x
Riepilogo dell
dell’analisi
analisi qualitativa
L’applicazione di un potenziale esterno ai capi di un diodo causa
1 Una variazione della larghezza della regione svuotata
1.
2. Una variazione della concentrazione dei portatori
minoritari agli estremi della regione svuotata
Polarizzazione diretta
Polarizzazione inversa
1. La larghezza W diminuisce
2 La
2.
L concentrazione
t i
dei
d i
portatori maggioritari
rimane immutata
3. La concentrazione dei
portatori minoritari
aumenta
1. La larghezza W aumenta
2 La
2.
L concentrazione
t i
dei
d i
portatori maggioritari
rimane immutata
3. La concentrazione dei
portatori minoritari tende
a zero
Portatori al contorno della regione
svuotata
Le equazioni di Boltzmann permettono di ottenere le concentrazioni
noto il potenziale tra due regioni
n1 = n2 e−V21 VT
p1 = p2 eV21 VT
Se la regione 1 si trova nel punto –xxp (regione p) e la regione 2 nel
punto xn (regione n), per VD = 0 si ha
pn 0 = p p 0 e −Vbi
VT
= N A e −Vbi
VT
n p 0 = nn 0 e −Vbi
VT
= N D e −Vbi
VT
quindi applicando VD e sostituendo a Vbi il potenziale Vbi – VD
quindi,
pn ( xn ) = p p ( − x p ) e
− (Vbi −VD ) VT
n p ( − x p ) = nn ( xn ) e
− (Vbi −VD ) VT
Portatori al contorno della regione
svuotata
)
)
p ( x ) = p (−x ) e (
n (−x ) = n ( x ) e (
− Vbi −VD VT
n
n
p
p
− Vbi −VD VT
p
p
n
n
Nel caso di bassi livelli di iniezione pp e nn non variano e si ha
(
)
pn ( xn ) = N A e−Vbi VT eVD VT
(
)
n p ( − x p ) = N D e−Vbi VT eVD VT
e poiché come visto prima è
pn 0 = N A e −Vbi
VT
n p 0 = N D e −Vbi
VT
Si ottengono le seguenti concentrazioni di portatori minoritari in
funzione di VD ai capi della regione svuotata
pn ( xn ) = pn 0 eVD VT
n p ( − x p ) = n p 0 eVD VT
Portatori al contorno della regione
svuotata
In presenza di un potenziale esterno, la concentrazione di portatori
minoritari agli estremi della regione svuotata aumenta se VD > 0 e
di i i
diminuisce
t d d a zero per VD < 0
tendendo
La variazione di portatori minoritari rispetto alla condizione di
equilibrio (indicata prima con Δn e Δp), può essere vista come una
iniezione di portatori ai bordi della regione di carica
pn′ ( xn ) = pn 0
(
2
n
eVD VT − 1 = i eVD VT − 1
ND
(
)
n′p ( − x p ) = n p 0 e
VD VT
(
)
ni2 VD VT
−1 =
e
−1
NA
)
(
)
Profili dei portatori
p
minoritari e caratteristica
tensione- corrente del
diodo
Analisi qualitativa del profilo dei
portatori minoritari
Se applichiamo ad un diodo una tensione positiva VD le
concentrazioni dei portatori minoritari ai capi della regione
svuotata
t t aumenteranno
t
secondo
d
ni2 VD VT
e
−1
pn′ ( xn ) =
ND
(
)
ni2 VD VT
e
n′p ( − x p ) =
−1
NA
(
)
Tale aumento può essere visto come una iniezione di portatori
Sappiamo già che i portatori diffonderanno all’interno del
semiconduttore e si ricombineranno con i portatori maggioritari
La loro concentrazione diminuirà esponenzialmente man mano
che ci si allontanerà dal punto di iniezione
Studio analitico dei profili di portatori
Le equazioni differenziali che governano il profili di
concentrazione per le lacune e per gli elettroni sono date da
pn′ ( x )
∂2
pn′ ( x ) = 2
2
∂x
Lp
n′p ( x )
∂2
n′p ( x ) =
2
∂x
L2n
dove Lp e Ln sono le lunghezze di diffusione rispettivamente delle
lacune e degli elettroni
La loro risoluzione va ricercata ricavando la solita soluzione
generale e applicando le opportune condizioni al contorno
Lo studio
L
t di viene
i
classicamente
l i
t distinto
di ti t in
i due
d casi:
i
1) il diodo è a base lunga
2) il diodo è a base corta
Diodo a base lunga: definizione
Un diodo viene detto a base lunga se se le lunghezze delle regioni
neutre sono molto maggiori delle lunghezze di diffusione delle
lacune e degli elettroni, cioè se
ln′ >> L p
l ′p >> Ln
A
p
NA
VD
Idealmente, un diodo a base lunga
può essere visto come una
giunzione pn le cui regioni neutre si
estendono indefinitamente lungo
g
l’ascissa
K
n
ND
W
n, p
pp = ppp0 = NA
np(-xp)
n’p
nn = nn0 = ND
pn(xn)
( )
np(x)
pn(x)
np0
-llp
p’n
pn0
-xxp 0 xn
l’p
pp
ln
l’n
x
Diodo a base lunga: profilo dei
portatori
Consideriamo le lacune
La soluzione
L
l i
generale
l
dell’equazione di continuità è
pn′ ( x ) = K1e
− x Lp
+ K 2e
A
p
NA
VD
x Lp
W
n, p
pp = ppp0 = NA
e le condizioni al contorno sono
date da
2
i
(
n
eVD
ND
pn′ ( x → ∞ ) = 0
pn′ ( x = xn ) =
K
n
ND
VT
)
−1
np(-xp)
n’p
nn = nn0 = ND
pn(xn)
( )
np(x)
pn(x)
np0
-llp
p’n
pn0
-xxp 0 xn
l’p
pp
ln
l’n
x
Diodo a base lunga: profilo dei
portatori
Il profilo delle lacune iniettate è
ppertanto dato da
A
pn′ ( x ) =
2
i
(
n
eVD
ND
VT
)
−1 e
− ( x − xn ) L p
p
NA
VD
K
n
ND
W
Analogamente per gli elettroni
iniettati si trova
n, p
pp = ppp0 = NA
np(-xp)
2
i
(
)
n
( x+ x )
n′p ( x) =
eVD VT − 1 e p
NA
Ln
n’p
nn = nn0 = ND
pn(xn)
( )
np(x)
pn(x)
np0
-llp
p’n
pn0
-xxp 0 xn
l’p
pp
ln
l’n
x
Diodo a base lunga: correnti di
diffusione dei portatori minoritari
Dai profili dei portatori iniettati si può risalire alle correnti di
diffusione
qD p ni2 VD VT
d
− ( x − xn ) L p
e
j p ( x) = − qD p
pn′ ( x) =
−1 e
N D Lp
dx
(
)
qDn ni2 VD VT
d
( x+ x )
e
jn ( x) = qDn n′p ( x) =
−1 e p
N A Ln
dx
(
)
Ln
Tali correnti decrescono allontanandosi dalla regione svuotata
Questo vuol dire che i portatori minoritari si stanno ricombinando
con i portatori maggioritari
Esiste allora una corrente di portatori maggioritari proveniente
dai terminali K e A che compensa la diminuzione di jp(x) e jn (x)
Diodo a base lunga: correnti dovute
alla diffusione delle lacune
• per x > xn jp decresce ma è rimpiazzata da una corrente di
elettroni entranti dal catodo (K)
• per x < xn
jp è pari a jp(xn)
VD
La corrente dovuta alla diffusione
di lacune è costante lungo tutto il
semiconduttore ed è ppari a
j p = j p ( xn ) =
qD p ni2
N D Lp
(
VD VT
e
)
−1
A
p
NA
corrente di cariche
positive entranti
dall’anodo
j
jn
K
n
ND
W
corrente di cariche
negative entranti dal
catodo
jn(x)
jp(x)
-lp
-xp
0
xn
lp’
jp è data
d da
d jp(x)
( ) valutata nel punto dii iniezione,
i i i
xn
jp
ln
ln’
x
Diodo a base lunga: correnti dovute
alla diffusione degli elettroni
• per x < –xp jn decresce ma è rimpiazzata da una corrente di
lacune entranti dall’anodo
• per x > –xp jn è pari a jn(–xp )
La corrente dovuta alla diffusione
di elettroni è costante lungo tutto il
semiconduttore ed è ppari a
qDn ni2 VD VT
e
−1
jn = jn ( − x p ) =
N A Ln
(
)
VD
A
p
NA
corrente di cariche
positive entranti
dall’anodo
j
jn
K
n
ND
W
corrente di cariche
negative entranti dal
catodo
jn(x)
jp(x)
-lp
-xp
lp’
0
xn
jp
ln
ln’
jn è data
d da
d jn(x)
( ) valutata nel punto dii iniezione,
i i i
–xp
x
Diodo a base lunga: corrente totale
La densità di corrente totale del diodo è data dalla somma di jp e jn
jD = jn + j p =
⎛ Dn
D p ⎞ VD VT
= qn ⎜
+
e
−1
⎜ N A Ln N D Lp ⎟⎟
⎝
⎠
(
2
i
)
Nel caso in cui una regione sia
molto più drogata dell
dell’altra
altra si ha
⎧ 2
⎪qni
⎪
jD = ⎨
⎪qn 2
⎪⎩ i
(
)
Dn
eVD VT − 1
N A Ln
Dp
N D Lp
(e
VD VT
)
−1
se N D >> N A
VD
A
p
NA
corrente di cariche
positive entranti
dall’anodo
j
jn
W
corrente di cariche
negative entranti dal
catodo
jn(x)
jp(x)
-lp
se N A >> N D
K
n
ND
-xp
lp’
0
xn
jp
ln
ln’
x
Diodo a base corta: definizione
Un diodo viene detto a base corta se se le lunghezze delle regioni
neutre sono molto minori delle lunghezze di diffusione delle
lacune e degli elettroni, cioè se
ln′ < L p
l ′p < Ln
In un diodo a base corta i portatori
minoritari prima di arrivare ai
terminali elettrici devono
attraversare uno spazio più
ristretto rispetto al diodo a base
lunga
u g
A
p
NA
VD
W
n, p
nn = nn0 = ND
pp = ppp0 = NA
np(-xp)
pn(xn)
np(x)
np’
np0
I portatori minoritari non hanno il
tempo necessario per ricombinarsi
K
n
ND
-lp
p’n
pn0
-xp
l’p
pp
pn(x)
0
xn
ln
l’n
x
Diodo a base corta: profilo dei
portatori
Consideriamo le lacune
Poiché
P
i hé non avviene
i
alcuna
l
ricombinazione, è come se il tempo
di vita medio τp (e quindi Lp) fosse
infinito
A
p
NA
VD
K
n
ND
W
n, p
nn = nn0 = ND
pp = ppp0 = NA
L’equazione di continuità diventa
np(-xp)
∂ pn′ ( x )
2
∂x 2
=
pn′ ( x )
∂ pn′ ( x )
L2p
∂x 2
2
=0
pn(xn)
np(x)
np’
np0
-lp
p’n
pn0
-xp
l’p
pp
pn(x)
0
xn
ln
l’n
x
Diodo a base corta: profilo dei
portatori
La soluzione generale è
pn′ ( x ) = K1 x + K 2
A
VD
Mentre le condizioni al contorno
impongono che
ni2 VD
pn′ ( x = xn ) =
e
ND
pn′ ( x = ln ) = 0
(
VT
)
−1
p
NA
W
n, p
nn = nn0 = ND
pp = ppp0 = NA
np(-xp)
pn(xn)
np(x)
np’
La ricombinazione avviene
istantaneamente al ppunto x = ln
K
n
ND
np0
-lp
p’n
pn0
-xp
l’p
pp
pn(x)
0
xn
ln
l’n
x
Diodo a base corta: profilo dei
portatori
Il profilo delle lacune iniettate è
ppertanto dato da
pn′ ( x ) =
2
i
(
n
eVD
ND
VT
A
⎛
x − xn ⎞
− 1 ⎜1 −
⎟
′
l
n
⎝
⎠
)
p
NA
VD
K
n
ND
W
Analogamente per gli elettroni
iniettati si trova
⎛ x + xp ⎞
ni2 VD VT
n′p ( x) =
e
− 1 ⎜1 +
⎟⎟
⎜
NA
l ′p ⎠
⎝
(
)
n, p
nn = nn0 = ND
pp = ppp0 = NA
np(-xp)
pn(xn)
np(x)
np’
np0
-lp
p’n
pn0
-xp
l’p
pp
pn(x)
0
xn
ln
l’n
x
Diodo a base corta: correnti di
diffusione dei portatori minoritari
Dai profili dei portatori iniettati si può risalire alle correnti di
diffusione
qD p ni2 VD VT
d
e
−1
j p ( x) = − qD p
pn′ ( x) =
dx
N D ln′
(
)
qDn ni2 VD VT
d
jn ( x) = qDn n′p ( x) =
e
−1
N Al ′p
dx
(
)
Tali correnti non decrescono allontanandosi dalla regione svuotata
ma rimangono ad un valore costante
Questo vuol dire che i portatori minoritari non stanno subendo
alcuna ricombinazione
Diodo a base corta: corrente totale
La densità di corrente totale del diodo è data dalla somma di jp e jn
jD = jn + j p =
⎛ Dn
D p ⎞ VD VT
= qn ⎜
+
e
−1
⎜ N Al ′p N D ln′ ⎟⎟
⎝
⎠
(
2
i
)
VD
A
p
NA
K
n
ND
jD è maggiore
i
rispetto
i
all diodo
di d a
base lunga
W
jn(x)
j
Inoltre si ha
⎧ 2
⎪qni
⎪
jD = ⎨
⎪qn 2
⎪⎩ i
(
)
Dn
eVD VT − 1
N Al ′p
e
(
l′
Dp
ND
VD VT
n
)
−1
se N D >> N A
jn
jp(x)
-lp
-xp
lp’
se N A >> N D
0
xn
jp
ln
ln’
x
Caratteristica I-V
I V del diodo
Moltiplicando la densità di corrente jD per l’area della giunzione AD
è possibile ricavare la corrente elettrica
La relazione corrente
corrente-tensione
tensione per il diodo a base lunga e per il
diodo a base corta è simile e può essere rappresentata da
(
)
I D = I S eVD VT − 1
il termine IS è chiamato corrente inversa di saturazione è pari a
Diodo a base lunga
Diodo a base corta
⎛ Dn
Dp ⎞
I S = AD qn ⎜
+
⎜ N A Ln N D Lp ⎟⎟
⎝
⎠
⎛ Dn
Dp ⎞
I S = AD qn ⎜
+
⎜ N l ′ N l ′ ⎟⎟
D n ⎠
⎝ Ap
2
i
2
i
Caratteristica I-V
I V del diodo
La curva I-V risultante ha un andamento esponenziale nel
semipiano destro e un andamento costante nel semipiano sinistro
Valgono
g
le seguenti
g
approssimazioni
Se VD > 0 e VD > 4VT
I D = I S eVD VT
Se VD < 0 e |VD| > 4VT
ID = −IS
Tensione di soglia
Vγ ≈ 0.7 V
Simbolo circuitale del diodo
A
p
n
NA
ND
A
K
K
Effetti di ricombinazione e di alti
livelli di iniezione
L’equazione corrente-tensione è stata ricavata ipotizzando
1 i portatori non subiscono ricombinazione all
1.
all’interno
interno della
regione di carica spaziale
2. si è in ppresenza di bassi livelli di iniezione
Nella realtà, le suddette ipotesi valgono in modo sufficientemente
accurato
t nell caso di diodi
di di all germanio,
i ma per giunzioni
i i i all silicio
ili i e
all’arsenurio di gallio non risultano sempre adeguate
Analizziamo qualitativamente i due effetti
Effetti dovuti alla ricombinazione
Alcune delle cariche che attraversano la regione svuotata si
ricombinano determinando ai bordi della regione svuotata un
livello dei portatori minoritari che diffondono diverso da quello
previsto
Il fenomeno è dominante per bassi livelli di corrente
Per tenerne conto si introduce un coefficiente n detto coefficiente
di emissione nella relazione I-V
I V del diodo
VD
⎛ nV
⎞
T
I D = I S ⎜ e − 1⎟
⎜
⎟
⎝
⎠
Tale
l coefficiente
ffi i
è compreso tra 1 e 2
Effetti dovuti agli alti livelli di
iniezione
Il fenomeno si presenta per alti livelli di corrente
La corrente che attraversa il diodo presenterà anche una
componente di deriva oltre alla componente di diffusione
Vi sono delle cadute di tensione anche nella regione neutra
Anche in questo caso il coefficiente di emissione permette una
corretta modellistica del diodo
VD
⎛ nV
⎞
T
I D = I S ⎜ e − 1⎟
⎜
⎟
⎝
⎠
Dipendenza dalla temperatura
Dipendendo dalla temperatura sia la tensione termica VT che la
corrente inversa di saturazione IS (funzione di Dn, Dp e ni)
• IS(T) raddoppia ogni 10
10°C
C di temperatura
I S (T ) ≈ 2
T −T0
10
I S (T0 )
• Nell’intorno della temperatura ambiente (T = 300 K) e a corrente
costante la tensione VD diminuisce di circa 2.2
2 2 mV/°C
d VD
mV
≈ −2.2
22
dT
°C
Effetti capacitivi
Descrizione qualitativa degli effetti
capacitivi
• La relazione I-V descrive il diodo a bassa frequenza
• Il legame è di tipo statico (resistore non lineare)
• In un diodo sono presenti degli accumuli di carica che lo
rendono molto simile ad un condensatore
• Ad esempio
esempio, variando istantaneamente la corrente ID la larghezza
della regione svuotata W e la tensione VD non variano
istantaneamente
• È presente una certa inerzia funzione della frequenza del segnale
applicato
Carica nella regione svuotata
La carica per unità di superficie Qj all’interno della regione
svuotata sarà pari a q volte la concentrazione di drogante per la
larghezza della regione
Q j = qN D xn = qN A x p
poiché
NA
xn =
W
ND + N A
2ε s N D + N A
W=
(Vbi − VD )
q ND N A
si ha per Qj
ND N A
Q j = 2qε s
(Vbi − VD )
ND + N A
La dipendenza da VD è non lineare
Capacità di svuotamento
Definiamo la capacità di svuotamento o di giunzione, Cj, come la
variazione della carica ADQj rispetto alla tensione applicata tra il
catodo e l’anodo, ossia –VD
Cj =
dAD Q j
d ( −VD )
=
AD
2 Vbi − VD
ND N A
2qε s
ND + N A
La tensione è valutata tra il catodo e l’anodo in quanto le cariche
positive sono dalla parte del semiconduttore n
Da uun punto
pu o ddi vvista
s ccircuitale
cu e risulta
su u
utilee de
definiree
C j0 =
dQ j
d ( −VD ) V
D =0
qε s N D N A
=
2Vbi N D + N A
da cui
Cj =
C j 0 AD
1 − VD Vbi
Capacità di svuotamento
L’espressione della capacità di svuotamento è stata ricavata per una
giunzione a gradino
Più in generale vale la
seguente formula
Cj =
C j 0 AD
(1 − VD Vbi )
mj
1/3 < m <1/2
m=1/2 giunzione brusca
m=1/3 giunzione lineare
Capacità di svuotamento
Riprendendo l’espressione della capacità di svuotamento
qε s N D N A
1
Cj =
2 N D + N A Vbi − VD
e confrontandola con l’espressione di W
W=
2ε s N D + N A
(Vbi − VD )
q ND N A
è facile verificare che
Cj =
ε s AD
W
che è la relazione di un condensatore lineare con piatti di superficie
AD, distanziati W ed isolati da un dielettrico con costante εs
Carica nella regione neutra
In polarizzazione diretta i profili dei portatori minoritari possono
essere visti come degli accumuli di carica pari a
+∞
− xp
QDn = q
∫
n′p ( x)dx
−∞
QDp = q ∫ pn′ ( x)dx
xn
Nel diodo a base lunga
+∞
QDp = q ∫ pn′ ( x)dx = qL p pn′ ( xn ) ⎡e
⎣
− ( x − xn ) L p
xn
− xp
QDn
( x+ x )
= q ∫ n′p ( x)dx = qLn n′p (− x p ) ⎡e p
⎢⎣
−∞
Ln
+∞
⎤ = qL p pn′ ( xn )
⎦ xn
− xp
⎤ = qL n′ (− x )
n p
p
⎥⎦ −∞
d cuii
da
QDp
D
ni2 VD
= qL p
e
(
ND
VT
− 1)
QDn
D
ni2 VD
= qLn
e
(
NA
VT
− 1)
Carica e corrente
QDp
ni2 VD
= qL p
e
(
ND
VT
− 1)
QDn
ni2 VD
= qLn
e
(
NA
− 1)
VT
confrontando le relazioni con le densità di corrente jp e jn
ni2 VD
jp =
q
e
(
Lp N D
Dp
VT
− 1)
Dn ni2 VD
jn =
q
e
(
Ln N A
VT
− 1)
si ha
jp =
QDp
2
p
L Dp
=
QDp
jn =
τp
da cui
jD = j p + jn =
QDp
τp
+
QDn
τn
QDn
D
2
n
L Dn
=
QDDn
τn
Carica nella regione neutra: diodo a
base corta
Nell diodo
di d a base
b
corta gli
li accumuli
li sono (area
(
del
d l triangolo)
i
l )
+∞
QDp = q ∫
xn
ln′ pn′ ( xn ) ln′ ni2
VD
= q
pn′ ( x))dx = q
e
(
2
2 2ND
− xp
QDn = q
∫
n′p ( x)dx = q
−∞
l ′p n′p (− x p )
2
l ′p
VT
ni2 VD
= q
e
(
2 NA
VT
− 1)
− 1)
Richiamando le densità di corrente
D p ni2 VD
jp =
q
e
(
ln′ N D
si ha
jp =
QDp
ln′ 2 D p
2
VT
− 1)
Dn ni2 VD
jn =
q
e
(
l ′p N A
jn =
QDn
l ′p2 2 Dn
VT
− 1)
Carica corrente e tempi di transito
Carica,
jp =
QDp
jn =
ln′2 2 D p
QDn
l ′p2 2 Dn
Definendo
τ tr , p
ln′2
=
2Dp
τ tr ,n =
l ′p2
2 Dn
quantità che prendono il nome di tempi di transito, si ha
jD =
QDp
τ tr , p
+
QDn
τ tr ,n
I tempi di transito rappresentano il tempo impiegato dai portatori
minoritari ad attraversare la regione neutra
Capacità di diffusione
Gli accumuli di carica nelle regioni neutre creano effetti capacitivi
L carica
La
i totale
t t l da
d considerare
id
è
QD = QDp + QDn
La carica QD è sempre esprimibile nella forma
QD = QD 0 ( eVD
VT
− 1) ≈ QD 0 eVD
VT
Definendo la capacità di diffusione come
dQD
CD = AD
dVD
si ha
QD 0 eVD VT
QD
d
VD VT
CD = AD
QD 0 e
= AD
= AD
dVD
VT
VT
Capacità di diffusione
Nel caso di un diodo p+-n a base lunga, il trasporto di carica è dato
prevalentemente dalle sole lacune e si può scrivere
QD ≈ QDp ≈ τ p j p ≈ τ p jD
Più in generale la carica QD può essere approssimata da
QD ≈
p+-n
p-n+
p
τ n jD
Base lunga τp jD
Base corta τtr,p
t jD τtr,n
t jD
Di conseguenza, per CD si ha
QD
jD AD
ID
CD = AD
≈τ
=τ
VT
VT
VT
dove τ è un tempo opportuno
Tempi di commutazione
Qu do uun ddiodo
Quando
odo vviene
e e portato
po o dalla
d
condizione
co d o e di
d po
polarizzazione
o e
inversa a quella diretta o viceversa, la sua risposta è
accompagnata da una fase transitoria e il raggiungimento dello
stato stazionario si presenta solo dopo un certo intervallo di tempo
Un’analisi dettagliata
g
di qquesti transitori rivela che il tempo
p di
commutazione verso la conduzione è minore rispetto al tempo di
commutazione verso l’interdizione
Risulta pertanto interessante esaminare i due fenomeni anche da un
solo punto di vista qualitativo
Commutazione verso la conduzione
i
Viene detto tempo di turn-on
+
-
vS
Supponendo che Vγ << VF si ha
IF = VF/R
+
+ vD R
vR
-
vS
VF
t
Occorrerà un certo tempo perché la tensione vD
raggiunga il valore finale Vγ
t1
i
Tale tempo è definito come tempo di recupero
diretto ed è indicato con tfr
IF
t
t1
vD
In genere esso è circa due volte il tempo di vita
dei portatori minoritari
Vγ
t
t1
Commutazione verso ll’interdizione
interdizione
i
Viene detto tempo di turn-off
+
-
vS
Quando la tensione passa da VF a VR il diodo
non va immediatamente in interdizione ma deve
prima svuotare la carica QD
QD viene svuotata nell’intervallo ts = t3 – t2
detto tempo di immagazzinamento del diodo
R
ts + tt = trr, tempo
p di recupero
p
inverso
vR
-
vS
VF
t2
t
VR
i
IF
t2
Il tempo oltre t3 necessario per raggiungere il
valore finale è il tempo di transizione,
transizione tt
+
+ vD -
t3
t
IR
vD
Vγ
t2
VR
t3
t
Rottura della giunzione
Tensione di Breakdown
Aumentando la tensione di polarizzazione inversa (VD < 0) esiste
un valore di tensione detta tensione di rottura (o tensione di
breakdown) ed indicata col simbolo BV oltre il quale la corrente
comincia a crescere in modo esponenziale
Due sono le cause di rottura inuna giunzione pn denominate effetto
( rottura)
(o
tt ) valanga
l
edd effetto
ff tt (o
( rottura)
tt ) Zener
Z
Indipendentemente dalla spiegazione fisica del fenomeno,
fenomeno un diodo
che presenta un tale comportamento prende il nome di diodo Zener
A
K
Effetto valanga
L’effetto valanga si verifica quando i portatori liberi a causa
d ll l
dell’elevato
campo elettrico
l i cuii sono soggetti,
i acquistano
i
una
energia cinetica sufficiente da determinare la rottura di un legame
covalente durante le collisioni con gli ioni nel reticolo
Come conseguenza,
g
, pper ogni
g legame
g
covalente rotto si ggenererà
una nuova coppia elettrone-lacuna che a loro volta possono
contribuire al fenomeno
L’effetto è quello di una moltiplicazione esponenziale di portatori
Tale fenomeno si ha per campi dell’ordine di 3·105 V/cm e livelli
di concentrazione di drogaggio
g gg di 1015-1016 atomi/cm3
Rottura Zener
Si manifesta in presenza di alti campi elettrici (nell’ordine di 2·107
V/cm),
/ ) caso frequente
f
nell caso in
i cuii le
l regioni
i i siano
i
fortemente
drogate
L’elevato campo elettrico potrà essere in grado di strappare
alcuni elettroni che formano i legami
g
covalenti,, ggenerando anche in
questo caso nuove coppie elettrone-lacuna che saranno in grado di
partecipare alla conduzione della corrente inversa di saturazione
L’effetto della rottura non sarà quindi dovuto alle collisioni dei
portatori ma sarà causato esclusivamente dalla elevata intensità del
campo
Caratteristica corrente-tensione
corrente tensione
A seconda delle caratteristiche costruttive del diodo prevarrà uno
dei due meccanismi di rottura
Le tensioni di rottura più
basse (< 5 V per diodi al
Si) le
l hanno
h
i diodi
di di add
effetto Zener
Tensione di soglia
g
Vγ ≈ 0.7 V
Tensione di Breakdown
BV ≈ 3.5 V
Dipendenza dalla temperatura
Rottura Valanga
Rottura Zener
All’aumentare della temperatura
sii riduce
id
il libero
lib
cammino
i
medio dei portatori
Aumentando la temperatura
aumenta
t l’energia
l’
i degli
d li elettroni
l tt i
coinvolti in legami covalenti
Gli urti sono più frequenti ma di
minore intensità (libero meno
energia)
Sono necessari campi elettrici
inferiori per strappare gli
elettroni dai loro atomi
La tensione
L
t i
BV aumenta
t con
l’aumento della temperatura
(incremento di circa 0.1%/
0.1%/°C)
C)
La tensione
L
t i
BV diminuisce
di i i
con
l’aumento della temperatura
(incremento di circa –0.1%/°C)
0.1%/ C)
Modellistica della rottura della giunzione
Si introduce un coefficiente M che rappresenta il rapporto tra la
corrente reale in condizioni di rottura IDbr e la corrente prevista
dalle formule IS
M=
I Dbr I Dbr
≈
ID
IS
Vale la seguente relazione empirica
M=
1
1 − (VR BV )
nBV
dove nBV è un coefficiente empirico compreso tra 4 e 6 e
2
ε s Ecrit
3 ⋅ 1017 V ⋅ cm −3
BV =
≈
N
2qN
N è il drogaggio
d
i della
d ll regione
i
meno drogata.
d
Ecrit = 3·105 V/cm
/
Giunzioni metallosemiconduttore: Diodi
Schottky e contatti
ohmici
Diodi Schottky
Una giunzione pn realizza un diodo a semiconduttore mediante la
creazione di una barriera di potenziale che può essere ridotta o
aumentata da una tensione esterna
Tale barriera di potenziale, Vbi, può essere descritta anche dalla
differenza tra i potenziali di contatto intrinseci dei semiconduttori
d
drogati
ti
N A ND
ND
NA
= VT ln
+ VT ln
= Φn − Φ p
Vbi = VT ln
2
ni
ni
ni
U ssimilee risultato
Un
su o ssi può oottenere,
e e e, so
sotto
o
opportune condizioni, anche mediante
contatto tra un metallo e un
semiconduttore
A
n
metallo
x=0
K
ND
x
Creazione della barriera di potenziale
Unendo un metallo e un semiconduttore
debolmente drogato
d
di tipo
i n (N
( D<1016 cm–33)
si ha il passaggio di alcuni elettroni dalla
parte n verso il metallo ossia la creazione di
un potenziale
Vbi
A
densità di
carica
Gli elettroni transitati non creeranno alcuno
ione negativo e corrispondentemente non vi
saràà alcun
l
passaggio
i di lacune
l
dal
d l metallo
ll all
semiconduttore
La regione svuotata si estende solo dal lato
del semiconduttore
n
metallo
K
ND
qND
0
x
xn
xn
0
x
campo
elettrico
potenziale
0
xn
Vbi
x
Definizione del potenziale di barriera
Il potenziale della barriera può essere espresso
mediante differenza dei potenziali di contatto
intrinseci dei materiali
Vbi = Φ n − Φ metallo
Il potenziale
t i l di contatto
t tt intrinseco
i ti
di un
materiale (non necessariamente quindi silicio
drogato) è quel potenziale di contatto che si
viene a creare unendo il materiale in esame e il
silicio intrinseco
Per ogni materiale tale valore sarà una costante
fi i
fisica
Materiale Φ (Volt)
A
Ag
–0.40
0 40
Au
–0.30
Cu
0.00
Ni
N
0.15
0.
5
Al
0.60
Mg
1.35
+
Polisilicio n
0.56
+
P li ili i p
Polisilicio
–0.56
0 56
Si drogato
–φF
Si intrinseco
0.00
Diodi Schottky: caratteristiche
principali
Il trasporto di carica dipende dai portatori maggioritari
Se VD > 0,, il ppotenziale si abbassa e ggli elettroni si spostano
p
dal
semiconduttore al metallo. Viceversa, se VD < 0, la barriera di
potenziale aumenta e interdice il passaggio di cariche
(
)
VD VT
I
=
I
e
−1
La relazione tensione-corrente rimane D S
IS_schottky > IS_pn ovvero Vγ_schottky < Vγ_pn
L’assenza di una carica
L’
i QD rende
d il dispositivo
di
iti più
iù veloce
l
i
in
commutazione
Contatti Ohmici
La giunzione metallo-semiconduttore diventa rettificante e forma
un diodo Schottky solo nel caso in cui il semiconduttore sia
debolmente drogato (ND < 1016 cm–3)
Per alti livelli di drogaggio (ND > 1018 cm–3) il dispositivo presenta
una bassa resistenza al flusso di corrente in entrambe le direzioni
Il passaggio di corrente dal semiconduttore verso il metallo sarà
causato dal cosiddetto effetto tunnel
Il tipo
ti di contatto
t tt che
h sii crea appare come una resistenza
it
di valore
l
molto basso da cui il nome di contatto ohmico
Modelli circuitali
Modelli statici
I modelli statici semplificano l’equazione corrente-tensione
(
)
I D = I S eVD VT − 1
nella
ll quale
l appare uno scomodo
d termine
t
i esponenziale
i l
Essi descrivono il nostro dispositivo come un resistore non lineare
e vengono utilizzati per avere un’analisi veloce ma allo stesso
tempo accurata
La scelta del modello va fatta tenendo conto che la precisione che si
d id ottenere
desidera
tt
è inversamente
i
t proporzionale
i
l allo
ll sforzo
f
computazionale da fare (soprattutto se si lavora con un foglio di
carta ed una penna)
Modello di tipo I
ID
Il diodo è un raddrizzatore puramente ideale
La corrente è nulla per VD < 0 (circuito aperto)
VD
A
La tensione è nulla per ID > 0 (corto circuito)
VD < 0
A
iD
+
-
ID
ID > 0
+
+ vD vS
K
R
vR
t
vR
-
vS
K
Modello di tipo II
ID
Il diodo è un raddrizzatore con soglia
La corrente è nulla per VD < Vγ (circuito aperto)
Vγ
A
VD
K
La tensione è Vγ per ID > 0 (generatore di tensione)
VD < Vγ
Vγ
A
iD
vS
+
-
ID
+
ID > 0
+
+ vD R
Vγ
vR
t
vR
-
vS
K
Modelli di tipo III
e IV
ID
Sono simili ai modelli precedenti
ma introducono una resistenza
che tiene conto della pendenza
finita della transcaratteristica del
di d
diodo
ID
VD
K
A
Vγ
A
K
VD < 0
A ID
VD < Vγ
K
RON
Vγ
A ID +
ID > 0
α=
RON
RON + R
vε = α vS + (1 − α )Vγ
α vS
RON
K
ID > 0
vε
vR
vR
t
vS
VD
t
vS
Analisi di piccolo segnale e modello
per bassa frequenza
Esistono delle applicazioni in cui un diodo è polarizzato per operare
in un p
punto di lavoro ((detto anche p
punto di p
polarizzazione o
quiescent point o bias point) della sua regione di polarizzazione
diretta ed un piccolo segnale tempo variante viene sovrapposto ad
esso
In questa situazione il diodo lavora attorno a questo punto fisso
Il diodo viene descritto da una conduttanza uguale
g
alla p
pendenza
della tangente geometrica passante per il punto di lavoro della
caratteristica corrente-tensione
Convenzioni usate nell
nell’analisi
analisi di
piccolo segnale
Le variabili valutate nel punto di lavoro (Q) sono
VD , I D
indicate con lettere e pedici maiuscoli
Le grandezze tempo varianti o di piccolo segnale
sovrapposte al punto di lavoro sono indicate con
lettere e pedici minuscoli
vd ( t ) , id ( t )
La somma tra la grandezza valutata in
polarizzazione ed il piccolo segnale viene indicato vD ( t ) , iD ( t )
con lettere
l tt
minuscole
i
l e pedici
di i maiuscoli
i
li
iD ( t ) = I D + id ( t )
vD ( t ) = VD + vd ( t )
Analisi di piccolo segnale
Il diodo viene mantenuto in un
determinato punto di lavoro, Q,
grazie ad un generatore di
t i
tensione
VD edd un segnale
l
tempo variante vd (triangolare
nell’esempio)
nell
esempio) viene ad esso
sovrapposto
iD
(mA)
tangente in Q
pendenza = gD
1.5
punto di
polarizzazione
ID
Q
1.0
t
0.5
id(t)
iD(t)
VD
vd(t)
+
VD
-
+
-
+
0
0.55
0.60
0.65
0.70
0.75
vD(t)
vd(t)
t
0.80
vD (V)
Analisi di piccolo segnale
In assenza del segnale vd, la tensione ai capi del diodo è VD e la sua
corrente di polarizzazione è
I D = I S eVD VT
Quando viene sovrapposto il segnale vd, la tensione istantanea del
diodo è vD e la corrente istantanea iD risulta essere
iD = I S evD VT = I S e(
VD + vd ) VT
= I S eVD VT evd
VT
= I D evd
VT
Se il segnale vd è molto piccolo (circa 10 mV), è possibile
sviluppare in serie di Taylor l’esponenziale ottenendo
⎛ v
iD ≈ I D ⎜1 + d
⎝ VT
⎞
ID
=
+
I
vd
⎟ D
VT
⎠
Analisi di piccolo segnale
⎛ vd
Confrontando iD ≈ I D ⎜1 +
⎝ VT
⎞
ID
⎟ = I D + vd
VT
⎠
con iD = I D + id
osserviamo che abbiamo espresso la corrente iD come somma di
una componente continua pari alla corrente di polarizzazione e
funzione della sola VD, e di una componente tempo variante
f i
funzione
della
d ll sola
l vd
Definendo
gD =
1 ID
=
rD VT
otteniamo
id = g D ⋅ vd =
1
⋅ vd
rD
Conduttanza di
piccolo segnale
p
g
La formula di Taylor e gD
Un simile risultato si poteva ottenere applicando direttamente lo
sviluppo in serie di Taylor all’equazione corrente-tensione
Dif tti sii ha
Difatti,
h la
l seguente
t analogia
l i
⎡ df ( x ) ⎤
f ( x ) − f ( x0 ) ≈ ⎢
⋅ ( x − x0 )
⎥
⎣ dx ⎦ x = x0
⎡ diD ⎤
iD − I D ≈ ⎢
⋅ ( vD − VD )
⎥
⎣ dvD ⎦ vD =VD
lla quale
l consente
t di ricavare
i
la
l
relazione più generale per gD
⎡d
diiD ⎤
gD = ⎢
⎥
d
v
⎣ D ⎦ vD =VD
Poiché vD=VD equivale a dire nel
punto di lavoro,, sono comuni
p
anche le seguenti definizioni per gD
⎡ di ⎤
⎡ di ⎤
gD = ⎢ D ⎥
=⎢ D ⎥
⎣ dvD ⎦ iD = I D ⎣ dvD ⎦ Q
Significato geometrico di gD
iD
(mA)
Alla luce di ciò, appare
evidente l’interpretazione
grafica che viene data alla
conduttanza gD
Essa rappresenta la pendenza
della tangente geometrica alla
caratteristica corrente-tensione
del diodo nel punto Q
tangente in Q
pendenza = gD
1.5
punto di
polarizzazione
ID
Q
1.0
t
0.5
id(t)
VD
0
0.55
0.60
0.65
0.70
0.75
vd(t)
t
0.80
vD (V)
Esempio di analisi
iD = ID + id
1) Trovare il punto di lavoro
vs
Sostituire al diodo il modello statico di
tipo II (Vγ = 0.7 V) e ricavare il punto di
lavoro del diodo
VD = Vγ
ID =
2) Valutare i parametri di piccolo
segnale
l del
d l dispositivo
di
iti attorno
tt
all punto
t
di lavoro
+
-
+
vD = V D + vd
+
VDD
-
-
R
ID
VDD − Vγ
R
R
+
Vγ
+
VDD
-
VD
-
id
R
+
Calcolare la resistenza del diodo rD come
rd =
VT
VT
=R
ID
VDD − Vγ
vs
+
-
rd
vd
-
Esempio di analisi
3) Trovare le restanti grandezze di
piccolo segnale
iD = ID + id
vs
R
+
-
+
vD = V D + vd
+
VDD
-
Calcolare la tensione e la corrente ai capi
del diodo come
vd =
rd
vs
R + rd
id =
vs
R + rd
-
R
ID
+
Vγ
+
VDD
-
VD
-
4) Completare l’analisi sommando alle
grandezze del punto di lavoro quelle
trovate per piccolo segnale
id
R
+
vs
+
-
rd
vd
-
Modello di piccolo segnale ad alta
frequenza
Polarizzazione diretta
1 VT
rD =
=
gD ID
Cj =
C j 0 AD
(1 − VD Vbi )
CD = τ g D
mj
≈ 2C j 0 AD
id
+
rD
vd
CD
-
Polarizzazione inversa
Cj =
+
C j 0 AD
(1 − VD
Vbi )
mj
id
Cj
vd
-
Cj