Lezione 7 I e II Prinicipio

Lezione 7
I e II Prinicipio
Lavoro:
W =
Z
Serway,
17
Cap.
Serway,
17.4
Cap.
pdV
se la pressione é costante:
W = p∆V
Unitá di misura:
1litro = 10−3 m3
1atm ' 1.013105 P a = 1.013105 N m−2
quindi: litro atm ' 101.3Joule
7.1
7.1.1
lavoro ed energia termica
XVII. 18
Un gas in un contenitore é alla pressione di 1.5 atm e occupa un volume di
4.0 m3 . Qual’é il lavoro fatto dal gas se si espande a pressione costante ad un
volume doppio? E se é compresso a pressione costante ad un quarto del suo
volume iniziale?
Soluzione:
Vi = 4.m3 → Vf = 8.0m3
quindi, essendo la pressione costante:
W = p∆V = 1.5atm × (8. − 4.)m3
Essendo ∆V > 0 il lavoro é positivo (é fatto dal gas sul sistema) Ricordando
che 1atm ' 1.013 × 105 P a = 1.013 × 105 N m−2 si ha:
W = 1.5 × 1.013 × 105 N m−2 (8. − 4.)m3 = 607.8kJ
1
Per la compresione:
Vi = 4.m3 → Vf = 1.m3
W = 1.5 × 1.013 × 105 N m−2 (1. − 4.)m3 = −455.850kJ
7.1.2
22
Un campione di elio si comporta come un gas ideale quando viene riscaldato a
pressione costante da 273 K a 373 K. Se il gas compie 20 J di lavoro, qual’é la
massa dell’elio?
essendo costante la pressione,
W = p∆V = pVf − pVi
ma, essendo il gas ideale
pV = nRT
quindi:
W = nR(Tf − Ti ) = nR∆T
ne segue che
W
20J
=
R∆T
R100K
Ricordando che R = 8.31J mole−1 K −1 si ha:
n=
n=
20J
= 0.024mol
8.31J mole−1 K −1 100K
quindi il gas consiste di n = 0.024 moli. Poiché il peso molecolare dell’elio é
m = 4g/mole una mole di elio pesa (ossia: “ha massa”) Mmole = 4.00g e quindi
n moli hanno massa:
M = Mmole n = 4.00 × .024 = .096gr
7.2
7.2.1
I principio e sue applicazioni
XVII.23
Si comprime un gas alla pressione costante di 0.8 atm, da un volume di 9. litri
a un volume di 2 litri. Nel processo, 400 J di energia termica sono ceduti al gas;
Qual’é il lavoro compiuto dal gas? Qual’é la variazione di eneriga interna?
soluzione:
il lavoro (poiché la pressione é costante) é trasformando i litri atm in Joule
si ha:
W = p∆V = (2 − 9)0.8litri atm = −7 × 0.8 × 1.013102 N m−2 = −568.400J
Il primo principio:
∆U = Q − W = −400J + 568.400J = 168.400J
2
7.2.2
24.XVII
Un sistema termodinamico subisce una trasformazione durante la quale l’eneria
interna diminusice di 500 J. Se allo staesso tempo si compione 220 J di lavoro
sul sistema, trova il calore assorbito o ceduto dal sistema.
Secondo le convenzioni,
∆U = −500J < 0
W = +220J > 0
Poiché
∆U = Q − W
si ha:
Q = ∆U + W = −500J + 220J = −280J
Essendo Q negativo, il calore é ceduto dal sistema.
7.2.3
28
Una mole di gas perfetto compie 3000 J di lavoro sull’ambiente circostante
mentre si espande isotermicamente fino a una pressione finale di 1 atm e a un
volume finale di 25 litri. determina il volume iniziale e la temperatura (costante)
del gas. Poiché la trasformazione é isoterma, P V é costante e uguale a RT
(abbiamo una sola mole: n = 1),
P =
RT
V
ma la pressione P non é costante, e dunque il lavoro fatto va calcolato integrando:
Z Vf
Z Vf
Vf
RT
W =
pdV =
dV = RT (log Vf − log Vi ) = RT log
V
Vi
Vi
Vi
(osserviamo che tale espressione vale se la temperatura é costante, e se il gas
é perfetto.)
30.
Una mole di gas inizialmente alla pressione di 2 atm e al volume di 0.3 litri
ha un’energia interna pari a 91 J. Nel suo stato finale, la pressione é di 1.50
atm, il volume 0.8 litri e l’energia interna é uguale a 182 J. Per i tre cammini
in figura (P17.30) calcolare: (a) il lavoro compiuto dal gas e l’energia termica
netta scambiata nella trasformazione.
Soluzione:
R
il lavoro compiuto dal gas é dato da pdV ed é (quindi) uguale all’area sotto
la curva p = p(V ). Tale area cambia per i tre percorsi. L’energia interna cambia
di
∆U = Uf − Ui = 182J − 91J = 91J
3
Serway 17.6
e il calore scambiato é, secondo il primo principio:
Q = ∆U + W
1.
W1 = pf ∆V = 1.50atm × (0.8 − 0.3)litri
si ha:
W1 = 0.5 × 1.5 × 101.3J = 75.975
(fatto dal gas) e quindi, per il primo principio: 91J = Q − 75.97J quindi:
Q1 = 91 + 75 = 166
Poiché il calore é positivo, esso é assorbito dal gas
2.
W2 = pi ∆V = 2atm × (0.8 − 0.3)litri
W2 = 2 × 0.5 × 101.3J = 101.3J
(l’espansione avviene ad una pressione maggiore, quindi il lavoro fatto dal
gas é maggiore)
Q2 = 91 + 303.90 = 394.90J
3. L’area sottesa é l’unione di un triangolo e di un rettangolo.
W3 =
∆V ∆p
+W1 = 0.5×(0.8−0.3)×(2−1.5)×101.3+W1 = 12.6625+W1 = 88.635J
2
Q3 = 91 + 88.63 = 179.63
47.
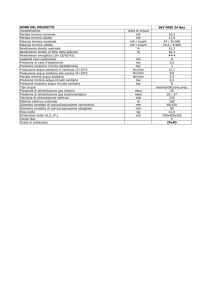
Un gas perfetto é inizialmente a pressione P0 , volume V0 e temperature T0 ,
descrive il ciclo di figura P17.47; trova il lavoro complessivo fatto dal gas nel
ciclo. quanto é il calore complessivo assorbito dal sistema per ciclo? ottenere
un valore numerico per tale lavoro per una mole di gas inizialmente a T0 = 0C◦ .
Il lavoro svolto é l’area conchiusa dal ciclo. Nel nostro caso
W = 2P0 × 2V0 = 4P0 V0
Per il primo principio,
∆U = Q − W
ma, poich il sistema torna allo stato iniziale, l’energia interna non cambia (∆U =
0) e dunque
Q = W = 4P0 V0
Poiché il gas é perfetto, P V = nRT . per una sola mole, a T = 0C◦ si ha:
P0 V0 = RT =
4
7.3
II Principio
Rendimento (definizione):
e = W/Qc = 1 − Qf /Qc
Rendimento della macchina di Carnot:
eC = 1 − Tf /Tc
7.4
Macchine termiche
2. Rendimento
Una macchina termica produce 200 J di lavoro in ogni ciclo e ha un rendimento
pari al 30.0%. Per ciascun ciclo, quanta energia termica viene assorbita, e quanto
ceduta?
Poiché ∆U = 0 il primo principio da: W = (Qc − Qf ); inoltre, il rendimento
é per definizione: e = W/Qc quindi:
Qc = W/e =
200J
= 666.66J
0.3
da cui:
Qf = −W + Qc = −200 + 666.66 = 466.66J
4. Rendimento della macchina di Carnot
Una macchina termica lavora tra 200 ◦ C e 80 ◦ C raggiungendo il 20 % del
rendimento massimo possibile. Quanto calore deve essere assorbito affinché la
macchina compia 10 kJ di lavoro?
Il rendimento massimo possibile é quello della macchina di Carnot: eC =
1 − Tf /Tc e quindi, per la macchina in questione é:
eC = 1 −
80◦ C
= .60 = 60%
200◦ C
quindi la macchina reale ha rendimento:
e = 20% × 60% = .12 = 12%
dalla definizione di rendimento si ha:
Qc =
10kJ
W
=
= 83333.33kJ
e
.12
5
10. Rendimento della macchina di Carnot
Una centrale lavoro con un rendimento del 32% durante l’estate quando l’acqua
del mare per il raffreddamento é a 20◦ C. La centrale usa vapore a 350 ◦ C per
far funzionare le turbine. Assumento che il rendimento reale vari con la stessa
proporzione del rendimento ideale, quale sarebbe il rendimento della centrale in
inverno quando l’acqua del mare é a 10. ◦ C?
Consideriamo una macchina di Carnot ideale, che lavori alle temperature di
esercizio della centrale: in estate il suo rendimento é:
eEstate
=1−
C
TfEstate
20◦ C
= .94 = 94%
=1−
TC
350◦ C
in inverno, invece:
=1−
eInverno
C
TfInverno
10◦ C
= .97 = 97%
=1−
TC
350◦ C
il rendimento reale in estate é, secondo il testo eEstate = 32% e, sempre
secondo il tetso, vale
eEstate
eEstate
C
= Inverno
Inverno
e
eC
da cui:
eInverno =
eInverno
97%
C
× eEstate =
× 32% ' 33%
Estate
94%
eC
6