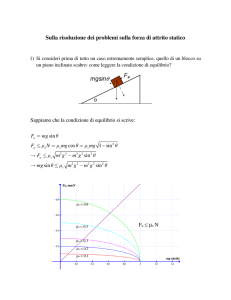
Cinematica e Dinamica
1. Un blocco di massa m che scivola lungo un tavolo privo di attrito è fissato a un filo che passa per un
piccolo foro al centro del tavolo. Il blocco percorre con velocità vo una traiettoria circolare di raggio ro.
Determinare (a) la tensione del filo, (b) il momento angolare. Un ragazzo sotto il tavolo tira lentamente il
filo verso il basso. Quale sarà la velocità quando il raggio della traiettoria circolare sarà ro/2.
2. Un giocatore di freccette è posto a una distanza d = 2.37 m dal bersaglio che vuole colpire e lancia verso
il centro del bersaglio, da una quota iniziale pari a quella del centro del bersaglio, una freccetta alla
velocità v0 = 12 m/s. Sapendo che il diametro del bersaglio è h = 0.453m, dire se il giocatore colpirà o
meno il bersaglio.
3. Il blocco A ha massa pari a mA= 4.4 kg. I coefficienti di attrito statico e
dinamico tra il blocco A ed il tavolo sono rispettivamente µS = 0.18 e
µD = 0.15. Determinare: a) la minima massa mB del blocco B che fa
scivolare il blocco A, b) l’accelerazione di A quando la massa mB e
quella calcolata nel punto a) e il sistema è in moto, c) la tensione del
filo TF nel caso statico e dinamico, quando la massa mB e quella
calcolata nel punto a).
4. Un blocco P descrive un moto armonico semplice, di frequenza 1,5 Hz, scivolando lungo una superficie
priva d’attrito orizzontale. Un blocco B è in quiete, come viene mostrato in figura. Il coefficiente d’attrito
statico tra i due blocchi è 0,6. Calcolare le seguenti quantità:
i. la massima ampiezza di oscillazione del sistema costituito dai due blocchi, senza che B scivoli su P.
B
P
5.
6.
6.
Un pendolo semplice è composto da un filo inestensibile e di massa trascurabile di lunghezza L = 60 cm
e da una massa puntiforme M = 400 g. Si sa che il filo si spezza se sottoposto tensioni uguali o maggiori
di Tmax = 5.0 N.
A. Determinare l’angolo minimo αmin (rispetto alla posizione di riposo) da cui fare partire l’oscillazione del
pendolo perché il filo si spezzi durante il moto.
B. Determinare a quale distanza (orizzontale) dalla posizione a riposo cade a terra la massa nella caduta che
consegue alla rottura del filo di cui al punto a), sapendo che il filo è agganciato ad un’altezza 3L dal
terreno.
7.
8.
9. Un punto materiale si muove di moto oscillatorio sotto l’azione combinata di una forzante periodica, di una
forza elastica e una forza di attrito viscoso. Scrivere l’equazione dinamica del moto. Spiegare: i) di cosa
dipende il periodo di oscillazione del punto materiale, ii) in quali condizioni si verifica il fenomeno di
risonanza.
10. Un blocco di massa m che scivola lungo un tavolo privo di attrito è fissato a un filo che passa per un piccolo
foro al centro del tavolo. Il blocco percorre con velocità vo una traiettoria circolare di raggio ro. Determinare
(a) la tensione del filo, (b) il momento angolare e (c) l’energia cinetica del blocco. Un ragazzo sotto il tavolo
tira lentamente il filo verso il basso. Quanto lavoro deve compiere per ridurre il raggio della traiettoria
circolare fino al valore ro/2.
11. Un oggetto di massa m viene lanciato con velocità v lungo un piano scabro (coefficienti d’attrito statico µs
e dinamico µd) inclinato verso l’alto di un angolo α. Si calcoli:
A. il valore di µd affinché l’oggetto si arresti ad una quota h’= v 2/(3g) dal punto iniziale;
B. supponendo che µs = 1.5 µd, si stabilisca se l’oggetto resterà fermo nella posizione raggiunta oppure
scivolerà indietro verso il punto di partenza.
12.