forze, lavoro, energia – esercizio n. 14
Il cavo di un ascensore di massa 1500 kg si spezza quando l’ascensore è fermo ad
una distanza d = 5 m da una molla di costante elastica k = 11,7·104 N/m.
Un dispositivo di sicurezza agisce sulle guide in modo da sviluppare una forza di
attrito costante di 9000 N, che si oppone al moto dell’ascensore.
Calcolare:
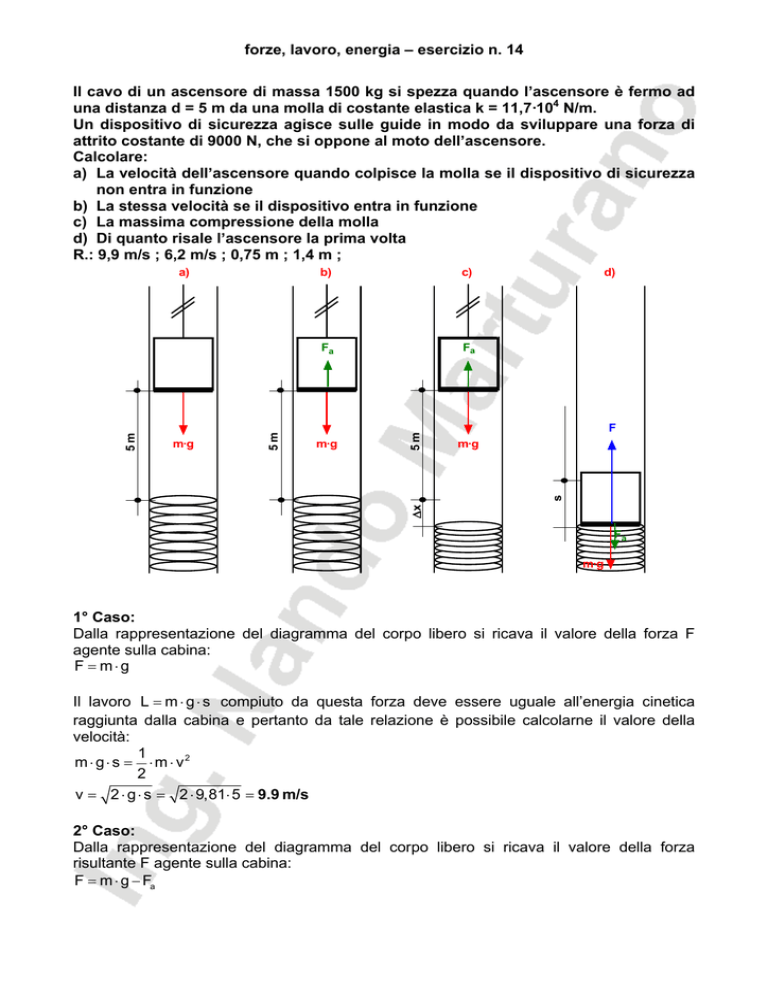
a) La velocità dell’ascensore quando colpisce la molla se il dispositivo di sicurezza
non entra in funzione
b) La stessa velocità se il dispositivo entra in funzione
c) La massima compressione della molla
d) Di quanto risale l’ascensore la prima volta
R.: 9,9 m/s ; 6,2 m/s ; 0,75 m ; 1,4 m ;
b)
c)
Fa
Fa
d)
F
m·g
∆x
s
m·g
5m
m·g
5m
5m
a)
Fa
m·g
1° Caso:
Dalla rappresentazione del diagramma del corpo libero si ricava il valore della forza F
agente sulla cabina:
F = m⋅g
Il lavoro L = m ⋅ g ⋅ s compiuto da questa forza deve essere uguale all’energia cinetica
raggiunta dalla cabina e pertanto da tale relazione è possibile calcolarne il valore della
velocità:
1
m ⋅ g ⋅ s = ⋅ m ⋅ v2
2
v = 2 ⋅ g ⋅ s = 2 ⋅ 9,81⋅ 5 = 9.9 m/s
2° Caso:
Dalla rappresentazione del diagramma del corpo libero si ricava il valore della forza
risultante F agente sulla cabina:
F = m ⋅ g − Fa
forze, lavoro, energia – esercizio n. 14
Il lavoro
L = ( m ⋅ g − Fa ) ⋅ s
compiuto da questa forza deve essere uguale all’energia
cinetica raggiunta dalla cabina e pertanto da tale relazione è possibile calcolarne il valore
della velocità:
1
(m ⋅ g − Fa ) ⋅ s = ⋅ m ⋅ v 2
2
2 ⋅ ( m ⋅ g − Fa ) ⋅ s
v=
m
=
2 ⋅ (1500 ⋅ 9,81 − 9000 ) ⋅ 5
1500
= 6,2 m/s
3° Caso:
Dalla rappresentazione del diagramma del corpo libero si ricava il valore della forza
risultante F agente sulla cabina:
F = m ⋅ g − Fa = 1500 ⋅ 9,81 − 9000 = 5715 N
La massa della cabina dell’ascensore, sotto l’azione della forza F si sposterà di (s + ∆x )
(dove ∆x rappresenta l’accorciamento della molla) per cui il lavoro ∆L compiuto,
equivalente all’energia cinetica acquisita dalla massa m), si trasformerà, per il principio di
conservazione dell’energia meccanica, in energia potenziale elastica di compressione
della molla che si accorcerà del tratto ∆x.
1
(m ⋅ g − Fa ) ⋅ ( s + ∆x ) = ⋅ k ⋅ ∆x 2
2
5715 ⋅ ( 5 + ∆x ) = 0,5 ⋅ 11,7 ⋅ 10 4 ⋅ ∆x 2
11,4 ⋅ 103 ⋅ ( 5 + ∆x ) = 117 ⋅ 103 ⋅ ∆x 2
117 ⋅ ∆x 2 − 11,4 ⋅ ∆x − 57 = 0
⋅∆x =
5,7 ± 32,5 + 6669 5,7 ± 81,8
=
117
117
→
∆x1 = 0,75
∆x 2 = −0,65
Ovviamente viene scartata la soluzione negativa, per cui:
∆x = 0,75 m
4° Caso:
Dalla rappresentazione del diagramma del corpo libero si ricava il valore della forza
risultante F agente sulla cabina:
F = m ⋅ g + Fa = 1500 ⋅ 9,81 + 9000 = 23715 N
L’energia potenziale elastica di compressione della molla vale:
1
∆U = ⋅ k ⋅ ∆x 2 = 0,5 ⋅ 117 ⋅ 103 ⋅ 0,752 = 32906 N
2
Questa energia provvederà a compiere il lavoro ∆L necessario a far risalire la massa m:
∆U = ∆L
dove:
∆L = F ⋅ s
da cui:
s=
∆U 32906
=
= 1,4 m
F
23715












