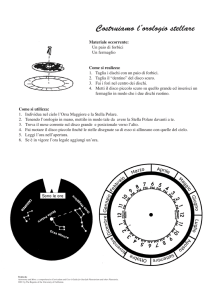
XXIII
ETNIADE
MATEMATICA
14 aprile 2014
I risultati saranno pubblicati sul sito
http://www.dmi.unict.it/etniade/
1. Per quale valore di n è vera la seguente eguaglianza?
1
1
1
(1 + ) ∙ (1 + ) ∙ … ∙ (1 + ) = 2014
2
3
n
2. Il quadrilatero convesso ABCD ha un angolo retto in A, inoltre le misure dei suoi lati sono ̅̅̅̅
AB = 4,
̅̅̅̅ = 6, CD
̅̅̅̅ = 7, DA
̅̅̅̅ = 3. Quanto vale la sua area?
BC
52,0 °
3. Alla precedente Etniade
hanno partecipato 378 studenti di 1° e 2° anno. Il numero di studenti del 1°
anno è pari all’80% del numero degli studenti del 2° anno. Quanti studenti del 1° anno hanno
A
partecipato all’Etniade?
4. La punta di freccia ABGC è stata ottenuta disegnando un triangolo ABC
rettangolo in A, con ̅̅̅̅
AB = ̅̅̅̅
AC = 2, e il suo baricentro G. Quanto vale l’area
D
ricoperta dalla punta di freccia?
C
G
B
C
5. Quante sono le coppie ordinate (x,y), con x e y interi positivi, soluzioni dell’equazione
x2 + 2y2 = 4xy ?
A
K
B
6. Si consideri una sfera di raggio 2 e tre piani, a due a due fra loro ortogonali, passanti per il centro
della sfera. I tre piani intersecano la superficie s della sfera in tre circonferenze che suddividono s in
triangoli a contorno curvilineo tra loro uguali. Quanto vale il perimetro di uno dei suddetti triangoli?
7. Alberto gioca con due dadi non truccati, uno a forma di tetraedro regolare, sulle cui facce sono
segnati i numeri 1, 2, 3, 4 e uno a forma di cubo, sulle cui facce sono segnati i numeri 0, 0, 1, 2, 3, 4.
Qual è la probabilità che lanciando i due dadi il prodotto dei numeri usciti sia maggiore di 8?
8. Hai a disposizione tre pioli A, B, C. Nel piolo A trovi tre dischi di differente
diametro disposti in modo che ogni disco soprastante è più piccolo del disco
sottostante. Puoi effettuare solo lo spostamento, da un piolo ad un altro, del disco
superiore di un piolo. Non puoi però mettere un disco più grande sopra un disco
più piccolo. Qual è il minimo numero di spostamenti da effettuare per ricostruire
la configurazione iniziale nel piolo C?
9. L’angolo in A del quadrilatero convesso ABCD misura 52° e C è il simmetrico del circocentro del
triangolo ABD rispetto alla retta BD. Quanti gradi misura l’angolo in C?
10. Piero si diverte a scrivere su ogni pagina del suo libro di matematica un numero utilizzando la
seguente regola: sulla prima pagina scrive un numero, che indichiamo con n1, sulla seconda pagina
scrive un numero, che indichiamo con n2, sulla terza pagina scrive la differenza tra n2 e n1, che
indichiamo con n3, e così via a pagina k scrive il numero nk = nk1 nk2. Se n1 = 4 e n2 =2, cosa scrive
a pagina 2014?