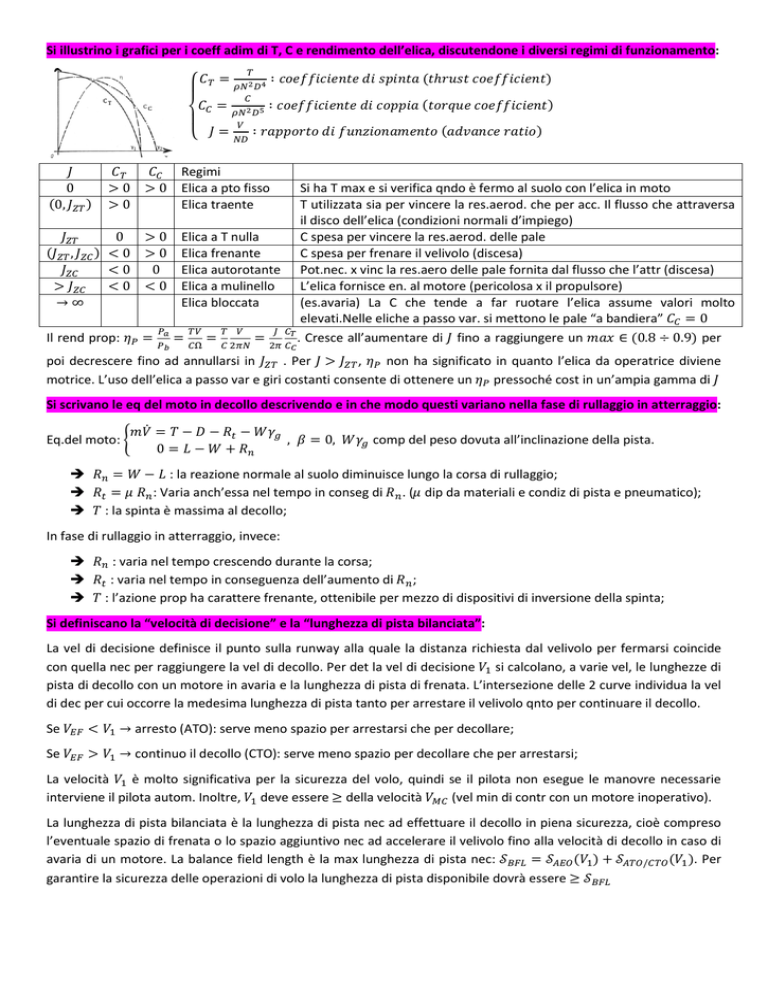
Si illustrino i grafici per i coeff adim di T, C e rendimento dell’elica, discutendone i diversi regimi di funzionamento:
Regimi
Elica a pto fisso
Elica traente
Elica a T nulla
Elica frenante
Elica autorotante
Elica a mulinello
Elica bloccata
Il rend prop:
Si ha T max e si verifica qndo è fermo al suolo con l’elica in moto
T utilizzata sia per vincere la res.aerod. che per acc. Il flusso che attraversa
il disco dell’elica (condizioni normali d’impiego)
C spesa per vincere la res.aerod. delle pale
C spesa per frenare il velivolo (discesa)
Pot.nec. x vinc la res.aero delle pale fornita dal flusso che l’attr (discesa)
L’elica fornisce en. al motore (pericolosa x il propulsore)
(es.avaria) La C che tende a far ruotare l’elica assume valori molto
elevati.Nelle eliche a passo var. si mettono le pale “a bandiera”
. Cresce all’aumentare di fino a raggiungere un
per
poi decrescere fino ad annullarsi in
. Per
,
non ha significato in quanto l’elica da operatrice diviene
motrice. L’uso dell’elica a passo var e giri costanti consente di ottenere un pressoché cost in un’ampia gamma di
Si scrivano le eq del moto in decollo descrivendo e in che modo questi variano nella fase di rullaggio in atterraggio:
Eq.del moto:
comp del peso dovuta all’inclinazione della pista.
: la reazione normale al suolo diminuisce lungo la corsa di rullaggio;
: Varia anch’essa nel tempo in conseg di . ( dip da materiali e condiz di pista e pneumatico);
: la spinta è massima al decollo;
In fase di rullaggio in atterraggio, invece:
: varia nel tempo crescendo durante la corsa;
: varia nel tempo in conseguenza dell’aumento di ;
: l’azione prop ha carattere frenante, ottenibile per mezzo di dispositivi di inversione della spinta;
Si definiscano la “velocità di decisione” e la “lunghezza di pista bilanciata”:
La vel di decisione definisce il punto sulla runway alla quale la distanza richiesta dal velivolo per fermarsi coincide
con quella nec per raggiungere la vel di decollo. Per det la vel di decisione si calcolano, a varie vel, le lunghezze di
pista di decollo con un motore in avaria e la lunghezza di pista di frenata. L’intersezione delle 2 curve individua la vel
di dec per cui occorre la medesima lunghezza di pista tanto per arrestare il velivolo qnto per continuare il decollo.
Se
arresto (ATO): serve meno spazio per arrestarsi che per decollare;
Se
continuo il decollo (CTO): serve meno spazio per decollare che per arrestarsi;
La velocità
è molto significativa per la sicurezza del volo, quindi se il pilota non esegue le manovre necessarie
interviene il pilota autom. Inoltre, deve essere della velocità
(vel min di contr con un motore inoperativo).
La lunghezza di pista bilanciata è la lunghezza di pista nec ad effettuare il decollo in piena sicurezza, cioè compreso
l’eventuale spazio di frenata o lo spazio aggiuntivo nec ad accelerare il velivolo fino alla velocità di decollo in caso di
avaria di un motore. La balance field length è la max lunghezza di pista nec:
. Per
garantire la sicurezza delle operazioni di volo la lunghezza di pista disponibile dovrà essere
Si dimostri l’effetto stab dell’imp orizz, evidenziando le grand con le qli è poss aumentare o diminuire tale effetto:
Lo stab è una sup fissa posta a poppavia dell’ala, opp calettata, detto anche imp orizz. L’effetto portante di questa
sup fornisce l’essenziale contributo stab. Infatti, assumendo che
e
sviluppati dall’impennaggio dipendano
linearmente dall’incidenza di volo:
. Con la regola del trasp dei mom possiamo
scrivere il contributo dell’impennaggio al mom di beccheggio baricentrale dell’intero velivolo come:
e derivando rispetto ad
, il contributo
:
(descrive l’effetto stab della sup). Essendo
è negativo (ossia stab) se:
(
si trova dietro
). Dato che il centro di
massa del velivolo si trova in prossimità dell’ala, la condiz precedente è soddisfatta ponendo lo stab a poppavia
dell’ala. L’effetto stab sarà dunque maggiore qnto maggiori saranno il braccio
e/o il valore della
pendenza della curva di portanza dello stab
Sist di rif solidale, aerod, angoli
.
e , la vel di volo mediante tali angoli e la mat dei coseni direttori:
Il sist di rif assi corpo ha origine nel pto mat del velivolo ed assi ortogonali
con il piano di simm mat del velivolo. In particolare:
-
t.c. il piano
coincida
: asse di rollio (allineato con l’asse longitudinale della fusoliera);
: asse di beccheggio (diretto verso la semiala destra);
: asse di imbardata (rivolto verso il basso del velivolo).
Vel di volo:
Il sist di rif assi vento ha origine in un pto mat
-
del velivolo ed assi ortonormali
: è allineato con la velocità di volo;
: è contenuto nel piano di simm del velivolo, disposto in modo da formare un ang acuto con l’asse
.
La vel di volo nel sistema assi vento:
(
):
1) Rotazione di
2) Rotazione di
attorno a ;
attorno all’asse z ottenuto (che coincide con
);
Qndi la mat dei coseni direttori:
Si scrivano le eq di eq in virata corr, ricav R e T in funz di n; diag di prestazioni in T/D e limitazioni connesse:
Assumendo che il volo sia simm (
), unif (
) e staz (
) e che
e
le eq di eq
della virata corretta stazionaria sono:
Dalla 2° eq, sostituendo
.Da
, sapendo che
, ricavo:
Consideriamo i diagr di Penaud in virata correta: si può osservare che per
fissati, le curve di resistenza
formano usa schiera analoga a qlla che si ottiene in volo livellato al variare del peso. Infatti la sola diff tra le eq in
virata e qlle in LF sta nella sostituzione di con il suo peso apparente
. Mancano grafici
Prob dell’eq e della stab stat long per un’ala isolata. Dim effetto stab dell’imp orizz e grand sulle quali è poss agire:
Consideriamo un velivolo costituito da un’ala isolata in LF
forma adima:
. Supponendo che
mom:
e
, essendo:
le eq di eq in
dell’ala Є all’asse di rollio applichiamo la regola del trasp dei
, ma per l’eq di centraggio:
(impone che G si trovi ad una det dist
da A). Essendo
cost (dip essenzialmente dalla forma dell’ala), la dist tra e dip da
e quindi al
variare di questi dovrà cambiare la posiz di , cosa irrealizzabile nella maggior parte dei velivolo. Per ottenere una
variazione di
e quindi della geom dell’ala, si introduce un flap la cui deflessione sia controllabile con continuità
(equilibratore). Essendo in prossimità dell’ala, maggiore sarà la dist dell’equilibratore dall’ala, minore sarà la forza
nec per creare una variazione di momento, e quindi minore la sup e/o la deflessione dell’equil. Se ora imponiamo la
condizione di stab statica:
e dato che per l’ala isolata
. L’equil è
stabile solo se
-
. Consideriamo profili a singola curvatura:
Profili convessi :
Profili simmetrici :
Profili concavi :
;
;
.
Le ali dotate di buone prestazioni aerod sono quelle composte da profili convessi e pertanto instabili. Profili a doppia
curvatura risultano svantaggiosi dal punto di vista aerodinamico. Scartata la possibilità di ottenere un’ala isolata stat
stabile, rimane la possibilità di aggiungere al velivolo una seconda sup portante, lo stab orizz. L’effetto portante di
questa sup fornisce l’essenziale contributo stab.
Infatti, assumendo che:
, la regola del trasp consente di scrivere il contributo
dell’impennaggio al mom di beccheggio baricentrale dell’intero velivolo come:
derivando rispetto ad :
e
(descrive l’effetto stab della superficie). Essendo
, qsto
contributo è stab (ossia negativo) se:
(
si trova dietro a ). L’effetto stab sarà dunque maggiore
quanto maggiori saranno i valori del braccio e/o della pendenza della curva di portanza dello stabilizzatore.
Si mostri come calc
e
x centrare il vel ad un dato coeff di portanza tot. :
Il sistema di forze aerodinamiche agenti sul velivolo può essere inteso come un sistema composto dalle sole forze:
. Le leggi costit in forma omog:
e qndi la portanza e il mom di becch tot dell’intero velivolo possono essere
scritti:
. Utilizzando qste espress nelle eq di eq per risolvere il probl del
trimmaggio, otteniamo:
Quindi, dalle definizioni di
e risolvendo qsto sist:
e
è possibile ottenere
e
al trim:
Introducendo l’indice di stabilità statica:
(dove
per un velivolo stabile tradizionale),
possiamo scrivere:
È nec sviluppare una portanza d’incidenza maggiore rispetto a quanto nec per la pura sostentazione, in modo da
compensare la deportanza di controllo.
Discutere la loro var al variare di
variare di
e
e : Dato che
attraverso la
è conveniente caratterizzare di
. Consideriamo 2 cond di volo a diverse
e quindi per
mentre
per
otteniamo
e sostituendo nelle eq costit di port e res:
e
dato che
:
,
al trim in funz di :
e quindi
nell’espres della res trimmata:
(curva polare trimmata).
Per det la port trimmata, dalle eq:
e quindi
def:
e definendo il coeff:
termini di coeff adim:
Sist di rif orizz locale e gli angoli
e dalla
, otteniamo:
ossia la funz trimmata
pendenza della curva trimmata. Per un velivolo trad stat stab si ha
inferiore alla pendenza della curva di portanza ordinaria.
Ha origine nel pto mat
e pari
al
(velivolo tradizionale stabile).
Costruzione della curva polare trimmata: Dall’eq del centragg possiamo det
e sostituendo
e
, dove
rappresenta la
e quindi la pendenza della curva trimmata è
e , vel di volo mediante tali angoli, richiamando le nozioni
che rappr il veliv ed assi ortonorm
che in
e
:
t.c.:
Gli assi
e
sono allineati in direzione Nord ed Est, da cui la denominazione NED frame. Il rif orizz locale consente
di formalizzare le grandezze utili alla descrizione del moto del velivolo (es.
Quota di volo:
Angolo di rampa:
,
;
Velocità orizzontale e verticale:
,
Angolo di rotta :
,
La velocità di volo:
Soluz analitica di FC e SC per velivoli ad elica. Procedimento per via grafica, utilizzando i diagrammi di Pénaud:
Le eq di eq per la salita ad angoli di rampa moderati:
SC è def come la salita x la quale si ha
(vel di volo x cui è max l’esubero di spinta). FC è def come la
salita per la quale si ha
Motoelica semplificato
(vel di volo x cui è max l’esubero di potenza).
,
-
FC:
-
SC:
;
L’eq non consente una sol
analitica semplice ma è possibile ottenere una soluzione numerica attraverso un procedimento iterativo.
Si dimostri il probl di Froude, discutendo le limitazioni del modello propulsivo adottato rispetto alla realtà fisica.
Consideriamo la th del disco attuatore, per cui valgano le hp:
-
Condizioni stazionarie;
Flusso indisturbato a monte dell’elica assiale e uniforme;
Tubo di flusso corrispondente alla portata elaborata dall’elica;
Elica = disco di spessore infinitesimo (sup di discontinuità);
Corrente incomprimibile
Consideriamo
come generata dalla diff di press sulla supe del disco attuatore:
Dal principio di conserv della massa, e sapendo che
Applicando il th di Bernoulli tra le sezioni
e
(spinta dell’elica).
:
e le sez
.
e
, sapendo che
:
.
Sapendo che:
, e dall’eq di conserv della massa:
(Th di Froude). La vel sul disco dell’elica è la media tra la vel di captaz e quella
di eiez. L’elica induce un’accel del flusso che si ripartisce al
a monte della stessa e al
a valle (th di Froude).
Le stime ottenute con la th del disco attuatore risultano ottimistiche per quanto riguarda spinta e rendimenti, dato
che nel modello adottato non sono presenti dissipaz, né perdite cinetiche legate alla torsione della scia dell’elica.
Autonomia oraria per Jetto in condizioni di
Le eq di eq in LF ad
traiettoria:
ed
cost:
ed
.Def l’autonomia oraria come il tempo di percorrenza della
e sapendo che la portata di comb è:
.La condiz di
, quindi possiamo scrivere:
corrisponde alla max durata della crociera dato un certo quantitativo di comb,
oppure al min consumo di comb data una certa durata del volo (cercata x ottimizzare le fasi di attesa in volo).
Definendo il cons spec per un getto:
scivere:
:
(per un turbogetto sempl non dip da
e dalle eq di eq:
approx assunte,
, dove
.
non dipende né da
) possiamo
. Considerando una crociera a
cost (crociera-salita):
abbiamo
e da
cresce al diminuire di
né da
e all’aumentare di
e
.Qndi
, mentre per le hp e le
.
Criterio di stab stat long:
Lo studio della stab stat long è nec x caratterizz il comportamento istantaneo del velivolo in risposta a piccole
perturb del suo stato di eq. (si studia la tendenza del velivolo a contrastare o accentuare l’effetto di una perturb di
un suo stato di eq, limitatamente all’istante stesso del disturbo). La stab stat è presupposto fondamentale per
ottenere la stab dinamica. Consideriamo un velivolo in volo rett unif simm; il velivolo è centrato se:
(condiz di eq di trim). Supponendo che il velivolo sia sottoposto ad una perturb
e che il valore stesso di
incidenza di trim sia piccolo, possiamo assumere che il mom di becc subisca una variaz lineare, proporzionale a
Inoltre, assumendo condiz di comandi bloccati, otteniamo:
Date le convenzioni sui segni di e
, che risultano concordi (positivi nella direz di rotaz positiva sul piano
simm materiale del velivolo) si deduce che:
-
Se
Se
(a cabrare) la stab stat implica che
(a picchiare) la stab stat implica che
.
di
(a picchiare);
(a cabrare);
Qndi per avere stab stat è necessario che:
(condiz di stab stat long a comandi bloccati).
discutendo il significato del M.S.: Dall’espressione:
, avendo appena ricavato
sapendo che
(M.S. a comandi bloccati). La stab stat è assicurata se è davanti a .
,e
Il criterio di stab long richiede semplicemente che il M.S. sia positivo; maggiore è il margine statico, maggiore sarò
l’effetto di richiamo esercitato dal momento di beccheggio in risposta ad una perturbazione.
Dim effetto stab dell’imp orizz: L’imp orizz fornisce l’essenziale contributo stabilizzante. Infatti, assumendo che:
, dalla regola del trasp otteniamo il contributo dell’impennaggio al mom di
beccheggio baricentrale dell’intero velivolo come:
e derivando rispetto ad
(descrive l’effetto stab della sup). Essendo
:
, qsto contributo è stab (ossia
negativo) se:
(
si trova dietro a ). L’effetto stab sarà dunque maggiore quanto maggiori saranno i
valori del braccio e/o della pendenza della curva di portanza dello stabilizzatore
.
Autonomia chilometrica per Jetto in condizioni di
Le eq di eq in LF ad
ed
cost:
ed
traiettoria:
.Def l’autonomia chilometrica come lo spazio percorso sulla
e sapendo che la portata di comb è:
. La condiz di
, possiamo scrivere:
corrisponde alla max distanza percorsa in crociera dato un certo quantitativo di
comb, oppure al min consumo di comb data una certa distanza da coprire (Cercata per ottimizzare il trasf tra due
aerobasi). Definendo il cons spec per un getto:
possiamo scivere:
crociera a
e
:
(per un turbogetto sempl non dip da
e dalle eq di eq:
e da
)
. Considerando una
cost (croc-orizz decell):
,
.
cresce al diminuire di
dove
e all’aumentare di
.Qndi
abbiamo
.
Soluz analitica di FC e SC per velivoli a Jetto. Procedimento per via grafica, utilizzando i diagrammi di Pénaud:
Le eq di eq per la salita ad angoli di rampa moderati:
SC è def come la salita x la quale si ha
salita per la quale si ha
Consideriamo un Turbogetto semplificato:
-
SC:
(vel di volo x cui è max l’esubero di spinta). FC è def come la
(vel di volo x cui è max l’esubero di potenza).
-
FC:
dove
cresce al crescere di
. Utilizzando l’hp di polare parabolica,
, mentre
cresce al crescere di
otteniamo:
e al diminuire di
.
Si mostri, con es dall’analisi delle prestaz in crociera, come J risulti adatto al volo a vel più elevate di quelle di P.
Dall’analisi delle prestazioni in crociera sappiamo che:
-
per un turbogetto semplificato:
-
per motoelica semplificato:
Se analizziamo 2 tecniche di volo, quali crociera orizz-decel
-
per un turbogetto si ha:
-
per un motoelica si ha, invece:
Un turbogetto risulta conveniente a
mentre, un motoelica risulta conveniente a
e crociera-salita
, otteniamo:
, dato che gli ottimi prestazionali si trovano in quest’intervallo;
, dato che gli ottimi prestazionali si trovano in quell’intervallo.
Si mostri, con es dall’analisi delle prestaz in salita, come J risulti adatto al volo a vel più elevate di quelle di P.
Dall’analisi delle prestazioni in salita otteniamo:
Per un turbogetto semplificato:
-
SC:
-
FC:
essendo
, otteniamo che
L’uso di un velivolo a getto risulta conveniente a
, dato che gli ottimi prestaz si trovano in questo interv.
Per un motoelica semplificato:
-
FC:
-
SC:
, l’equazione non consente una soluzione analitica semplice ma è
possibile ottenere una soluzione numerica attraverso un procedimento iterativo;
essendo
, otteniamo che
L’uso di un velivolo a elica risulta conveniente a
intervallo.
Riassumendo:
, dato che gli ottimi prestazionali si trovano in questo
J
P
Si mostrino i termini che concorrono al momento di beccheggio del velivolo completo di architettura tradizionale :
Consideriamo un velivolo trad con imp posteriori. Il suo mom di becc sarà dato da:
, dove
.Quindi il coeff di mom di becc dell’intero velivolo sarà:
dove
,
.Resta da caratterizz la dip del coeff di mom di becc delle 2 sup dagli angoli di incidenza locali e di
deflessione dell’equilibratore:
-
Per l’ala abbiamo:
, dove
, (dove
è la pendenza
del coeff di portanza del velivolo parziale,
la pendenza del coeff di port del velivolo parziale rispetto alla
deflessione dell’equilibr e
l’incidenza del velivolo parziale);
-
Per l’impennaggio orizzontale:
, dove
, (dove
è la
pendenza del coeff di portanza dell’imp,
la pendenza del coeff di port dell’imp orizz rispetto alla
deflessione dell’equilibr e
l’incidenza dell’imp orizz).
Si def T, P e
nel caso di prop a motoelica e a razzo:
Motoelica: La portata elaborata è costituita dalla portata d’aria accelerata dall’elica più la portata di comb bruciato
che non contribuisce alla spinta. Qndi otteniamo:
dove
solo se riesco ad accelerare la massa d’aria elaborata ed è proporzionale al salto di velocità impresso al flusso.
Le potenze risultano:
Il rendimento prop:
dove
quando
(elica non funzionante) e cresce al diminuire di
.
Abbiamo elevati
quando il salto di vel imposto al flusso dall’elica è modesto. Per ottenere valori di spinta
accettabili si dovranno elaborare elevate portate d’aria. Le velocità di volo operative corrispondono a condizioni di
basso-medio regime subsonico, per motivi di tipo aerodinamico e strutturale.
Endoreattore: Tutto il flusso è prodotto dalla combustione del propellente contenuto all’interno del velivolo.
Otteniamo quindi:
Le potenze risultano:
(non dip dalla velocità di volo)
mentre:
Si possono ottenere valori accettabili di
anche per
, dal momento che T non dip dalla vel di volo. Inoltre
per
si ha
, in quanto tutta l’en scambiata viene convertita in spinta, essendo i gas di scarico fermi
rispetto all’ambiente. Un funzionamento ideale dal punto di vista energetico comporta condizioni operative in cui la
vel di volo è prossima alla vel di eiezione. Per questo, i prop a razzo sono utilizzati di norma per elevatissime velocità
operative. Inoltre, hanno il vantaggio che le loro caratt non variano con la quota.
Autonomia chilometrica per un Motoelica in condizioni di
Le eq di eq in LF ad
traiettoria:
ed
ed
cost:
.Def l’autonomia chilometrica come lo spazio percorso sulla
e sapendo che la portata di comb è:
. La condiz di
, possiamo scrivere:
corrisponde alla max distanza percorsa in crociera dato un certo quantitativo di
comb, oppure al min consumo di comb data una certa distanza da coprire (Cercata per ottimizzare il trasf tra due
aerobasi). Definendo il cons spec per un motoelica:
possiamo scivere:
:
(per un motoelica sempl non dip da
e da
)
e dalle eq di eq:
Considerando una crociera a
e
dove
.Qndi
.
cost (croc-orizz decell):
.
,
cresce all’aument di
e di e al diminuire di
.
Formule di Rénard per T e C dell’elica e grafici per i relativi coeffadimensionali, discutendo i diversi regimi:
Supponendo condizioni di volo rettilineo, uniforme e simmetrico, è possibile dedurre che T e C sono funzione di:
(dove
è il num di giri,
la vel di volo,
la dens di rif,
la visc di rif,
il
diam del disco dell’elica,
il numero di pale,
il calettamento nominale e
tiene conto della forma e del
grado di rifinitura superficiale). Per fare l’anal dim delle azioni prop utilizziamo il th di Buckingham (ad es per ):
, dove
sono grandezza adim indip tra loro e possono
essere escluse dal seguente procedimento. Qndi abbiamo:
variabili fisiche e
grandezze fondamentali che ci consentono di scrivere
var adim. Assumiamo che vi sia una relaz:
, ovvero:
. Per det le 4 var adimensionali
, scegliamo le 3 variabili fisiche
quali indipendenti e quindi scriviamo:
e
quindi
le
Ricaviamo:
var
adim
risultano:
(formule di Rénard)
Quindi 2 eliche identiche nelle forme ma non nella dim, rotanti a n° di giri diverso ed immerse in
flussi diversi per
ma tali da fornire uguali valori di
di volo, sviluppano
identici.
I regimi di funzionamento dell’elica risultano:
Regimi
Elica a pto fisso
Elica traente
Elica a T nulla
Elica frenante
Elica autorotante
Si ha T max e si verifica qndo è fermo al suolo con l’elica in moto
T utilizzata sia per vincere la res.aerod. che per acc. Il flusso che attraversa
il disco dell’elica (condizioni normali d’impiego)
C spesa per vincere la res.aerod. delle pale
C spesa per frenare il velivolo (discesa)
Pot.nec. x vinc la res.aero delle pale fornita dal flusso che l’attr (discesa)
Elica a mulinello
Elica bloccata
L’elica fornisce en. al motore (pericolosa x il propulsore)
(es.avaria) La C che tende a far ruotare l’elica assume valori molto
elevati.Nelle eliche a passo var. si mettono le pale “a bandiera”
Si discutano le regolazioni dell’altimetro barometrico, spiegandone il significato e l’impiego in funzione delle fasi
di volo.
Uno scostamento dell’atmosfera del giorno dall’ISA può comportare una differenza rilevante tra quota di pressione a
quota vera. Questo può rappresentare un probl nelle fasi di avvicinamento o allontanamento da terra e per il volo a
bassa quota. Per evitare questo problema è possibile regolare l’altimetro su diversi valori di pressione di riferimento:
-
-
-
QNE
(pressione ISA@
); utilizzata nelle fasi di volo non terminali per garantire un’adeguata
separazione verticale tra i velivoli. Le spinte indicate dalla regolazione QNE vengono dette “flight level” e sono
misurate in centinaia di piedi. La separazione imposta dalle normative è pari a
o eventuali multipli;
QNH
(press al m.s.l. nell’atmosfera del giorno); utilizzata nelle fasi di volo terminali per garantire
un’adeguata separazione verticale dagli ostacoli al suolo. Quando il velivolo si trova sull’aerobase, l’altimetro
segna la quota esatta dell’aerobase stesso poiché
viene calcolata a partire dal valore di pressione
sull’aerobase. Le quote indicate dalla regolazione QNH vengono dette “altitudes” e misurate in piedi;
QFE
(valore locale di press sull’aerobase); utilizzata nelle fasi di volo terminali, sebbene stia
cadendo in disuso. Quando il velivolo si trova all’aerobase, l’altimetro segna esattamente 0. Le quote indicate
dalla regolazione QFE vengono dette “heights” e misurate in piedi.










