Algebra
SINTESI
Unità 2
Le operazioni fondamentali con i numeri relativi
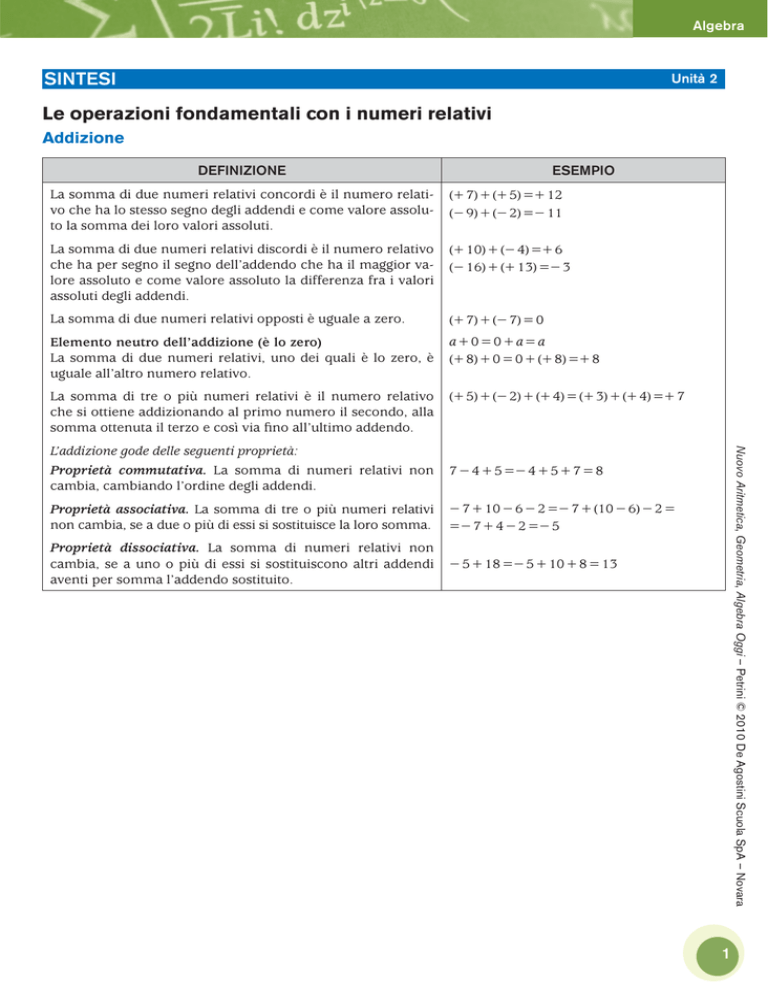
Addizione
DEFINIZIONE
ESEMPIO
La somma di due numeri relativi concordi è il numero relativo che ha lo stesso segno degli addendi e come valore assoluto la somma dei loro valori assoluti.
(+ 7) + (+ 5) =+ 12
(- 9) + (- 2) =- 11
La somma di due numeri relativi discordi è il numero relativo
che ha per segno il segno dell’addendo che ha il maggior valore assoluto e come valore assoluto la differenza fra i valori
assoluti degli addendi.
(+ 10) + (- 4) =+ 6
(- 16) + (+ 13) =- 3
La somma di due numeri relativi opposti è uguale a zero.
(+ 7) + (- 7) = 0
Elemento neutro dell’addizione (è lo zero)
La somma di due numeri relativi, uno dei quali è lo zero, è
uguale all’altro numero relativo.
a+0=0+a=a
(+ 8) + 0 = 0 + (+ 8) =+ 8
La somma di tre o più numeri relativi è il numero relativo
che si ottiene addizionando al primo numero il secondo, alla
somma ottenuta il terzo e così via fino all’ultimo addendo.
(+ 5) + (- 2) + (+ 4) = (+ 3) + (+ 4) =+ 7
7 - 4 + 5 =- 4 + 5 + 7 = 8
Proprietà associativa. La somma di tre o più numeri relativi
non cambia, se a due o più di essi si sostituisce la loro somma.
- 7 + 10 - 6 - 2 =- 7 + (10 - 6) - 2 =
=- 7 + 4 - 2 =- 5
Proprietà dissociativa. La somma di numeri relativi non
cambia, se a uno o più di essi si sostituiscono altri addendi
aventi per somma l’addendo sostituito.
- 5 + 18 =- 5 + 10 + 8 = 13
Nuovo Aritmetica, Geometria, Algebra Oggi – Petrini © 2010 De Agostini Scuola SpA – Novara
L’addizione gode delle seguenti proprietà:
Proprietà commutativa. La somma di numeri relativi non
cambia, cambiando l’ordine degli addendi.
1
Algebra
Sottrazione
DEFINIZIONE
ESEMPIO
Si dice differenza fra due numeri relativi quel terzo numero
relativo che, addizionato al secondo, dà per somma il primo.
(+ 7) - (+ 2) =+ 5
perché
(+ 5) + (+ 2) =+ 7
La differenza fra due numeri relativi si ottiene addizionando
al primo (minuendo) l’opposto del secondo (sottraendo).
(+ 9) - (+ 5) = (+ 9) + (- 5) = 4
La differenza fra due numeri relativi uguali è uguale a zero.
(- 5) - (- 5) = 0
Si dice addizione algebrica una successione di addizioni e di
sottrazioni fra numeri relativi. Il risultato di un’addizione algebrica si dice somma algebrica.
(+ 7) + (- 5) + (- 3) + (+ 2) = 1
Nuovo Aritmetica, Geometria, Algebra Oggi – Petrini © 2010 De Agostini Scuola SpA – Novara
2
Algebra
Moltiplicazione
DEFINIZIONE
ESEMPIO
Il prodotto di due numeri relativi (entrambi diversi da zero) è
il numero relativo che ha per valore assoluto il prodotto dei
valori assoluti e per segno:
a. il segno + se i fattori sono concordi;
b. il segno - se i fattori sono discordi.
(+ 5) $ (+ 3) =+ 15
(- 5) $ (- 3) =+ 15
(+ 5) $ (- 3) =- 15
(- 5) $ (+ 3) =- 15
Il prodotto di più numeri relativi è il numero relativo che ha
per valore assoluto il prodotto dei valori assoluti di tutti i fattori ed è positivo se i fattori negativi sono in numero pari o
negativo se i fattori negativi sono in numero dispari.
(+ 5) $ (- 3) $ (- 2) =+ 30
(+ 4) $ (+ 2) $ (- 5) =- 40
Il prodotto di numeri relativi è uguale a zero, se almeno uno
dei fattori è uguale a zero.
(+ 5) $ 0 = 0
0 $ (- 7) = 0
(+ 3) $ (+ 2) $ (- 7) $ 0 = 0
Elemento neutro della moltiplicazione (è l’unità positiva = + 1)
Moltiplicando un numero relativo per +1 otteniamo il numero stesso.
In generale: a $ (+ 1) = (+ 1) $ a = a
(+ 5) $ (- 3) = (- 3) $ (+ 5) =- 15
Proprietà associativa. Il prodotto di tre o più numeri relativi
non cambia se a due o più di essi si sostituisce il loro prodotto.
(+ 5) $ (+ 2) $ (- 3) = (+ 10) $ (- 3) =- 30
Proprietà dissociativa. Il prodotto di numeri relativi non
cambia, se uno dei fattori viene sostituito da due o più fattori,
il cui prodotto sia uguale al fattore sostituito.
(+ 10) $ (+ 3) = (+ 2) $ (+ 5) $ (+ 3) = 30
Proprietà distributiva rispetto all’addizione algebrica. Per
moltiplicare una somma algebrica indicata di numeri relativi
per un numero relativo, si può moltiplicare ciascun addendo
per quel numero e addizionare poi i prodotti così ottenuti.
(a + b + c) $ h = a $ h + b $ h + c $ h
(- 3 + 5 - 8) $ (+ 2) = (- 3) $ (+ 2) + (+ 5) $
$ (+ 2) + (- 8) $ (+ 2) =- 6 + 10 - 16 =- 12
Proprietà distributiva rispetto a due somme algebriche indicate. Per moltiplicare una somma algebrica indicata per
un’altra, si può moltiplicare ciascun addendo di una somma
per ciascun addendo dell’altra e addizionare poi i prodotti ottenuti.
(a + b + c) $ (h + k) = a $ h + b $ h + c $ h +
+a$k+b$k+c$k
(- 3 + 4 - 6) $ (- 5 + 2) =+ 15 - 20 + 30 - 6 +
+ 8 - 12 = 15
Nuovo Aritmetica, Geometria, Algebra Oggi – Petrini © 2010 De Agostini Scuola SpA – Novara
La moltiplicazione gode delle seguenti proprietà:
Proprietà commutativa. Il prodotto di numeri relativi non
cambia cambiando l’ordine dei fattori.
(+ 5) $ (+ 1) =+ 5
(+ 1) $ (+ 5) =+ 5
3
Algebra
Divisione
DEFINIZIONE
ESEMPIO
Due numeri relativi si dicono inversi o reciproci fra loro se il - 3 e - 4 sono inversi
4
3
loro prodotto è uguale a +1.
3 l b 4 l
perché b$ =+1
4
3
Si dice quoziente fra due numeri relativi, di cui il secondo sia
diverso da zero, il numero relativo che, moltiplicato per il secondo, dà per prodotto il primo.
(+ 15) : (- 3) =- 5
perché
(- 5) $ (- 3) =+ 15
Il quoziente fra due numeri relativi è il numero relativo che
ha per valore assoluto il quoziente fra i valori assoluti dei numeri dati, e per segno il segno + se il dividendo e il divisore
sono concordi o il segno - se essi sono discordi.
(+ 15) : (+ 3) =+ 5
(- 15) : (- 3) =+ 5
(+ 15) : (- 3) =- 5
(- 15) : (+ 3) =- 5
Il quoziente fra due numeri relativi, di cui il secondo non nullo, si può ottenere moltiplicando il primo per il reciproco del
secondo.
(- 4) : b-
Proprietà distributiva rispetto all’addizione algebrica. Per
dividere una somma algebrica indicata per un numero relativo (diverso da zero) si può dividere ciascun termine della
somma algebrica indicata per quel numero relativo e addizionare i quozienti parziali ottenuti.
- 40 : 8 =- 5
(- 40 $ 2) : (8 $ 2) =- 80 : 16 =- 5
(- 40 : 2) : (8 : 2) =- 20 : 4 =- 5
Nuovo Aritmetica, Geometria, Algebra Oggi – Petrini © 2010 De Agostini Scuola SpA – Novara
La divisione gode delle seguenti proprietà:
Proprietà invariantiva. Se si moltiplicano (o si dividono) il
dividendo e il divisore di una divisione per uno stesso numero relativo diverso da zero, il quoziente rimane invariato.
1 l
= (- 4) $ (- 2) =+8
2
(- 9 - 6 + 18) : (- 3) =
=- 9 : (- 3) - 6 : (- 3) + 18 : (- 3) =
= 3 + 2 - 6 =- 1
4
Algebra
Espressioni numeriche
DEFINIZIONE
ESEMPIO
Espressione algebrica numerica, o semplicemente
espressione numerica, è un insieme di numeri relativi
legati fra loro con i segni delle operazioni.
(+ 5) $ (- 2) + (- 24) : (- 6) + (- 7)
Un’espressione numerica può non avere o avere parentesi.
: b 2 - 1 l $ b- 3 l + b- 2 l $ b1 - 4 l D : b- 11 l
3
4
3
5
60
In un’espressione numerica senza parentesi le operazioni si eseguono nel seguente ordine:
1. moltiplicazioni e divisioni secondo l’ordine con cui
si presentano;
2. addizioni e sottrazioni secondo l’ordine con cui si
presentano.
(- 7) $ (- 3) + (- 39) : (+ 13) + (- 20) =
= 21 - 3 - 20 =- 2
In un’espressione numerica con parentesi si calcola prima il valore delle espressioni contenute nelle parentesi più interne rispettando le regole di precedenza delle operazioni.
Le parentesi si eliminano dopo aver eseguito tutte le operazioni in esse contenute.
In tal modo otteniamo un’espressione numerica senza parentesi.
-5 + : 2 - b 2 -
1
3 l: 1 D:b
1
1 l
+
-3 +
=
2
4
8
2
3
8 - 2 + 3 : 1 D : -18 + 3 - 2
=
4
8
6
=-5 + : 2 -
9 : 1 D : b 17 l
=
4 8
6
=-5 + : 2 -
9
17 l
$ 8 D : b=
4
6
=-5 + [2 - 18] : b-
17 l
=
6
=-5 + (- 16) $ b-
6 l
=
17
=-5 +
Nuovo Aritmetica, Geometria, Algebra Oggi – Petrini © 2010 De Agostini Scuola SpA – Novara
=-5 + : 2 -
96
-85 + 96
11
=
=
17
17
17
5