Politecnico di Torino - Facoltà di Ingegneria
Corso di laurea in Ingegneria Civile
Rivisto:1/03/2011
Punti: 9
Laboratorio di sintesi finale – F: Biasioli
Argomenti:
1.3
Caratteristiche di sollecitazione, simmetrie e antisimmetrie, sviluppi in seerie
Caratteristiche di sollecitazione
Suddividendo un corpo in equilibrio in due parti attraverso una sezione normale all’asse nascono sulle due
facce della sezione delle reazioni interne che, essendo il corpo, in equilibrio, devono avere intensità tale da
mantenere ciascuna delle due parti isolate in equilbrio.
Si fissa e un sistema di riferimento cartesiano ortonormale O(x, y, z) con origine nel baricentro della
sezione, assi x e y che giacciono nel piano della sezione traversale della trave, asse y convenzionalmente
orientato verso il bassoi e asse z tangente all’asse baricentrico della trave.
Si definiscono caratteristiche di sollecitazione le componenti in tale riferimento della forza R e del
momento risultante M che si ottengono trasportando tutte le forze che precedono o seguono la sezione nel
baricentro della generica sezione.
Con riferimento alla terna (x y z), i vettori R e M possono essere proiettati sulle direzioni x,y e z : si
ottengono tre componenti della forza R e tre componenti del momento M, dette rispettivamente Tx, Ty
(forze di taglio) Nz (forza assiale o sforzo normale) e Mx, My (momenti flettenti ) eMz (momento torcente).
Se tutte le forze sono contenuta nel piano (zy) del sistema di riferimento le caratteristiche della
sollecitazione si riducono a tre (vedi figura):
(1) la forza assiale Nz ;
(2) la forza di taglio Ty;
(3) il momento flettente Mx.
Nel caso piano per identificare il verso delle caratteristiche di sollecitazione e tracciare i loro diagrammi
(diagrammi di M,N,T) è necessario definire dei riferimenti e delle notazioni (convenzioni di segno).
Si assumono convenzionalmente positive la forza assiale di
trazione, la forza di taglio che tende a far ruotare in senso
orario il tronco di trave su cui agisce e il momento flettente
che tende le fibre inferiori (poste dalla parte dell’asse y
positivo) e comprime le superiori. La faccia che “guarda”
verso le coordinate z crescenti è detta “positiva”; quella
opposta, che “guarda” verso z decrescenti, è detta
“negativa”. La figura visualizza le convenzioni:
Le funzioni momento Mx, taglio Ty, forza assiale Nz e un
eventuale carico distribuito sono legate tra loro da equazioni
differenziali. Si consideri un tronco di trave di lunghezza
infinitesima dz sottoposto ad un carico distribuito
tangenziale p(z), a un carico distribuito normale q(z) e alle
sollecitazioni
Mx(z), Ty(z), Nz(z), e Mx(z) + dMx, Ty(z) + dTy, Nz(z) + dNz,
sulle sezioni di estremità.
Imponendo l’equilibrio alla traslazione orizzontale :
La derivata dello sforzo normale rispetto alla coordinata assiale è uguale all’opposto del carico distribuito
assiale.
Imponendo l’equilibrio alla traslazione verticale:
La derivata del taglio rispetto alla coordinata assiale è uguale all’opposto del carico distribuito ortogonale
all’asse.
Imponendo l’equilibrio alla rotazione rispetto al punto di mezzeria del concio di trave e trascurando gli
infinitesimi di ordine superiore si ha :
Per tracciare le funzioni M,N e T. è utile applicare le regole relative allo studio delle funzioni
Esempio 1: trave di lunghezza l appoggiata ad entrambe le estremità con carico distribuito uniforme (q).
Le reazioni vincolari verticali sono due forze equiverse pari a ql/2.
La reazione vincolare orizzontale nel punto B è nulla in quanto non
sono presenti forze orizzontali. La forza assiale Nz è ovunque nulla
poiché non vi sono forze applicate lungo l’asse z.
Esplicitando la funzione momento si ha la funzione di II° grado:
2
2
Il diagramma del momento si annulla all’ascissa z=0 e z=l.
Derivando, si trova la funzione di taglio:
T(0) =
T(l) = Per z < l/2 la derivate della funzione taglio è positive dunque la
funzione è crescente. Il diagramma del taglio è lineare e si annulla
in mezzeria, dove il momento è massimo e vale:
8
Esempio 2: trave di lunghezza l soggetta a due forze concentrate poste ad ¼ l e ¾ l.
Le reazioni vincolari verticali sono due forze equiverse pari a
F, la reazione vincolare orizzontale nel punto B è nulla.
La forza assiale Nz è ovunque nulla poiché non vi sono forze
applicate lungo l’asse z.
Funzioni momento e taglio:
Per 0 z l/4
M(z) = Fz
T(z) =
F
= costante
Per l/4 z < 3l/4
M(z) = Fl/4
T(z) = 0
Per l/4 < z l
M(z) = Fl/4 Fz
T(z) = Fz
Il diagramma di momento è lineare nelle zone comprese tra
il vincolo e la forza applicata, costante nella zone in cui il
taglio è nullo compresa tra le due forze applicate. Il
momento massimo vale: M = Fl/4
Esempio 3: mensola di lunghezza l soggetta ad una forza F ortogonale all’asse applicata nell’estremità B.
La reazione vincolare verticale è una forza di modulo F applicata
nell’incastro e un momento antiorario di modulo Fl.
La forza assiale Nz è ovunque nulla poiché non vi sono forze applicate
lungo l’asse z.
Il diagramma del taglio è costante lungo tutta la mensola e vale F . Il
diagramma del momento è lineare e si annulla nell’estremità B. Il
momento massimo si ha nell’ incastro e ha modulo pari a M = Fl.
Si analizzi, per esempio, una mensola caricata in estremo, come in
figura.
Le sollecitazioni agenti sulla generica sezione trasversale z possono
essere calcolati indifferentemente sulla base delle forze e momenti
agenti prima o dopo la sezione: in entrambi i casi sono da considerarsi
positive le forze e le coppie concordi con le convenzioni proprie della faccia, “positiva” o “negativa”.
Analizzando le caratteristiche della sollecitazione partendo dall’estremo libero della trave (quindi con la
convenzione delle facce positive),:
• La forza di taglio in punta è pari in modulo alla forza P, il verso secondo convenzione delle facce
positive è positivo (suggerisce rotazione oraria del concio a monte); il taglio permane costante sulla
trave, fino a verificare l’equilibrio nella sezione d’incastro.
• il momento in punta è nullo (in quanto non vi sono coppie applicate all’estremo libero); per opera
della forza P, allontanandosi dalla sezione di estremo libero, si genera un momento sollecitante che
varia in modo lineare (taglio costante), aumenta con l’aumentare del braccio ed ha segno negativo,
in quanto tende le fibre superiori; nella sezione d’incastro si verifica l’equilibrio per opera della
coppia d’incastro Pl.
Analizzando le caratteristiche della sollecitazione partendo dalla sezione d’incastro (quindi con la
convenzione delle facce negative), emerge che:
• il taglio all’incastro è pari in modulo alla forza P, il verso secondo convenzione delle facce positive è
positivo (suggerisce rotazione oraria del concio a valle); il taglio permane costante sulla trave, fino a
verificare l’equilibrio nell’estremo.
• il momento all’incastro è pari a Pl con segno negativo (tende le fibre superiori); proseguendo verso
destra, il momento sollecitante si attenua linearmente perché Pl è progressivamente compensato
dall’incremento di momento positivo dovuto alla forza verticale d’incastro (che tende le fibre
inferiori), il che porta a verificare l’equilibrio nell’estremo libero.
I due approcci (analisi “a valle” o “a monte” della sezione), basati sulle convenzioni di segno sopra esposte,
conducono ovviamente allo stesso risultato.
Simmetrie e antisimmetrie
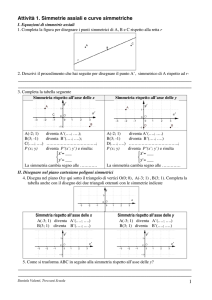
Si definisce simmetrica una struttura dotata di un asse di simmetria per geometria . Perché una struttura
possa essere definta simmetrica è necessario che siano simmetrici anche i vincoli “efficaci”, quelli cioè che
offrono il contributo statico di reazione vincolare. Ad esempio sono vincoli efficaci simmetrici:
- due carrelli;
- due cerniere;
- un carrello e una cerniera in assenza reazione orizzontale;
Il concetto di simmetria può essere pensato come un ribaltamento speculare di una delle due parti divise
dall’asse di simmetria sul’altra
Una struttura simmetrica può essere caricata simmetricamente o antisimmetricamente. Il concetto di
simmetria di carico può essere pensato come un ribaltamento speculare di una delle due parti divise
dall’asse di simmetria sul’altra: per l’antisimmetria occorre moltiplicare per ( -1) tutti i carichi così ribaltati,
cambiando il verso delle grandezze vettoriali pur conservandone la direzione.
In una struttura simmetrica caricata simmetricamente sono simmetriche le reazioni vincolari, gli
spostamenti e le rotazioni paralleli all’asse di simmetria,
simmetria le sollecitazioni di forza assiale e momento. La
sollecitazione di taglio e le rotazione
otazione e spostamento perpendicolari all’asse di simmetria sono viceversa
antisimmetrici. Avremo dunque:
• Diagrammi di forza assiale e di momento flettente simmetrici
• Diagramma di taglio antisimmetrico
• Rotazione e spostamento paralleli
para
all’asse di simmetria simmetrici
• Rotazione e spostamento perpendicolari all’asse di simmetria
s
antisimmetrici
immetrici
Una struttura simmetrica caricata simmetricamente n volte iperstatica perde un grado di iperstaticità
perchè si può sostituire metà struttura con un vincolo che rispetti le condizioni di deformazione iniziali.
iniziali
Esempi di strutture simmetriche caricata simmetricamente:
In una struttura simmetrica caricata antisimmetricamente le situazioni precedenti si invertono: sono
antisimmetriche le reazioni vincolari, gli spostamenti e le rotazioni. Vremo
remo dunque
• Diagrammi di forza assiale e di momento flettente antisimmetrici
• Diagramma di taglio simmetrico
• Rotazione e spostamento paralleli
para
all’asse di simmetria antisimmetrici
• Rotazione e spostamento perpendicolari all’asse di simmetria
s
simmetrici
Se la struttura caricata simmetricamente si riusciva a perdere un grado di iperstaticità, in questo caso se ne
riesce a perdere uno in più se si sostituisce metà struttura con un vincolo che rispecchi gli spostamenti, le
rotazioni e i vincoli preesistenti
Esempio di strutture simmetrica caricata anti simmetricamente:
Sull’asse di simmetria le caratteristiche antisimmetriche devono essere nulle. Infatti, immaginando il concio
di trave infinitesimo disposto sull’asse di simmetria, per esso devono valere contemporaneamente
contemporaneam
le
condizioni di equilibrio e di antisimmetria; condizioni mutuamente esclusive a meno della soluzione nulla.
In presenza i forze concentrate, quanto appena detto potrebbe
potrebbe non sembrare evidente ad una prima
osservazione della struttura. La Figura (a) mostra un caso di struttura simmetrica caricata simmetricamente
e ne riporta il diagramma di taglio. Per quanto detto in precedenza esso si deve annullare in corrispondenza
dell’asse di simmetria della trave, anche se, la discontinuità che il diagramma manifesta in mezzeria tende a
rendere meno visibile questo aspetto.
In realtà ogni forza è distribuita su di una superficie
superfic o lunghezza finita, come si vede in Figura (b), e il
concetto di “forza puntuale” è, come ili punto in geometria, un’astrazione teorica che si realizza al tendere a
zero della larghezza di carico. Nel caso di forze applicate in un punto, pertanto, le caratteristiche
antisimmetriche ( in questo caso il taglio) sono nulle sull’asse di simmetria.
Esiste anche un altro tipo di simmetria, la simmetria
sim
polare. Un
n sistema di travi risulta simmetrico rispetto
ad un polo O (vedere figure1 e 2), allorché una delle due metà in cui la struttura è suddivisa dal polo O vada
a sovrapporsi all’altra, se fatta ruotare di 180° attorno al polo stesso.
Le stutturee polar simmetriche possono essere a loro volta caricate simmetricamente (a sinistra) o anti
simmetricamente (a destra).
In una struttura polarsimmetrica
metrica caricata simmetricamente le sollecitazioni
ioni che agiscono su di una metà
fatte ruotare di 180° vanno a sovrapporsi a quelle che agiscono sulla metà rimanente.
Nel polo il momento flettente si annulla così come lo spostamento per ragioni polarsimmetriche, di
equilibrio e di congruenza. Tali condizioni
condizioni sono realizzate da una cerniera, quindi tale struttura se n volte
iperstatica studiata dimezzata risulta essere (n-1) volte iperstatica .
In una struttura pola-simmetrica
simmetrica caricata antisimmetricamente
anti
le sollecitazioni che agiscono su una delle
del
due metà sono le opposte alle simmetriche rispetto alle sollecitazioni che agiscono sulla restante metà.
Nel polo si annullano sia lo sforzo normale, sia il taglio che la rotazione elastica per farsi che si verifichino
l’equilibrio, la congruenza e le caratteristiche
aratteristiche antipolarsimmetriche. Tali condizioni sono realizzate da un
doppio doppiopendolo. In questo caso se la struttura fosse stata n volte iperstatica, si studia, con
l’introduzione di un doppio doppiopendolo, con un grado di iperstaticità (n-2)
(n minore.
inore.
Sviluppi in serie della funzione momento
Si consideri una generica funzione y(z). Vale, sotto precise ipotesi dell’analisi (funzione f definita in un
intervallo aperto (a − r, a + r) a valori reali e derivabile fino all’ordine n), lo “ sviluppo in serie di Mac Laurin”
nell’intorno dell’origine z = 0. Troncando lo sviluppo al quarto ordine si ottiene:
"
0 0 0 0 ! 0
2
6
24
Se alla funzione y si attribuisce il significato fisico di linea elastica di una struttura costituta da un sistema di
travi (modello di Eulero-Bernoulli), considerando positivi gli abbassamenti e le rotazioni antiorarie e tenuto
conto che:
$
$ $ $
$
$ valgono le relazioni:
Sostituendo si ottiene:
%&
%
'
%( &
% (
)
%* &
% *
+
)
%, &
% ,
- - - "
./ 2 ./ 6 ./ 24
- - '- ./
./ 2 ./ 6
- - 00 ./ ./
./ 2
./ ./
./ - - 2
./ - )
- '- Note le espressioni delle derivate seconda e terza di y, è possibile scrivere le funzioni M e T in qualsiasi
tratto della struttura se sono noti a) i valori che esse assumono nel punto scelto come origine e b) i carichi
agenti nel tratto successivo.
Tutte le funzioni hanno espressione unica in un dato tratto solo se nella funzione in esame o in quella di
una qualsiasi delle sue derivate successive non siano presenti delle discontinuità.
Ad esempio in una trave isostatica un carico in mezzeria introduce nel punto di applicazione una
discontinuità nell’espressione della funzione
taglio: di
conseguenza si avranno due espressioni, diverse tra loro, delle
funzioni linea elastica, pendenza e momento, una prima del
punto di applicazione della forza, una dopo il punto di
applicazione della forza. Ovviamente si può mettere una origine
locale nel punto di applicazione della forza, assumendo come
y(0) y’(0) M(0) e T(0) i valori di y, y’ M e T che si hanno un
infinitesimo prima del punto di applicazione.
3
3
456 0 7 7 ,
1 2
2
2
3
3
2 4
456 7 7 ,
2
2
2
2
1 2 L’origine scelta per lo sviluppo in serie può essere un qualsiasi punto 0 della trave, purché in esso siano
note le caratteristiche della sollecitazione M(0), N(0) e T(0). Si conclude che il valore degli effetti dei carichi
non è influenzato da ciò che avviene “a monte” della sezione presa come origine, purché in essa si conosca
le risultanti delle forze e dei momenti di trasporto che i due conci di trave separati dalla sezione si
scambiano reciprocamente.