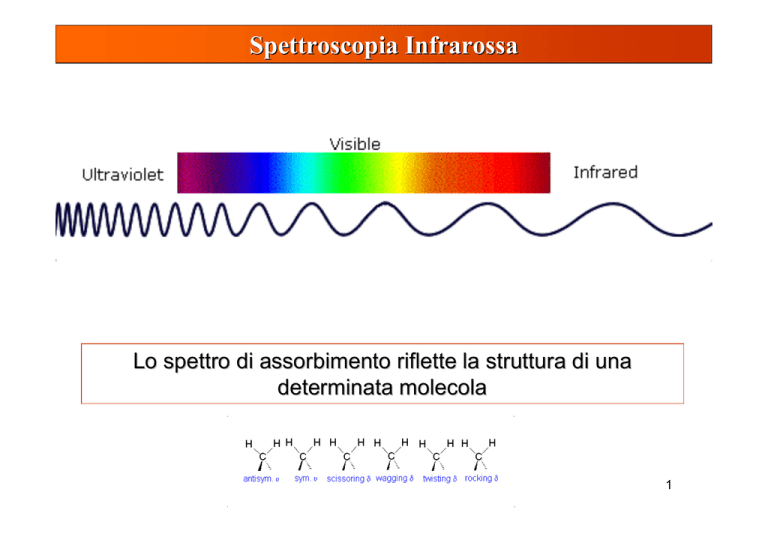
Spettroscopia Infrarossa
Lo spettro di assorbimento riflette la struttura di una
determinata molecola
1
APPLICAZIONI
La spettroscopia IR (vibrazionale) dà informazioni sulle forze
di legame e sulla geometria molecolare. Dal punto di vista
dell’analisi chimica è una tecnica utile per il riconoscimento
dei gruppi funzionali nelle molecole
2
LA RADIAZIONE INFRAROSSA
3
La regione dell’infrarosso
La spettroscopia IR si basa sull'assorbimento da parte di composti,
di radiazioni con lunghezze d'onda comprese tra 0,78 µm e
100 µm. 24
Questa gamma spettrale viene suddivisa in tre regioni principali:
-IR vicino
-IR medio
-IR lontano
0,78 a 2,5 µm
2,5 a 50 µm
4000 a 400 cm-1
50 a 100 µm
4
La regione dell’INFRAROSSO MEDIO va da 4000 a 400 cm−1
La regione più interessante dal punto di vista analitico è il
MIR, perché da informazioni sulla struttura dei composti.
IR medio
2,5 a 50 µm
4000 a 400 cm-1
5
CHE COSA MISURA LO STRUMENTO ?
Lo strumento opera irradiando un campione con radiazioni
IR a diversa frequenza (nella regione 4000 ÷ 400 cm-1)
Radiazione
(hv)
1 sola frequenza
è stata assorbita
Successivamente misura :
La FREQUENZA delle radiazioni che
assorbite e di quelle che vengono trasmesse.
vengono
6
CHE COSA MISURA LO STRUMENTO ?
La FREQUENZA delle radiazioni che
assorbite e di quelle che vengono trasmesse.
vengono
7
La DIMINUZIONE dell’INTENSITA’ della radiazione IR
assorbita:
INTENSITA’ (o AMPIEZZA della radiazione IR)
Intensità della radiazione incidente
Intensità della radiazione risultante
dopo l’assorbimento
Mentre LUNGHEZZA D’ONDA e FREQUENZA della radiazione non
8
cambiano.
LO SPETTRO INFRAROSSO
Lo spettro IR si presenta come un GRAFICO in cui vengono
riportate:
Nell’asse delle ascisse la frequenza delle radiazioni IR assorbite
espressa in numero d’onda (wavenumbers)
In ordinate è riportata la % di trasmittanza (%T) cioè la % di
radiazione incidente che passa attraverso il campione senza essere
assorbita (ovvero la % di radiazione trasmessa).
Lo spettro si presenta come una serie di bande più o meno intense
9
ordinate
ordinate
Lo Spettro Infrarosso
Trasmittanza IR
- T% del 100% significa che tutta l’energia ha attraversato il campione
senza essere assorbita
- una bassa T% significa che parte dell’energia è stata assorbita dal
campione
10
Lo Spettro Infrarosso
Frequenza e Numero d’onda
ascisse
ascisse
Numero d’onda ν = 1/λ
espresso in cm-1
11
Lo Spettro Infrarosso
Perché si usa il numero d’onda?
ν = 1/λ
Numero d’onda
Per convertire
espresso in cm-1
∼ν
λ
λ = 5 . 10-4 cm
∼ν
=
1
5 . 10-4 cm
1 . 104 cm
5
=
Talvolta negli spettri
IR o nelle tabelle sono
riportati i valori di λ
= 2000 cm -1
Vantaggio nell’uso dei numeri d’onda è che sono direttamente
proporzionali all’energia E ed alla frequenza della radiazione
assorbita (vedi file “la radiazione elettromagnetica” diap. 12-13):
ν~ =
ν
c
E = hν
ν~ =
E
hc
12
INTRODUZIONE
La natura delle vibrazioni molecolari
13
Descrizione classica
PREMESSA
VIBRAZIONI MOLECOLARI
Gli atomi legati fra di loro da legami covalenti NON sono
FISSI, ma sono in continua vibrazione. La lunghezza e gli
angoli dei legami cambiano continuamente per via di queste
vibrazioni
14
Quando una molecola assorbe la radiazione infrarossa si ha
un AUMENTO* della vibrazione dei legami
* Aumenta l’ampiezza della vibrazione
15
Le radiazioni IR possono amplificare le naturali
OSCILLAZIONI delle distanze interatomiche e degli angoli di
legame nelle molecole
Il legame che congiunge i due atomi si stira e si contrae un
po’ di più!
Radiazione
(hv)
…in che modo possono vibrare le molecole?
16
MODI DI VIBRAZIONE
17
Tipi di vibrazione
Tipi di vibrazione
Tutti i movimenti possono essere descritti in termini di 2
TIPI di vibrazioni molecolari.
stiramento
(stretching)
piegamento
(bending)
18
Stiramento (stretching)
Tipi di vibrazione
I. Lo stiramento o stretching, produce un cambiamento nella
lunghezza del legame.
Lo stiramento è un movimento ritmico lungo la linea che
unisce gli atomi, sicchè la distanza interatomica è
aumentata o ridotta.
19
Stiramento (stretching) -CH2
Tipi di vibrazione
I. Lo stiramento o stretching, produce un cambiamento nella
lunghezza del legame.
Stiramento
Stiramento
simmetrico
asimmetrico
Vibrazione simmetriche (s) avvengono conservando completamente la simmetria molecolare
Vibrazione asimmetriche (as) avvengono con perdita di uno o più elementi di simmetria
20
Piegamento (bending) -CH2
Tipi di vibrazione
Il. Il piegamento o bending, risulta in un cambiamento
dell’angolo di legame. Queste vibrazioni vengono chiamate
scissoring, rocking, twisting o "wig wag" motions.
21
Piegamento (bending) -CH2
Tipi di vibrazione
Il. Il piegamento o bending, risulta in un cambiamento
dell’angolo di legame. Queste vibrazioni vengono chiamate
scissoring, rocking, twisting o "wig wag" motions.
..nel piano
Piegamento
scissoring
Piegamento
rocking
22
Piegamento (bending) -CH2
Piegamento
wagging
Tipi di vibrazione
Piegamento
twisting
..fuori dal piano
23
24
Come vengono indicati i tipi di movimento sullo spettro IR
Stretching
simmetrico
νs CH2
Bending nel piano Bending nel piano
o scissoring
o rocking
δs CH2
ρ CH2
Stretching
antisimmetrico
νas CH2
+ = piegamento sopra il piano del foglio
- = piegamento sotto il piano del foglio
Bending fuori dal piano Bending fuori dal piano
o wagging
o twisting
ω CH2
τ CH2
25
Sullo spettro, in corrispondenza dei picchi, si indicano il
gruppo funzionale ed il tipo di vibrazione con le lettere
greche
ω
νs
δs
ρ
νas
26
Modi di vibrazione
QUANTI SONO I MODI DI VIBRAZIONE POSSIBILI IN UNA MOLECOLA?
…..QUANTE BANDE DI ASSORBIMENTO SI OSSERVANO?
27
Gradi di libertà di una molecola
Modi di vibrazione
Ogni atomo, riferendosi ad una terna (x, y, z) di assi
cartesiani, possiede 3 coordinate spaziali (gradi di libertà),
cioè può muoversi nelle tre direzioni dello spazio x, y, z.
La molecola ne possiede quindi 3n gradi di libertà totali (n =
numero di atomi). Questo valore comprende tutti i possibili
movimenti della molecola:
3
3n
28
Modi di vibrazione
Se ai gradi di libertà totali togliamo i gradi di libertà
traslazionali e rotazionali…
Gradi di libertà traslazionali: la molecola si comporta come un
corpo rigido il cui baricentro si sposta lungo i tre assi, la molecola
presenta 3 gradi di libertà (sono necessarie 3 coordinate per
descrivere la traslazione).
Gradi di libertà rotazionali: la molecola ruota intorno ai tre assi; per
le molecole lineari i gradi di libertà sono 2 (perché la molecola è
bidimensionale), per le altre sono 3.
2 coordinate θ e φ
3 coordinate θ, φ e Ψ
29
…restano i gradi di libertà vibrazionali…..
Modi di vibrazione
Gradi di libertà Vibrazionali: sono 3n-(3+3). Per le molecole
lineari sono 3n-(3+2),
Gradi di libertà totali
Gradi di libertà + Gradi di libertà
Gradi di libertà
- traslazionali
della molecola
rotazionali
Vibrazionali =
3n
3
3 oppure 2
30
Modi di vibrazione
Riassumendo: modi di vibrazione possibili
Nel caso di una molecola che contenga N atomi, vi sono:
Tipo di molecola
Formula modi normali
Modi di v. in una
molecola di 3 atomi
Lineare
3N-5
4
Non lineare
3N-6
3
All’aumentare del numero di atomi (N) aumentano i modi
possibili di vibrazione.
31
…qualche esempio
Modi di vibrazione
Molecole biatomiche
Hanno un unico modo di vibrazione, nel quale i due atomi
oscillano lungo una direzione o grado di libertà x
(stiramento) mentre il centro di massa rimane stazionario.
3n-5
3 x 2-5 = 1
32
Modi di vibrazione
Molecole poliatomiche
3n-6 (-5 se lineare) vibrazioni possibili:
Modi di
vibrazione
H2O
(3 x 3) -6
3
Formaldeide
CH2O
(3 x 4) -6
6
Etanolo
C2H6O
(3 x 9) -6
21
Acqua
33
Modi di vibrazione
Acqua
v = 3756 cm-1
H2O;
3 modi normali di vibrazione
v = 3652 cm-1
v = 1545 cm-1
34
Modi di vibrazione
Formaldeide, H2C=O tetratomica, può avere 3 × 4 − 6 = 6
modi normali di vibrazione
Gas Phase Infrared Spectrum of Formaldehyde, H2C=O
ω
νs
δs
ρ
νas
35
Modi di vibrazione
Da quanto detto si potrebbe dedurre che:
Il numero dei modi di vibrazione (3n-5) di una molecola
corrisponda al numero di bande osservate nello spettro IR
Es. Etanolo
C2H6O
n=9
21
?
36
Non tutte le (3n-5 )vibrazioni di una molecola possono essere
osservate all’IR
Valore indicativo
QUALI VIBRAZIONI VENGONO REALMENTE OSSERVATE ALL’IR?
…IR ATTIVE?
37
REGOLE DI SELEZIONE =
condizioni necessarie per l’assorbimento
DESCRIZIONE DEL FENOMENO:
interazione della molecola con la radiazione IR
38
Ia Regola di selezione:
Regola di selezione del momento di dipolo
39
Descrizione del fenomeno secondo la meccanica classica:
Il modello ondulatorio della radiazione elettromagnetica
La teoria classica considera la radiazione elettromagnetica
come costituita da un onda elettrica e un onda magnetica
oscillanti in fase su piani perpendicolari tra loro
40
Figura 1. Rappresentazione ondulatoria di una radiazione elettromagnetica
Meccanica classica
La componente elettrica della radiazione
E’ la componente elettrica della radiazione elettromagnetica
che interagisce con la materia e promuove l’assorbimento
infrarosso.
E
Vettore
elettrico
41
Meccanica classica
La componente elettrica della radiazione
L’oscillazione dell’onda elettromagnetica è accompagnata
da un cambiamento periodico del segno: + → - → + → -….
Figura.
Figura. Andamento della polarità
polarità del vettore elettrico
42
Meccanica classica
Cosa succede quando questo vettore elettrico con polarità
oscillante (+ → - → + ...) incontra una molecola?
Consideriamo la molecola di HCl:
Complessivamente non possiede carica elettrica
tra Cl e H esiste una differenza di elettronegatività
43
Differenza di elettronegatività H vs Cl
Meccanica classica
Pauling electronegativity
3.0
2.1
δ-
δ+
Accumulo di densità elettronica sul Cl
(parziale carica negativa, δ-)
Carenza di densità elettronica sul H
(parziale carica positiva, δ+)
44
Meccanica classica
HCl contiene due cariche separate da una distanza!
δ-
d
δ+
Tale fenomeno è noto come momento di dipolo:
Il momento di dipolo è una misura della distribuzione
assimmetrica della carica di una molecola
45
Meccanica classica
Momento di dipolo
µ=q×r
µ è il momento di dipolo
q è la carica (q+
(q+ + q-)
r è la distanza di separazione q+ ↔ qq-
Il momento di dipolo è una grandezza vettoriale* (→)
momento di dipolo
-
+
* Le grandezze vettoriali vengono rappresentate da frecce:
46
Meccanica classica
La VIBRAZIONE NATURALE della molecola di HCl, prima
cioè che sia soggetta all’azione della radiazione IR, fà
variare periodicamente la distanza r tra i 2 atomi.
ricorda
µ=q×r
∆µ ≠ 0
r
Ciò produce una variazione periodica (oscillazione) del
momento di dipolo della molecola µ.
La vibrazione della molecola produce un CAMPO ELETTRICO
OSCILLANTE.
47
Meccanica classica
Il meccanismo di assorbimento consiste nell’INTERAZIONE
tra:
il campo elettrico della radiazione elettromagnetica
il campo elettrico oscillante del dipolo molecolare
48
Meccanica classica
L’ assorbimento è vincolato al verificarsi di due condizioni:
1) L’assorbimento si verifica se i due campi oscillanti hanno la
stessa FREQUENZA. (Condizione necessaria ma non sufficiente!)
2) La molecola può entrare in risonanza con la radiazione solo se
la sua vibrazione produce un dipolo oscillante (variazione di µ)
∆µ ≠ 0
H-Cl
Livello fondamentale
+
Photon
Energia = hν
H-Cl
Livello vibrazionale eccitato
Se sono soddisfatte le 2 condizioni, l’energia della radiazione
elettromagnetica è trasferita alla molecola come moto vibrazionale,
49
aumentando l’AMPIEZZA della vibrazione naturale.
Meccanica classica
L’assorbimento dell’energia della radiazione elettromagnetica
porta ad un aumento dell’AMPIEZZA della vibrazione naturale,
mentre la FREQUENZA naturale di oscillazione viene
conservata.
Le vibrazioni diventano più ampie e anche più rapide perchè
le masse devono muoversi più velocemente per conservare la
stessa frequenza di oscillazione
50
Momento di dipolo
Regola di selezione del momento di dipolo
Non tutti i MODI NORMALI di vibrazione sono attivi all’IR:
non tutte le (3n-5) o (3n-6) vibrazioni di una molecola possono essere
osservate all’IR
Valori indicativi
Perché una vibrazione sia ATTIVA (cioè ci sia trasferimento
di energia dalla radiazione alla molecola) deve VARIARE IL
MOMENTO DI DIPOLO della molecola nel corso della
vibrazione.
1° Regola di selezione
∆µ ≠ 0
51
Momento di dipolo
molecole biatomiche omonucleari (simmetriche)
Possiedono 1 solo modo di vibrazione (I movimenti di
bending non sono possibili in molecole formate da 2 soli
atomi)
3n-5
3 x 2-5 = 1
H–H
N ≡N
O2
Se la molecola biatomica è formata da due atomi uguali
come quella dell’azoto N2 o dell’idrogeno H2 il momento
dipolare è nullo (µ = 0) e non può variare per effetto della
vibrazione dei due nuclei. Quindi non assorbono
nell’infrarosso.
52
Momento di dipolo
molecole biatomiche eteronucleari
δ+
3n-5 = 1
δ-
Le molecole eteronucleari come per esempio l’ossido di
carbonio o l’acido cloridrico, hanno sempre un momento
dipolare µ ≠ 0 (un atomo è sempre più elettronegativo
dell’altro). µ può variare durante la vibrazione e quindi la
53
transizione è attiva nell’infrarosso.
Abbiamo visto che la radiazione elettromagnetica può
interagire con una molecola di HCl che possiede un momento
di dipolo permanente
momento di dipolo
-
+
Le molecole che non possiedono un momento di dipolo
permanente possono interagire con la radiazione
elettromagnetica?
54
molecole triatomiche simmetriche
Momento di dipolo
La molecola CO2, triatomica e lineare, può avere 3 × 3 − 5 = 4
modi normali di vibrazione.
La CO2 è una molecola lineare debolmente polarizzata: la
carica elettrica è distribuita con un leggero eccesso sui 2
ossigeni terminali.
µ1
µ2
µ = µ1 + µ2 = 0
I 2 dipoli (µ1 e µ2) associati a ciascun legame C=O hanno ugual
direzione con verso opposto e quindi si elidono l’un l’altro
La molecola di CO2 non possiede un momento di dipolo
55
permanente…….
3 × 3 − 5 = 4 modi normali di vibrazione
Quali di queste vibrazioni sono attive all’IR?
56
Modi otticamente INATTIVI della CO2
La vibrazione di stretching simmetrico della CO2 non è
attiva all’IR perché non comporta variazione del momento
di dipolo durante la vibrazione, che rimane nullo. ∆µ=0
l'entità dello spostamento degli O rispetto al C centrale
è sempre la stessa, quindi anche se le distanze
variano, la somma vettoriale dei momenti dipolari è
sempre nulla!
µ1 + µ2 = 0
(r = 0, ∆µ = 0)
I 2 dipoli C=O quando la vibrazione è simmetrica si
continuano a bilanciare in ogni momento dello
stiramento.
57
Modi otticamente ATTIVI della CO2
Lo stiramento asimmetrico produce un assorbimento della
radiazione:
Si crea periodicamente un dipolo elettrico di segno alterno
(r ≠ 0, ∆µ ≠ 0)
Stiramento assimmetrico. Fluttuazione del momento di dipolo
Poiché una distanza C=O si allunga e l'altra si accorcia si genererà una consistente
variazione del momento dipolare
58
Modi otticamente ATTIVI della CO2
Nella vibrazione di piegamento la molecola addotta
periodicamente una struttura non lineare in cui il dipolo elettrico
non è nullo.
(r ≠ 0, ∆µ ≠ 0)
Vibrazione di bending. Fluttuazione del momento di dipolo
59
Abbiamo 2 forme di BENDING (Vibrazione di piegamento ):
uno si verifica sul piano, prevista a 667 cm-1, cioè ad una frequenza
molto bassa
l'altro che si attua al di fuori del piano anch'esso a 667 cm-1.
O C O
O C O
Piegamento (degenere)
Se osserviamo bene questi due moti sono DEGENERI poiché sono
perfettamente equivalenti, anche se avvengono su 2 piani diversi! Quindi non
60
possono ricevere una quantità di energia diversa!
Solo 2 dei 4 modi normali di vibrazione.
Stiramento
Simmetrico
inattivo
-Stiramento simmetrico è IR inattivo
-I due piegamenti sono degeneri (danno una sola banda)
61
Momento di dipolo
molecole triatomiche lineari non simmetriche
3n-5 = 4
O=C=S
µ≠0
La vibrazione di stretching del COS è attiva all’IR perché
comporta variazione del momento di dipolo ∆µ ≠ 0.
62
MOLECOLE TRIATOMICHE NON LINEARI
Acqua
H2O;
v = 3756 cm-1
3 modi normali di vibrazione
v = 3652 cm-1
v = 1545 cm-1
63
Momento di dipolo
molecole poliatomiche
- i legami polari, (se sono più di uno), e i doppietti elettronici
devono essere disposti in modo che i momenti di dipolo di
legame non si cancellino a vicenda
64
Momento di dipolo
molecole poliatomiche
In una molecola organica ogni singolo legame che presenti
gruppi identici sulle due estremità non assorbe al IR.
ν C-H
∆µ ≠ 0
ν C-C
∆µ = 0
Es.1. nel etano, il legame C-C non assorbe al IR perchè è
presente un gruppo metile ad entrambe le estremità. Mentre i
legami C-H metilici assorbono.
65
Momento di dipolo
Doppi e tripli legami C-C di alcheni e alchini sostituiti
simmetricamente sono inattivi
C
C
difenilacetilene
Es.2. Nel difenilacetilene il legame C≡C non da luogo ad
alcun assorbimento perché la vibrazione non può produrre
nessuna variazione del momento di dipolo.
66
IIa Regola di selezione:
Regola di selezione del numero quantico
67
Teoria quantica
Principio della QUANTIZZAZIONE DELL’ENERGIA
E’ il principio che costituisce la primaria differenza tra i sistemi del
mondo:
MACROSCOPICO, che assorbono energia in modo continuo
ATOMICO e MOLECOLARE che invece acquistano e cedono energia
solo in porzioni discrete e definite dette QUANTI.
I sistemi atomici e molecolari possono assorbire SOLO
quantità DISCRETE DI ENERGIA
68
Teoria quantica
Quantizzazione dell’energia
Consideriamo 2 oggetti simili:
E
E
Livelli eccitati
0
Livello fondamentale
0
H
2 sfere metalliche unite da una molla
F
Molecola biatomica
69
Teoria quantica
La molla può assorbire energia vibrazionale con continuità e
può aumentare l’ampiezza dell’oscillazione in modo
PROGRESSIVO
E
0
70
Teoria quantica
La molecola può assorbire energia solo per quantità discrete
(per quanti) e di conseguenza anche l’ampiezza della
vibrazione varia in modo discontinuo, vale a dire per salti, per
quantità finite
E
E
Solo un numero limitato
di livelli è permesso
0
0
H
F
71
Descrizione del fenomeno secondo la teoria quantistica
La radiazione elettromagnetica (modello corpuscolare)
La
teoria
quantistica
considera
la
radiazione
elettromagnetica come un fascio di “pacchetti di energia” –
fotoni o quanti – che si muovono nello spazio a velocità
costante (c nel vuoto). L’energia di un fotone è in relazione
con la frequenza di una radiazione elettromagnetica, per
mezzo dell’espressione:
Efotone = h ν
Frequenza ν ed energia E risultano direttamente proporzionali attraverso
la costante di proporzionalità h, detta costante di Planck (6,6 x 10-34 Js). 72
Teoria quantica
Una fotone può trasferire la propria energia ad una molecola.
H-Cl
+
Livello fondamentale
Photon
H-Cl
Energia = hν
Livello vibrazionale eccitato
Il trasferimento di energia avviene per quanti: un fotone non può
cedere parte della propria energia alla molecola; o la cede tutta, o
niente.
Campione
Radiazione
Incidente
Radiazione
Trasmessa
Detector
Sorgente IR
Fotone con E = hν
Energia assorbita
1 fotone/ 1 molecola
73
Teoria quantica
LIVELLI ENERGETICI DELLE MOLECOLE
L' energia vibrazionale della molecola è QUANTIZZATA:
QUANTIZZATA
tra due livelli contigui 1 e 2 non esistono altri possibili livelli, quindi la
molecola può avere il contenuto energetico totale che compete al
livello 1, o quello che compete al livello 2. (Non sono possibili contenuti
energetici intermedi).
E
3
2
Non esistono stati intermedi
1
0
Cosa succede se si irradia una molecola con un fotone di energia E = hν?
74
Assorbimento di energia
Teoria quantica
La molecola può assorbire l’ENERGIA della radiazione solo se questa
è UGUALE alla differenza di energia tra due livelli possibili della
molecola (solitamente lo stato fondamentale e il primo stato eccitato).
E
stato eccitato
0
stato fondamentale
75
Teoria quantica
Se si irradia una molecola con un fotone di energia E = hν uguale alla
differenza tra il livello in cui si trova la molecola e il livello di un suo
possibile stato eccitato.....
Efotone = hν = E stato eccitato - E stato fondamentale = ∆E
E
stato eccitato
0
stato fondamentale
∆E
…..la molecola può assorbire il fotone e compiere una TRANSIZIONE
passando nello stato eccitato.
76
Calcolo dell’energia dei livelli vibrazionali
La trattazione quantomeccanica completa
soluzione dell’equazione di Schroedinger.
richiederebbe
Teoria quantica
la
L'equazione di Schroedinger per l'oscillatore armonico è:
Erwin Schrödinger
(1887 - 1961)
dove l'hamiltoniano ^H è dato dalla somma dell'energia cinetica e potenziale
La soluzione è QUANTIZZATA:
≥
Dove v è la frequenza di oscillazione
n è il numero quantico vibrazionale
77
energia dei livelli vibrazionali
L' energia vibrazionale della molecola è QUANTIZZATA ed è pari a:
a
1
E = hν N +
2
N = 1, 2, 3, .....
N è il numero quantico vibrazionale
78
La molecola può compiere una TRANSIZIONE se l’energia della
radiazione (E = hν) uguale alla differenza (∆E ) tra il livello in cui si trova
la molecola e il livello di un suo possibile stato eccitato
∆E = h ν
∆E
∆E = 3/2 hν - 1/2 hν = hν
79
Affinché una radiazione possa essere assorbita da un
campione, non è sufficiente che venga soddisfatta
l’equazione di Plank. (energia della radiazione =
differenza di energia tra due livelli energetici del
campione:
∆E = h ν
80
Regola di selezione per il numero quantico
Sono IR attive solo quelle transizioni tra livelli vibrazionali
ADIACENTI, cioè per i quali:
∆N = ±1
(2° regola di selezione)
(segno positivo corrisponde all’assorbimento
e quello negativo all’emissione)
∆N
Radiazione
(hv)
81
Due sono le differenze fra l’oscillatore quantistico e quello
classico
1) le energie permesse al sistema sono solo quelle corrispondenti ai diversi
valori discreti (1/2 hν; 3/2 hν…) del numero quantico vibrazionale e separate
fra di loro della quantità costante hν.
2) l’energia minima corrispondente al numero quantico N = 0 non è nulla, ma
vale ½ hν , quantità che viene appunto denominata energia del punto zero. In
altri termini la vibrazione molecolare NON SI ARRESTA al punto di equilibrio,
neppure allo zero assoluto.
energia del punto zero
82
Assorbimento e conservazione dell’energia della radiazione
H-Cl
+
Livello fondamentale
Photon
Energia = hν
H-Cl
Livello vibrazionale eccitato
Energia = hν
Figura.
Figura. Come una molecola passa al livello vibrazionale eccitato.
eccitato.
A) Prima che radiazione e molecola interagiscano, la radiazione
possiede energia E = hcv
B) Dopo che radiazione e molecola interagiscono, il fotone è
assorbito dalla molecola di HCl come moto vibrazionale (l’energia è
conservata)
83












