Forza elettrostatica

Forza elettrostatica
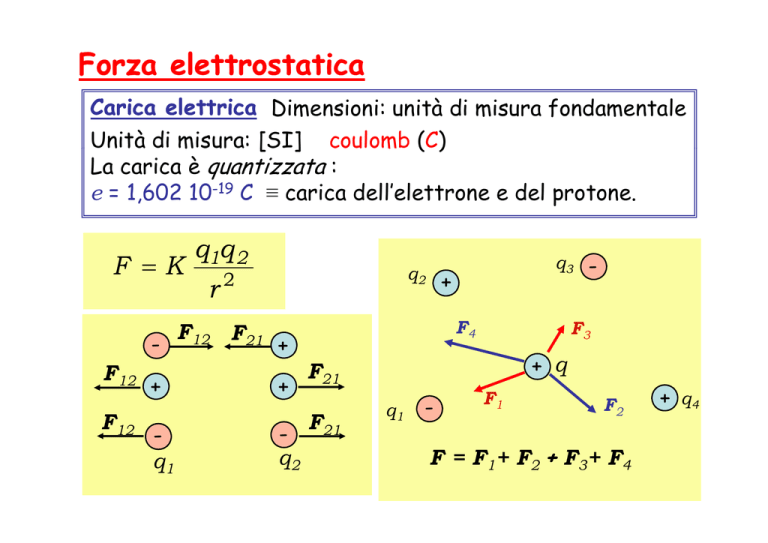
Carica elettrica Dimensioni: unità di misura fondamentale
Unità
n tà di m
misura:
sura [S
[SI]] cou
coulomb
om ((C))
La carica è quantizzata :
e = 1,602 10-19 C ≡ carica dell’elettrone e del protone.
F =K
F12
F12
+
q1
q1q 2
q2
r2
F12 F21
+
+
q2
q3
+
F4
F3
+ q
F21
F21
-
q1
-
F1
F2
F = F1+ F2 + F3+ F4
+ q4
Il campo elettrico
q2
+
• La forza F dipende
anche da q.
F4
U ità di misura:
Unità
i
[SI]
-
F3
+ q
• Il rapporto F/q dipende
solo dalla distribuzione
delle cariche qi
Campo Elettrico:
q3
q1
-
F1
F = F1+ F2 + F3+ F4
n
Fi
F
⇒E =∑
E =
q
i q
N/C
F2
+ q4
Linee di forza di una carica positiva
Un modo
U
m d di visualizzare
is li
i campi
m i di f
forze.
Linea di forza ≡ curva la cui tangente in ogni punto
ha la stessa direzione della forza in quel punto.
punto
Forza agente
F
t sulla
s ll carica
i di
prova +q0 in presenza della
carica +q
Li
Linee
d
dell campo E prodotto
d
dalla carica +q.
Semirette uscenti da q
Linee di forza del campo E di una
carica negativa
Semirette entranti in -q.
Il numero di linee di forza del
campo E che attraversano
perpendicolarmente una
superficie, diviso per l’area
della superficie,
p
,è
proporzionale al modulo di E.
Nota Bene: Le linee di forza NON esistono, i campi SI!
Linee di forza del campo elettrico di
due cariche uguali
Le linee di forza del campo E sono curve regolari e continue tranne nei
punti in cui sono localizzate le cariche; qui le linee iniziano o terminano
a seconda che la carica sia positiva o negativa.
Potenziale elettrico
L rA →rB
⎛1 1⎞
= KQq
KQ ⎜⎜ − ⎟⎟
⎝ r A rB ⎠
kQq
EPE =
r
EPE dipende anche da q.
EPE /q dipende solo dalla distribuzione delle cariche Qi
Potenziale Elettrico:
Unità di misura: [[SI]]
Q
EPE
= K ⇒V =
V =
q
r
volt ((V):
)
1V=1J/C
Qi
∑i K r
i
n
L’elettronvolt
L
elettronvolt
Altra unità di misura dell’energia
elettronvolt (eV) ≡lavoro necessario per spostare un
elettrone tra due punti tra cui ΔV= 1 V
(
)
1 eV = 1,602 × 10 −19 C × (1 V ) = 1,602 × 10 −19 J.
1 KeV= 103 eV
1 MeV= 106 eV
1 GeV=
GeV 109 eV
Variazione dell’Energia Potenziale elettrica
C si possibili
Casi
p ssibili di sp
spostamento
st m t di una q2 in
i p
presenza
s
di q1
⎛1
1 ⎞
Lr A →rB = KQq
Qq ⎜⎜ − ⎟⎟
⎝ rA rB ⎠
q1
q1
q1
q1
+
q2
F
+
L<0
q2
-
+
+
-
q2
+
+
L>0
F
F
L>0
q2
L<0
-
EP cresce
-
EP decresce
+
EP decresce
+
EP cresce
F
Superfici equipotenziali
Superficie equipotenziale ≡ superficie sui cui punti il
potenziale elettrico è lo stesso.
carica +q
carica -q
Non si esegue un lavoro per spostare una carica su una
superficie equipotenziale.
Il campo E è sempre perpendicolare alle superfici
equipotenziali.
Come si genera il battito cardiaco
ELETTROCARDIOGRAMMA
Applicazioni mediche di differenze di potenziale
elettrico
La superficie del corpo umano non
è una superficie
fi i equipotenziale.
i
i l
Fra i varii punti
F
ti d
dell corpo cii sono
piccole differenze di potenziale
(circa 30÷500 μV).
Q
Queste
differenze costituiscono
la base per esami quali:
l’elettrocardiografia,
l elettroretinografia,
l’elettroretinografia,
l’elettroencefalografia
Elettrocardiografia
g
Elettroretinogrfia
Elettroencefalografia
Potenziale di azione
++++++++++++++
--------------------A
--------------------++++++++++++++
++++++--++++++
----------++--------++
--------++A------++++++--++++++
E = 108 N/C
Vi-Ve (mV)
potenziale
d’azione
50
0
+++++-----++++
------++++----------++++A-----+++++----+++++
++++--++--+++
-----++--++---A ---------++--++
+++++--++--+++++
impulso
impulso
potenziale
di riposo
-50
-100
0
05
0.5
10
1.0
15
1.5
t (ms)
V l ità di ttrasmissione
Velocità
i i
= 25
25m/s
/
Il modello atomico di Bohr
Nel modello di Bohr dell’atomo
dell atomo di idrogeno l’elettrone
l elettrone
ruota attorno al protone nucleare su un orbita
circolare di raggio r=5,3.10-11 m. Si determini il
potenziale elettrico che il protone genera a questa
distanza, l’energia potenziale dell’elettrone e la sua
energia cinetica.
EP = eV = eK
v=
2
p
−19
e
9 1,6 × 10
V = K = 9 ×10
= +27,2 V.
−
11
r
5,3 ×10
Soluzione
F =K
e
e
= -1,6 ×10−19 × 27,2 = −4,35 ×10−18 J = −27,2 eV.
r
e2
r
2
v2
=m
r
9
(
1 2 1 e2
mv = K
= 13,6eV
2 r
2
⇒
)
−19 2
9×10 × 1,6×10
Ke
6
=
2
,
18
×
10
m s. (vedi Esempio 11-4)
=
−
31
−
11
mr
9,11×10 ×5,3×10
Energia di ionizzazione
Energia di legame W di un elettrone
in un atomo ≡ minima energia
g
necessaria per separare l’elettrone
dall’atomo (ossia per portarlo a
di t
distanza
iinfinita).
fi it )
Per l’atomo di idrogeno:
1 2
e2
E = EC + EP = mv − Ke
r
2
(
)
(
)
2
−19
1
−31
6 2
9 1,6 ×10
−19
= 9,11×10 2,18 ×10 − 9 ×10
=
−
21
,
8
×
10
J
−10
2
0 53×10
0,53
W = −E = 21,8
21 8 × 10-19 J = 13,
13 6 eV
Esempio: L’anodo (elettrodo positivo) di un tubo per raggi X è al
potenziale V=125000 V rispetto
p
p
al catodo ((elettrodo negativo).
g
)
(a) Quanto lavoro viene compiuto quando un elettrone viene
accelerato dal catodo all’anodo?
(b) Se ll’elettrone
elettrone è inizialmente in quiete
quiete, quanta energia cinetica ha
l’elettrone quando arriva all’anodo?
14 J = 125 k
S l i
Soluzione:
((a)) 2
2,0
0.10-14
keV
V
(b) 2,0.10-14 J = 125 keV
Esempio: Determinare la forza R (in modulo, direzione e verso) che si
esercita su una carica positiva di intensità Q=2.10-6 C, situata al centro
di un quadrato il cui lato ha lunghezza L=20 cm
cm, da parte di quattro
cariche tutte di intensità q= 5.10-6 C poste ai vertici del quadrato stesso.
Si determini tale forza per la seguente sequenze di segni delle cariche
q: (a) ++++, (b) ----, (c) +--+, (d) ++--.
Soluzione
q1 +
q1 - q2
+ q2
( )
(a)
(b)
F4
F3
F2
F1=F2=F3=F4
F1=F2=F3=F4
F1
+
R=0
R=0
+
Q
Q
F2
F1
F4
F3
+
+q
q4
q
4
q3
3
q1 +
q
+ 2
q1 +
- q2 (d)
F1=F2=F3=F4=
F4
F2
(c)
Q
2
=2KQq/L
F1=F2=F3=F4
+
Q +
F4
F3
R =0
R = 8F1
F2 F1
F3
F1
+q
q3 Qq
q4
q
4
= 4 2K 2
3
R
L
Esempio: Si determini il campo elettrico E ed il potenziale V nella
posizione
i i
d
della
ll carica
i Q per le
l seguenti
ti di
distribuzioni
t ib i i d
delle
ll cariche:
i h
(a) ++++, (b) ----, (c) +--+, (d) ++--.
q1 +
(a)
F4
F1=F2=F3=F4
R=0
+
E=0
Q
q
F2
V = +4 2 K
L +
q3
((c))
q1 +
F4
F1=F2=F3=F4
F3
F1
+q
4
- q2
F2
E =0
q3 -
F3
F1
(b) F1=F2=F3=F4
R =0
E =0
F1
q
V = -4 2K
L
F3
4
V =0
F2
+
-
Q
F4
q3
q1 +
(d) F1=F2=F3=F4
E = 4 2K
+q
- q2
q1 -
R = 8 F1
Q +
R =0
V =0
+ q2
2
L
-
q3
q4
+
q2
Q
F3
q
-
+
F2 F1
R
F4
-
q4
Esempio: Con riferimento alla
situazione in figura
g
(q1= 8,0
, nC,,
q2 = -8,0 nC), calcolare il campo
ed il potenziale elettrico nei
punti A e B
B.
0,4 m
q1
02m
0,2
A
0,2 m
B
q2 x
Soluzione
−9
8,0 × 10 −9
9 − 8, 0 × 10
V = 9 × 10
+ 9 × 10
= 0 V.
0, 40
0, 40
9
punto A
8,0 × 10 − 9
E1 = E 2 = 9 × 10
;
−2
16 × 10
9
E = 2 E1 = 9 × 10 2 N/C con verso da q1 a q2
−9
8,0 × 10 − 9
9 − 8, 0 × 10
V = 9 × 10
+ 9 × 10
= − 240 V
0,60
0, 20
9
punto B
−9
8,0 × 10 − 9
9 8, 0 × 10
2
E1 = 9 × 10
=
200
N/C;
E2
=
9
×
10
=
18
×
10
N/C;
−2
−2
36 × 10
4 × 10
E = E1 + E2 = 20 × 10 2 N/C con verso da q1 a q2
9
Esempio: Con riferimento alla
situazione in figura
g
(q1=3,0
, μ
μC,, q2
=-4,0 μC, q3 = -7,0 μC), calcolare
la forza elettrostatica che
agisce sulla carica q1, il campo e
il potenziale elettrico nella
posizione di q1.
0,2 m
q2
F12
Soluzione
−6
q 1q 2
× 4,0 × 10 −6
9 3,0 × 10
F12 = K 2 = 9 × 10
= 2,7 N
2
r122
0,20
F13 = K
q 1q 3
2
r13
0,15 m
q1
q3
q1
3,0 × 10 −6 × 7,0 × 10 −6
= 9 × 10
= 8,4 N
2
0,15
9
F = F12 + F13 ⇒ F = (− 2,7 N ) + (+ 8,4 N ) = +5,7 N.
E = E2 + E3
⎛ − 2,7 N ⎞ ⎛ + 8,4 N ⎞ + 5,7 N
6
E=⎜
+
=
=
+
1
,
9
×
10
N C.
⎟
⎟
⎜
−6
−6
−6
⎝ 3 × 10 C ⎠ ⎝ 3 × 10 C ⎠ 3 × 10 C
V=K
q
q2
7 ⎞
⎛ 4,0
+ K 3 = −9 × 10 9 × 10 −6 ⎜
+
⎟ = −603 × 10 3 V
r12
r13
⎝ 0,20 0.15 ⎠
x
F13
Esempio: Le superici interna ed esterna di una membrana cellulare
portano rispettivamente
p
p
una carica negativa
g
e una carica positiva.
p
A
causa di queste cariche tra le superfici della membrana esiste una
differenza di potenziale di circa 95 mV. Lo spessore della membrana
è 7,5
7 5 nm
nm. Quanto vale il modulo dell’intensità
dell intensità del campo elettrico nella
membrana?
EPe − EPi Fe ⋅ s
Ve − Vi =
=
= E ⋅s = E ×s
q
q
Ve −Vi 95 ×10−3
7 N
E=
=
=
1,27
×
10
C
s
7,5 ×10−9
Quesito: Una sferetta di carbonio ha massa m= 1 g.
Q
Quanti
ti elettroni
l tt
i possiede
i d lla sferetta?
f
tt ?
Il carbonio ha massa atomica 12 e numero atomico Z = 6.
Quindi 12 g di carbonio, cioè una mole, contengono
6 02.1023 atomi,
6,02
t mi ovvero
vver 6 vvolte
lte ttanti
nti elettr
elettroni.
ni
Il numero di elettroni in 1 g di carbonio è quindi
quindi:
(
)
1
6 × 6,02 × 10 23 = 3,01× 10 23
12
Esempio Due sferette di carbonio di massa m= 1 g sono dotate di
cariche negative identiche e sono sospese a due fili di 10 cm di
lunghezza. Dopo che sono state applicate le cariche alle due sferette, i
fili formano tra di loro un angolo di 60˚. (a) Qual’è la forza
elettrostatica tra le due sferette?
f
((b)) q
quanti elettroni sono stati
aggiunti a ciascuna sferetta? (c) Qual’è la forza di gravita tra le due
sferette?
M
(a) F = Mg
Soluzione
q1q 2
(b) F = K
=
L2
=K
565 × 10 - 5
9 × 10 9
q 12
L2
3
= 980
⇒ q1 = q 2 =
1,73
7,9 × 10 −8
11
ne =
=
4
,
9
×
10
1,6 × 10 −19
FG = G
M2
2
L
= 6,67 × 10 −8
12
10
2
60˚
L
F
L
K
0 ,10
0 = 7,9 × 10
0 − 8 C.
C
((c))
= 565 dine.
T
F
q2 -
- q1
Mg
= 6,67 ×10 −10 dine.
T
F
60˚Mg
60