Lezione del 07.03.2016
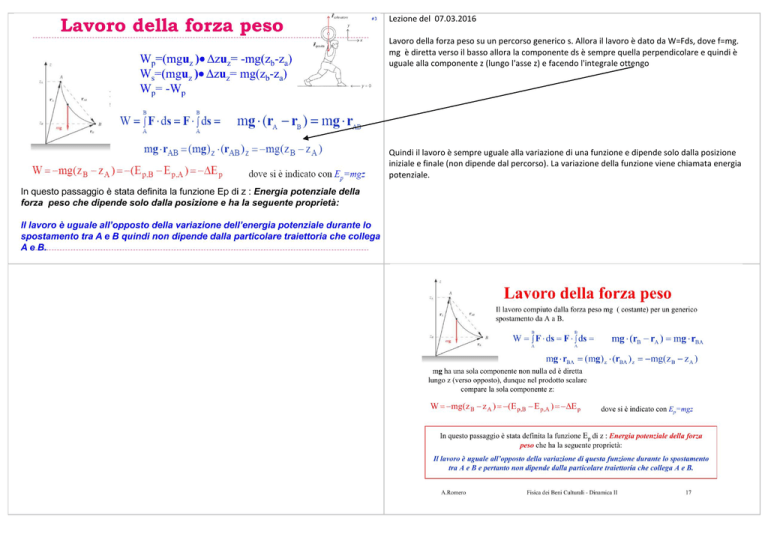
Lavoro della forza peso su un percorso generico s. Allora il lavoro è dato da W=Fds, dove f=mg.
mg è diretta verso il basso allora la componente ds è sempre quella perpendicolare e quindi è
uguale alla componente z (lungo l'asse z) e facendo l'integrale ottengo
Quindi il lavoro è sempre uguale alla variazione di una funzione e dipende solo dalla posizione
iniziale e finale (non dipende dal percorso). La variazione della funzione viene chiamata energia
potenziale.
(Walker, pag 172)
Il lavoro fatto dalla forza peso fatto in un ciclo (cioè percorrendo il percorso ABCD una volta) è pari
a 0.
Quando il corpo sale il lavoro è -mgh, quando scende è mgh; nel tratto CD e AB, essendo
perpendicolare, il lavoro è pari a 0.
Il lavoro effettuato da un sollevatore di pesi: se solleva partendo dai suoi piedi verso la testa o fa la
stessa cosa messo sopra una pedana alta 1 metro, il lavoro è lo stesso perchè quello che definiamo
è la variazione della energia potenziale tra un punto ed un altro (quindi energia potenziale tra due
punti)
Se voglio esprimere l'energia potenziale in un punto allora devo calcolare l'energia potenziale in
quel punto e dire in che sistema di riferimento mi trovo.
Anche questa funzione è una funzione che dipende dalla coordinate (e non dal percorso).
L'energia potenziale per la forza peso è diversa dalla energia potenziale della forza elastica e
l'unica cosa che hanno in comune è che il lavoro fatto per spostare un punto è uguale e contrario
alla variazione della funzione in esame.
Il sistema di riferimento che converrà usare con la molla (forza elastica) è quello in cui lo 0
corrisponde alla lunghezza della molla a riposo.
Tirando la molla, succede che faccio un lavoro che viene immagazzinato dalla molla che sarà
2
1/2kx , e tale lavoro poi si trasformerà in energia cinetica e che farà si che la molla possa
muoversi.
L'energia cinetica è anche essa espressa come una variazione (è calcolata con un integrale) ed è
2
1/2mv ed essendo una quantità al quadrato è sempre positiva e non abbiamo bisogno di un
sistema di riferimento, mentre per l'energia potenziale si ha bisogno di un sistema di riferimento.
La forza peso e la forza elastica si chiamano anche forze conservative.
Un modo per vedere se sono conservative è calcolare il lavoro e verificare che esso non dipenda
dal percorso.
Le tre definizioni sono equivalenti: la b e la c derivano dalla a. Di norma conviene dare la prima
definizione in quanto le altre due derivano da esse.
L'energia cinetica vale per tutte le forze.
L'energia potenziale vale solo per quelle forze per cui il lavoro non dipendono da un percorso
Il lavoro del cuore è una energia potenziale.
Un sistema sottoposto solo ad una o due forze è un sistema isolato.
LA forza di attrito è data da µ·N (che è una costante e la posso tirare fuori dall'integrale) nella
direzione dello spostamento utds. Ma ut è il versore di modulo 1 nella direzione dello
spostamento, ed è parallelo al vettore ds, per cui utds=1. (ds è il trattino infinitesimo).
Ora non avrò più lo scalare e l'integrale γ lungo il percorso di ds non è altro che la lunghezza dello
spostamento (e non da come prima la differenza di vettori).
La forza di attrito non è conservativa perchè il lavoro della forza di attrito dipende dal percorso
(per andare dal punto iniziale al punto finale) e allora non posso esprimere una energia potenziale.
Se vi è solo la forza di attrito e non altre forze allora il lavoro delle forze di attrito produce una
diminuzione di velocità (vi è dissipazione -> sistema non isolato????).
L'energia meccanica in presenza di forze conservative si conserva, se non lo fa vuol dire che vi
sono altre forze di natura dissipativa.
In un sistema isolato, l'energia si conserva e questo è vero solo in parte perchè dipenda da ciò che
si intende per sistema (se prendo un punto materiale allora si conserva, ma vale solo per il punto
materiale perchè lo inserisco in un contesto di "sistema chiuso"). Nel caso di una palla se che
rimbalza questa subirà una deformazione, quindi in qualche modo un po' di energia viene variata
(si trasforma in altra forma di energia).
Nella slide ha fatto casino con i simboli, considerare Ek = U
(min 01h 00, risentire... pag 152 halliday, pag 179 del walker)
In presenza di forze conservative, facendo il lavoro da A ad B, l'energia cinetica e potenziale
rimangono costanti; in presenza di forze non conservative facendo la differenza della somma
dell'energia potenziale e cinetica calcolata nel punto B e la somma dell'energia potenziale e
cinetica calcolata nel punto A non sarà uguale a 0 (perchè non siamo in presenza di una costante)
e mi darà il lavoro fatto dalle forze di attrito (che è la forza dissipativa)
Il principio di conservazione dell'energia è molto usato perchè semplifica i calcoli e basta vedere
l'inizio e la fine per capire se è successo qualcosa (perchè l'energia di dovrebbe conservare), senza
vedere "momento per momento" se l'energia è stata persa o meno. Se non si è conservata vuol
dire che in "mezzo" oltre alle forze conservative agiscono anche delle forse dissipative.
(serway pag 215)
Punto iniziale
Punto finale
Energia cinetica
Negli esercizi che da la prof, per trovare la velocità usare il principio di conservazione dell'energia
perchè è più facile; per trovare l'accelerazione invece è più facile usare le forze
In presenza del piano inclinato la "g" è più piccola (é gsenθ).
In presenza di forza peso:
- se il piano è liscio allora c'e' la sola presenza della forza peso
- se il piano è scabro, allora oltre alla forza peso vi è l'attrito












