Suppletiva 2013.ordinamento
PROBLEMA 2
Del trapezio ABCD si hanno le seguenti informazioni: la base maggiore AB e la base minore DC
misurano rispettivamente
e
, l’altezza del trapezio misura
e la tangente dell’angolo
è uguale a
.
1. Si calcolino le aree dei quattro triangoli in cui il trapezio è diviso da una sua diagonale e dai
segmenti che uniscono il punto medio di questa con gli estremi dell’altra diagonale.
2. Si determinino, con l’aiuto di una calcolatrice, le misure, in gradi e primi sessagesimali,
degli angoli del trapezio.
3. Riferito il piano del trapezio ad un conveniente sistema di assi cartesiani, si trovi
l’equazione della parabola Γ avente l’asse perpendicolare alle basi del trapezio e passante
per i punti B, C, D.
4. Si determinino le aree delle due regioni in cui il trapezio è diviso da Γ.
SOLUZIONE
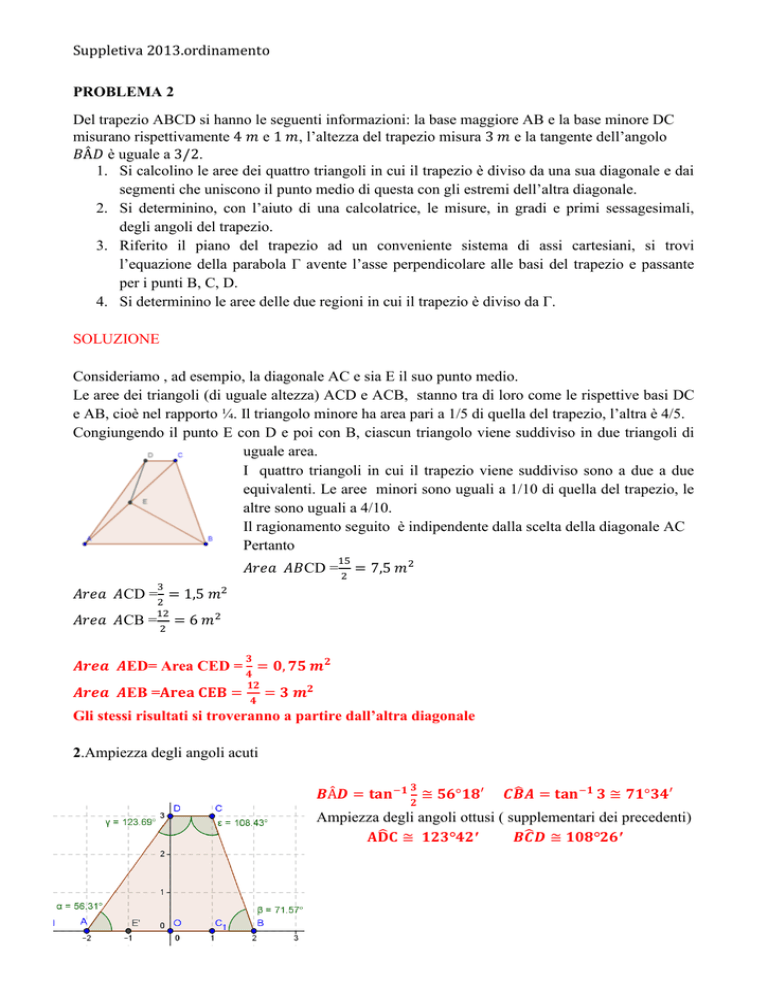
Consideriamo , ad esempio, la diagonale AC e sia E il suo punto medio.
Le aree dei triangoli (di uguale altezza) ACD e ACB, stanno tra di loro come le rispettive basi DC
e AB, cioè nel rapporto ¼. Il triangolo minore ha area pari a 1/5 di quella del trapezio, l’altra è 4/5.
Congiungendo il punto E con D e poi con B, ciascun triangolo viene suddiviso in due triangoli di
uguale area.
I quattro triangoli in cui il trapezio viene suddiviso sono a due a due
equivalenti. Le aree minori sono uguali a 1/10 di quella del trapezio, le
altre sono uguali a 4/10.
Il ragionamento seguito è indipendente dalla scelta della diagonale AC
Pertanto
CD =
CD =
CB =
ED= Area CED =
EB =
Gli stessi risultati si troveranno a partire dall’altra diagonale
2.Ampiezza degli angoli acuti
Ampiezza degli angoli ottusi ( supplementari dei precedenti)
Soluzione di Adriana Lanza
Suppletiva 2013.ordinamento
3.
Si sceglie un riferimento avente per asse x la retta AB
e per origine il punto medio del lato AB.
I vertici del trapezio assumono le seguenti coordinate
La parabola Γ , avendo per asse di simmetria
la retta
, deve passare per il simmetrico di B
rispetto alla suddetta retta, cioè per il punto E(-1;0)
La sua equazione sarà del tipo
Imponendo il passaggio per D si determina il valore del parametro a
Equazione di Γ
4 Le due regioni in cui Γ divide il trapezio , sono:
S1 triangolo mistilineo ADE, differenza fra il triangolo ADO e il triangolo
mistilineo EDO ( regione piana limitata dall’arco DE di Γ e dagli assi cartesiani)
S2
di e del trapezio DCBO
Area di
Area di S1 =
Area di S2 =
Soluzione di Adriana Lanza
ovvero










