Università di Siena, DIISM, CdS in Ingegneria. Prova scritta di Fisica 2.
Siena 17 settembre 2015.
Risolvere gli esercizi seguenti e riportare nelle tabelle i risultati richiesti. Nella correzione dell’elaborato saranno valutati i
procedimenti che portano ai risultati in tabella. Asserzioni e calcoli vanno sinteticamente ma esplicitamente giustificati, poiché le
descrizioni dei procedimenti seguiti costituiscono un essenziale oggetto di valutazione.
Esercizio 1
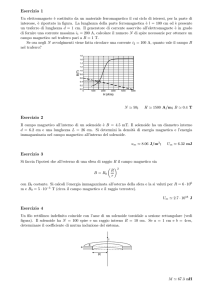
Si ha una carica Q uniformemente distribuita sulla superficie di un
disco forato. Il raggio del disco è 2R ed il raggio del foro è R.
z
z
Calcolare il potenziale elettrostatico sull’asse z dell'anello, in
funzione della distanza z dal piano del disco studiandone massimi,
minimi e comportamenti asintotici. Due quarti diametralmente
opposti di questa distribuzione vengono eliminati, determinare nelle
sue componenti il campo elettrostatico sull'asse z.
Esercizio 2
Si hanno due avvolgimenti solenoidali coassiali di forma cilindrica,
rispettivamente di raggio A e 2A, molto lunghi rispetto al loro diametro.
Ciascuno di essi è costituito da N spire di filo conduttore (sia ρ la sua
resistività) avente raggio a<<A. Si assuma che, su ciascun
avvolgimento, tali spire siano disposte in strato singolo, ciascuna a
contatto (meccanico, non elettrico!) con le sue adiacenti. Si assuma che i
due avvolgimenti siano collegati in serie, in modo che essi siano
percorsi da corrente nello stesso verso, per effetto di una f.e.m. ε0
applicata agli estremi liberi del filo.
Calcolare il campo magnetico generato dentro il cilindro interno e la potenza dissipata per effetto
Joule in un tratto lungo h del solenoide interno.
Esercizio 3
Si consideri il doppio solenoide dell’esercizio precedente con i due avvolgimenti percorsi da una
corrente I. Si immagini che una carica puntiforme Q di massa M transiti sull’asse con velocità V.
Stabilire per quali valori dell’angolo fra V e l’asse del solenoide la carica non uscirà dalla superficie
laterale del solenoide interno.
Esercizio 4
Si consideri il doppio solenoide degli esercizi precedente. I due avvolgimenti siano ora
elettricamente separati. Il solenoide esterno è percorso da una corrente dipendente dal tempo
secondo la legge I(t)=I0cos(ωt). Il solenoide interno sia chiuso su una resistenza R pari a 1000 volte
la resistenza di tutto il filo dei due avvolgimenti. Qual è la potenza media che viene dissipata sulla
resistenza R?
E’ ammesso trascurare gli effetti di autoinduzione, però si chiede di spiegare le ragioni che possono
consentire questa semplificazione.
Università di Siena, DIISM, CdS in Ingegneria. Prova scritta di Fisica 2.
cognome
nome
Siena 17 settembre 2015.
matricola
Tabella riassuntiva dei risultati
Esercizio 1
V(z)
Massimi/minimi
Comp. asintotico
Ex
Ey
Ez
V(z)
E(z)
Esercizio 2
B
P
Esercizio 3
θ
Esercizio 4
<P>
Spazio riservato alla commissione
Descrizione procedimenti: Ñ No (⇒compito insufficiente)
Es 1
« No ¼ ½ ¾ Ok
Es 2
« No ¼ ½ ¾ Ok
ѽ
Es 3
« No ¼ ½ ¾ Ok
Ñ Ok
Es 4
« No ¼ ½ ¾ Ok