TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
prof. Gianmarco de Felice, arch. Lorena Sguerri
PREDIMENSIONAMENTO E ANALISI DEI
CARICHI DEL SOLAIO
Norme per il predimensionamento
Analisi dei carichi permanenti
Sovraccarichi variabili
Combinazioni di carico
Esempio numerico / SAP 2000
Diagrammi di inviluppo
Correzioni sui diagrammi di inviluppo
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
B
L3
L4
L5
3.50
L2
L1
0.00
A
7.00
A
B
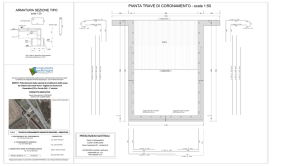
Sezione B-B:
sezione sul telaio di spina
7.00
Sezione A-A:
sezione sul solaio
3.50
0.00
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Predimensionamento dei solai
La Normativa Italiana e più precisamente il D.M. del
09/01/1996 – paragrafo 7, regola il progetto dei solai in
cemento armato prevedendo, sostanzialemente tre
categorie diverse:
Solai a getto pieno
Solai misti in c.a. e c.a.p. con elementi di alleggerimento
Solai con elementi prefabbricati in c.a. e c.a.p.
Per quanto riguarda la nostra esercitazione, bisogna progettare
un solaio appartenente alla seconda categoria e cioè un solaio
misto in cemento armato con elementi di alleggerimento in
laterizio.
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Predimensionamento di un solaio in c.a.
5.00
4.00
6.00
1.80
Dato uno schema strutturale come quello
rappresentato in figura è necessario
procedere con il predimensionamento del
solaio in base alla luce più grande.
5.00
Sezione trasversale schematica di un
generico solaio misto in latero-cemento.
armatura
superiore
La normativa (D.M.
09/01/96, par.7) fornisce
precise indicazioni sul suo
predimensionamento
armatura
inferiore
soletta collaborante
s
pignatta
h
travetto
bo
bp
i
bo
H
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Predimensionamento di un solaio in c.a.
D.M. 09/01/96, paragrafo 7
L è la luce della campata più lunga.
Considerando che una pignatta non è alta meno
di 12 cm, l’altezza minima del solaio è 16 cm.
In genere non si usano solette con spessore
maggiore di 5 cm., ma 4 cm è lo spessore più
usuale.
Altezza solaio
H ≥ 1/25 L
H ≥ 12 cm
Altezza soletta
s ≥ 4 cm
Interasse
travetto
i ≤ 15 s
Un interasse usuale è i = 50÷52 cm. a seconda
di bo, considerando una pignatta larga 40 cm.
bo ≥ 1/8 i
bo ≥ 8 cm
Dimensioni usuali sono bo = 10÷12 cm,
possibilmente non più di 14 cm; la larghezza
del travetto viene determinata anche in
funzione delle sollecitazioni di taglio previste.
bp ≤ 52 cm
In genere l’altezza delle pignatte è sempre un
numero pari: 12 ÷ 14 ÷ 16 cm ecc. Il minimo è
12 cm.
Larghezza
travetto
Dimensioni
pignatta
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Predimensionamento di un solaio in c.a.: esempio
Lmax = 5.00 m
s = 4 cm
⇒ H = 500 cm / 25 = 20 cm
⇒
h = 16 cm
Con s = 4 cm, H deve essere sempre un numero pari arrotondato per eccesso.
Per quanto riguarda la larghezza del travetto possiamo assumere che
se
se
Lmax > 6.00 m
Lmax < 6.00 m
Se si pone bp = 40 cm, si ottiene:
1.80
6.00
b0 = 12 cm
b0 = 10 cm
i = 50 ÷ 52 cm ≤ 15s = 60 cm
b0 = 10 cm
i = 50 cm
b0 = 10 cm > 50 cm / 8 = 6.25 cm
5.00
Nel caso specifico, si pone
5.00
4.00
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Predimensionamento di un solaio in c.a.: esempio
Lmax = 5.00 m
s = 4 cm
⇒ H = 500 cm / 25 = 20 cm
⇒
h = 16 cm
Con s = 4 cm, H deve essere sempre un numero pari arrotondato per eccesso.
Per quanto riguarda la larghezza del travetto possiamo assumere che
b0 = 12 cm
b0 = 10 cm
se
se
Lmax > 6.00 m
Lmax < 6.00 m
Se si pone bp = 40 cm, si ottiene:
armatura
superiore
i = 50 ÷ 52 cm ≤ 15s = 60 cm
Nel caso specifico, si pone
b0 = 10 cm
i = 50 cm
b0 = 10 cm > 50 cm / 8 = 6.25 cm
armatura
inferiore
soletta collaborante
s
pignatta
h
travetto
bo
bp
i
bo
H
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.
1.00
5.00
6.00
Il modello “trave continua” del solaio consente di individuare lo
stato di sollecitazione dei travetti sotto i carichi permanenti e
variabili assegnati.
1.80
5.00
4.00
Per comodità, ai fini dell’analisi dei carichi,
si può considerare che la trave continua
corrisponda ad una fascia di solaio larga 1 m.
Una volta predimensionato il solaio, bisogna
calcolare l’entità dei:
Carichi permanenti: peso del solaio, dei
materiali di finitura, dei tramezzi e di
eventuali altri elementi gravanti su di esso in
maniera permanente (ex. parapetti)
Carichi variabili: a seconda della
destinazione d’uso dell’edificio e del solaio
A
B
C
1.80
5.00
4.00
stesso (locali interni, copertura, balconi ecc.)
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.: esempio
Bisogna, in genere fare una distinzione tra solai con diverse destinazioni
d’uso che si differenziano per l’entità dei carichi accidentali, per materiali
di finitura e anche per dimensioni.
Nell’ambito dell’esercitazione, possono essere individuate tre tipologie
diverse:
Solai interpiano interni all’edificio
Solai interpiano di balconi o terrazze
Solai di copertura
Nel caso riportato nell’esempio, devono essere calcolati i carichi relativi
ad un solaio interpiano con balcone (sbalzo)
A
1.80
B
5.00
C
4.00
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.
SOLAIO INTERPIANO – INTERNO ALL’EDIFICIO
Destinazione d’uso:
Civile Abitazione
pavimento in ceramica
massetto
Dimensioni
4 cm
4 cm
16 cm
10 cm
40 cm
50 cm
100 cm
10 cm
intonaco
H = 20 cm
20 cm
s = 4 cm
i = 50 cm
bo = 10 cm
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.
SOLAIO INTERPIANO – BALCONE
⇒ Hb = H – 4 cm = 16 cm
L’altezza del solaio, in genere, viene ridotta di circa 4 cm per evitare
problemi di ingresso delle acque all’interno dell’edificio.
ATTENZIONE: l’altezza di un solaio non può essere inferiore a 16 cm. In
caso, si rinuncia a ridurre H incrementando, semmai, l’altezza del massetto
del solaio interno usando una malta di argilla espansa (12 kN/mc).
Particolare attenzione
pavimento in ceramica
massetto
impermeabilizzazione
bisogna porla, inoltre,
4 cm
quando si ha una
4 cm
12 cm
16 cm
terrazza molto ampia
poichè deve essere
intonaco
sempre rispettata la
10 cm
40 cm
10 cm
50 cm
norma H ≥ Lter/25
100 cm
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.
pavimento in ceramica
massetto
4 cm
4 cm
16 cm
10 cm
40 cm
10 cm
intonaco
50 cm
20 cm
Analisi dei carichi permanenti del solaio
interpiano: valori caratteristici relativi ad una
fascia di solaio larga 1 metro
100 cm
Materiale
h (m)
L (m)
Travetti (cemento armato)
0.16
0.1 x 2 25
0.8
Soletta (cemento armato)
0.04
1
1
Pignatte (laterizio)
0.16
0.4 x 2 5.5
0.7
Massetto (malta bastarda)
0.04
1
0.76
Pavimento (ceramica)
Intonaco
Tramezzi
TOTALE
(0.015)
P (kN/mc)
P (kN/mq)
25
19
P (kN/m)
1
0.4
0.4
1
0.3
0.3
1
1
1
4.96
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
Incidenza dei tramezzi
Sulla Circolare del 04/07/1996 n. 156 viene specificato che:
“Per gli orizzontamenti degli edifici per abitazioni e uffici, il carico
costituito da tramezzi di peso minore di 1.5 kN/mq potrà essere ragguagliato
ad un carico uniformemente
distribuito sul solaio pari a 1,5
volte il peso complessivo della
tramezzatura, semprechè vengano
adottate le misure costruttive atte
ad assicurare una adeguata
distribuzione del carico”
Il solaio in esame garantisce una
ripartizione adeguata del carico,
quindi è possibile adottare un
carico medio pari a 0.8÷1.2 kN/mq
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
pavimento in ceramica
massetto
impermeabilizzazione
4 cm
4 cm
12 cm
10 cm
40 cm
10 cm
16 cm
intonaco
50 cm
Analisi dei carichi permanenti del solaio
interpiano – balcone: valori caratteristici
relativi ad una fascia di solaio larga 1 m.
100 cm
Materiale
h (m)
L (m)
P (kN/mc)
Travetti (cemento armato)
0.12
0.1 x 2
25
0.6
Soletta (cemento armato)
0.04
1
25
1
Pignatte (laterizio)
0.12
0.4 x 2
5.5
0.53
Massetto (malta bastarda)
0.04
1
19
0.76
Pavimento (ceramica)
Intonaco
Impermeabilizzazione
TOTALE
(0.015)
P (kN/mq)
P (kN/m)
1
0.4
0.4
1
0.3
0.3
1
0.3
0.3
3.89
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
lastra di marmo
23
15
3
impermeabilizzazione
intonaco
100
Analisi dei carichi permanenti del solaio
interpiano – parapetto del balcone a sbalzo:
valore caratteristico relativo al parapetto
del balcone che deve essere calcolato come
un carico concentrato permanente da
applicare all’estremità libera della mensola
Materiale
h (m)
L (m)
S (m)
P (kN/mc)
Muratura piena
1
1
0.15
18
Lastra di marmo
(0.03)
1
0.23
0.8
0.18
Intonaco
1
1
(0.015)
0.3
0.3
Impermeabilizzazione
1
1
0.3
0.3
1
0.4
3.48
TOTALE
P (kN/mq)
P (kN)
2.70
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
SOLAIO DI COPERTURA:
L’analisi dei carichi di un solaio di copertura non differisce
sostanzialmente da quella riportata nell’esempio, ma bisogna tenere
presente che:
Il solaio non presenta dislivelli strutturali, quindi l’altezza H è sempre
quella di calcolo.
E’ da prevedere un manto d’impermeabilizzazione ovunque.
E’ necessario tenere conto del peso di parapetti o cornicioni solo alle
estremità libere delle mensole (se presenti).
Non vi sono tramezzi.
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
valori caratteristici dei sovraccarichi variabili
I valori caratteristici dei sovraccarichi variabili , a seconda delle diverse
destinazioni d’uso, sono indicati sulla Circolare del 04/07/1996 n. 156,
paragrafo 5.2.
In tabella sono riportati i valori utili ai fini dell’esercitazione
Destinazione d’uso
Qk
Civile abitazione e relativi terrazzi a livello
praticabili
2.00 kN/mq
Uffici aperti al pubblico e relativi terrazzi a
livello praticabili
3.00 kN/mq
Balconi e ballatoi
4.00 kN/mq
Copertura praticabile (terrazza)
A seconda della
destinazione d’uso
Copertura non praticabile
0.50 kN/mq
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
valori caratteristici dei sovraccarichi variabili
Nel caso di copertura o di terrazza, bisogna tenere conto anche del carico
neve.
Esempio:
Lazio (Zona II), as < 200 m ⇒ qsk = 1.15 kN/mq (carico neve al suolo)
Copertura piana
⇒
µ = 0.8 ⇒ qs = µ qsk = 0.8*1.15 = 0.92 kN/mq
La Circolare del 04/07/1996 n. 156, paragrafo 5.2. afferma chiaramente che
il sovraccarico dovuto alla neve non deve essere cumulato, sulle medesime
superfici con gli altri sovraccarichi variabili.
Di conseguenza, dato il sovraccarico variabile della copertura (praticabile o
meno), e dato il sovraccarico dovuto alla neve, tra i due si scelga quello più
gravoso.
Qk = max {Qvar ; qs}
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi dei carichi per un solaio in c.a.:
Tornando all’esempio, in tabella sono riportati i valori caratteristici e di
calcolo dei carichi permanenti e dei sovraccarichi variabili, agenti sul solaio
interpiano:
Pd = 1.4 x Pk Qk
Qd = 1.5 x Qk
Destinazione
d’uso
Pk
Solaio interno:
civile abitazione
4.96 kN/m 7.00 kN/m
2.00 kN/m 3.00 kN/m
Balcone
3.89 kN/m 5.50 kN/m
4.00 kN/m 6.00 kN/m
Parapetto
3.48 kN
4.90 kN
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Combinazioni di carico
Solaio a due campate con mensola (balcone): combinazioni di carico
e diagrammi dei momenti flettenti.
1° cdc
Fd
Q d1
Pd2
Pd1
A
B
C
A
B
Fd
Q d2
Q d1
Pd1
A
B
C
A
B
C
A
B
C
3° cdc
Fd
Q d1
Pd2
Pd1
A
B
C
4° cdc
Q d2
Fd
Q d1
Pd2
Pd1
A
B
C
A
B
B
C
A
B
C
C
2° cdc
Pd2
A
C
Diagramma di
inviluppo finale: sul
quale viene eseguito il
progetto delle
armature a flessione
Un diagramma
analogo può essere
ottenuto per la
sollecitazione di taglio
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Analisi delle sollecitazioni
Una volta preparato il modello e le combinazioni di carico si può passare
all’analisi delle sollecitazioni attraverso l’equazione dei Tre Momenti e
controllare i risultati tramite il SAP2000
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Verifica dei risultati
E’ importante non dare per scontato che i diagrammi delle sollecitazioni
forniti dal SAP2000 siano sicuramente esatti, poiché siamo noi ad inserire i
dati e il modello e questa operazione non è esente da errori.
Fd
D
Q d1
Pd2
MA
Pd1
A
B
C
D
A
MB
B
T"A
C
TD
T"B
A
T'A
B
T'B
T'C
Verificare che i diagrammi di taglio e momento siano congruenti con il
modello trave continua.
Verificare che i diagrammi di taglio e momento siano congruenti con i
carichi applicati. Ad esempio controllare che:
Æ (TA” + TB’)/LAB = (Pd1+ Qd1), ecc…
(in valori assoluti)
Æ TD = Fd
(in valori assoluti)
Æ MA = + Fd x LDA + Pd2 x L2DA/2
(in valori assoluti)
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Correzioni sul diagramma di inviluppo del Taglio
Per quanto riguarda gli appoggi intermedi, è possibile ridurre i valori della
sollecitazione di taglio e di conseguenza anche quella dei momenti negativi.
La generica trave su cui poggia il solaio, infatti, nella realtà non è un
appoggio puntiforme. Di conseguenza, la sua reazione non è concentrata in
corrispondenza dell’asse del vincolo, ma può essere ipotizzata come
uniformemente ripartita attorno ad esso per tutta la sua
larghezza. Come valore massimo del taglio, quindi, può
essere assunto
quello a filo della
trave e la sua
A
B
C
variazione, lungo
la larghezza
effettiva del
vincolo, sarà di
A
B
C
tipo lineare.
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Correzioni sul diagramma di inviluppo dei Momenti
La correzione effettuata sul diagramma del taglio consente di ridurre anche
il valore del massimo momento negativo in corrispondenza dell’appoggio.
La variazione lineare del taglio lungo la larghezza effettiva della trave
comporta una variazione parabolica del momento che non riesce a
raggiungere il suo valore di picco, ma un valore intermedio tra quello di
picco e quello a filo trave.
Æ Se la trave è emergente si può calcolare il momento in asse all’appoggio
come:
M’d
Msx
Md
Mdx
M’d = [max (Msx; Mdx) + Md]/2
Æ Se la trave è a spessore, in virtù della
sua maggiore deformabilità trasversale, si
può calcolare il momento in asse
all’appoggio come se si trattasse di una
trave emergente e quindi con base ridotta.
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Correzioni sul diagramma di inviluppo dei Momenti
La cerniera di estremità della trave continua, a momento nullo, rappresenta
nella realtà un vincolo di semincastro il cui momento è tutt’altro che nullo.
Per questo motivo, si
-(P +Q ) x L /24
aggiunge fuori calcolo
un momento negativo
C
che può essere calcolato
A
B
considerando la campata
Q d1 /2 come una trave
Pd1 /2 incastrata e caricata con
la metà del carico
B
C
complessivo
LBC
(permanente + variabile)
d1
MT
d1
2
BC
2
-[(Pd1+Qd1)/2] x LBC /12
B
C
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Correzioni sul diagramma di inviluppo dei Momenti
Per quanto riguarda l’esempio, il valore del momento negativo “aggiunto”
in corrispondenza della cerniera C sarà:
MC = -(Pd1+Qd1) · L2BC/24 = -(7.00 + 3) · 42/24 = -6.70 kN·m
Per tracciare il tratto di diagramma che interessa si può ricorrere alla legge
di variazione del momento per la trave incastrata con carico uniformemente
distribuito pari a (Pd1+Qd1)/2
27.45 kN m
21.20 kN m
6.70 kN m
A
13.11 kN m
B
13.84 kN m
0.85
C
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Correzioni sul diagramma di inviluppo dei Momenti
M(x) = MC + [(Pd1+Qd1) · LBC /4] · x - [(Pd1+Qd1)/2] · x2/2
Inserendo i valori noti e risolvendo l’equazione di 2° grado in x, si ottiene
l’ascissa in corrispondenza della quale il momento flettente si annulla:
M(x) = -6.70 + [(7+3) · 4 /4] · x - [(7+3)/2] · x2/2
M(x) = -6.70 + 10 · x – 2.5 · x2
3.148 m
⇒
x=
0.852 m
2
-[(Pd1+Qd1)/2] x LBC /12
B
C
3.148
0.852
0.852
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE
Diagrammi di inviluppo di Taglio e Momento corretti
A
B
C
A
B
C
E’ importante tenere ben presente che i diagrammi inviluppo sono relativi
ad una striscia di solaio larga un metro comprendente due travetti. Per avere
i valori delle sollecitazioni relative ad un solo travetto, bisogna moltiplicare
i diagrammi per l’interasse tra i travetti stessi.