Universita' di Trento <[email protected]>
Meccanica Applicata alle Macchine
Compito 27/2/03
I modulo: punti 1 e 2 - Esame completo: punti 1 e 3.
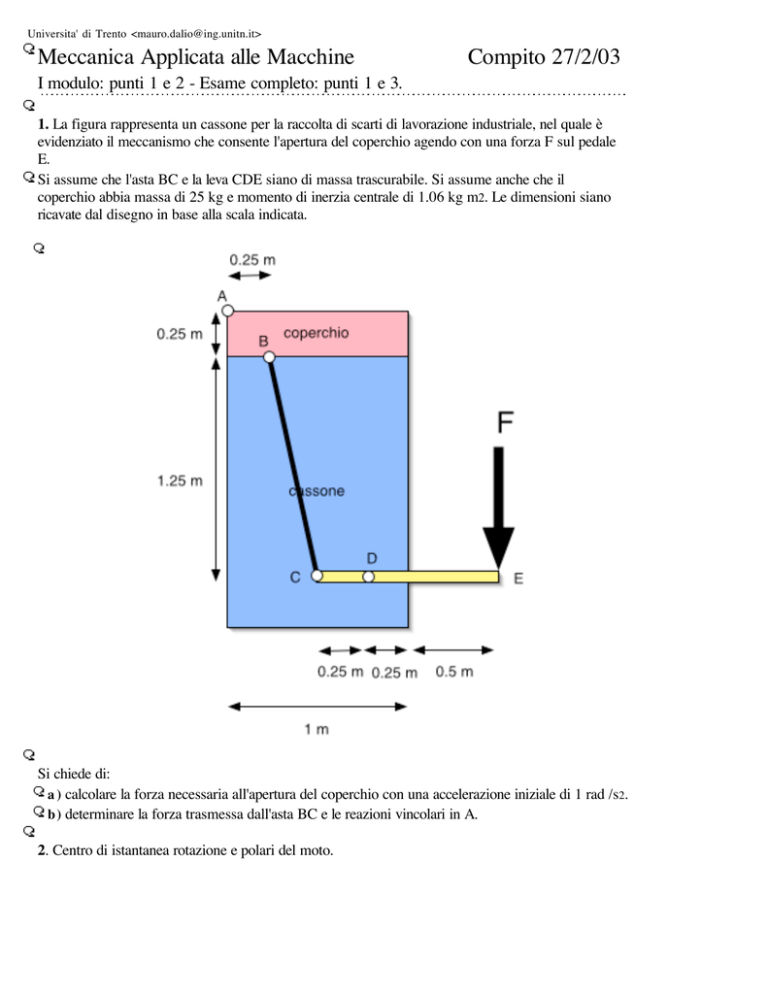
1. La figura rappresenta un cassone per la raccolta di scarti di lavorazione industriale, nel quale è
evidenziato il meccanismo che consente l'apertura del coperchio agendo con una forza F sul pedale
E.
Si assume che l'asta BC e la leva CDE siano di massa trascurabile. Si assume anche che il
coperchio abbia massa di 25 kg e momento di inerzia centrale di 1.06 kg m2. Le dimensioni siano
ricavate dal disegno in base alla scala indicata.
Si chiede di:
a ) calcolare la forza necessaria all'apertura del coperchio con una accelerazione iniziale di 1 rad /s2.
b ) determinare la forza trasmessa dall'asta BC e le reazioni vincolari in A.
2. Centro di istantanea rotazione e polari del moto.
Universita' di Trento <[email protected]>
3. Si consideri un modello di antenna per telecomunicazioni come in figura. Le 3 masse m=50 kg
rappresentano la massa della struttura concentrata ad intervalli di un terzo della altezza totale (che è
di 25 m). Ciascun segmento è modellato come una struttura elestiche di rigidezza k=100.000.000 N
/m.
Determinare modi di vibrare e frequenze naturalidella struttura.
Universita' di Trento <[email protected]>
SOLUZIONE ESERCIZIO 3
Dati: m = 50
k = 100 106
Equazioni del moto:
∂
∂t
∂
∂t
∂
∂t
m 0 0
0 m 0
0 0 m
∂
y
∂t 1
∂
y
∂t 2
∂
y
∂t 3
+
2k - k 0
- k 2k - k
0 -k k
y1
y2
y3
=0
E' un'equazione differenziale a coefficienti costanti, per cui la soluzione é del tipo:
y1
y2
y3
=
Y1
Y2
Y3
ew it
sostituendo si ottiene:
- w
m 0 0
0 m 0
0 0 m
2
+
2k - k 0
- k 2k - k
0 -k k
Y1
Y2
Y3
e
w it
eq. (1)
=0
Affinché il sistema abbia soluzione il determinante deve essere uguale a zero:
- w
2
m 0 0
0 m 0
0 0 m
+
2k - k 0
- k 2k - k
0 -k k
=0
polinomio caratteristico
- k2 k - w 2 m + 2k - w 2 m k - w 2 m 2k - w 2 m - k2 = 0
- 125000 w 2 - 3.9612¥105 w 2 - 3.1099¥106 w 2 - 6.494¥106 = 0
Le soluzioni sono gli autovalori
Prima pulsazione naturale
w 2 = 3.9612¥105
Sostituendo in eq. 1 si ottiene l'autovalore
Normalizzando
Y 12 + Y 22 + Y 32 = 1
9.2959 a 2 = 1
Y1 = a
Y 3 = 2.247 a
Y 2 = 1.8019 a
a = 0.32799
Y 1 = 0.32799
Y 2 = 0.59101
Y 3 = 0.73698
Universita' di Trento <[email protected]>
w 2 = 3.1099¥106
seconda pulsazione naturale
Normalizzando
Y 12 + Y 22 + Y 32 = 1
Y1 = a
Y 2 = 0.44504 a
Y 3 = - 0.80194 a
a = 0.73698
Y 1 = 0.73698
Y 2 = 0.32799
Y 3 = - 0.59101
terza pulsazione naturale w 2 = 6.494¥106
Sostituendo in eq. 1 si ottiene l'autovalore
Normalizzando
Y 12 + Y 22 + Y 32 = 1
Y1 = a
Y 3 = 0.55496 a
Y 2 = - 1.247 a
a = 0.59101
Y 1 = 0.59101
Y 3 = 0.32799
Y 2 = - 0.73698
Universita' di Trento <[email protected]>
Universita' di Trento <[email protected]>
SOLUZIONE ESERCIZIO 1
Per la risoluzione dell'esercizio sono possibili due strade: l'utilizzo del Principio dei Lavori Virtuali
per il calcolo della forza F. Tuttavia l'esercizio richiede anche le forze dell'asta e della cerniera A per
cui si deve applicare l'approccio di Newton-Eulero. Quindi é preferibile usare tale approccio per
risolvere l'esercizio completo.
Si applica l'approccio di Newton-Eulero ai 3 corpi.
Il sistema di riferimento utilizzato é quello indicato in figura.
ASTA
E' noto che applicando le equazioni di Newton Eulero
ad un asta senza massa, con due cerniere agli estremi,
si ottiene che la reazione é lungo la retta che unisce
le due cerniere (come indicato in figura).
l'angolo a é l'angolo della configurazione iniziale dell'asta
come indicato in figura.
Le equazioni sono le seguenti
a = arctan 1.25
0.25
T x = T cos a
T
x
=
1
26
26 T
a = arctan 5
T
y
= T sin a
T
y
=
1
26
eq.(1)
650 T
PEDALE
Il pedale é schematizzato come un'asta senza
massa.
In D si ha una cerniera che vincola il pedale al
telaio.
In figura sono indicate le reazioni e forze
esterne e la reazione
dell'asta BC.
Le equazioni sono:
0 = RD x - T
x
equilibrio alla traslazione lungo x
Universita' di Trento
<[email protected]>
equilibrio alla traslazione lungo x
= RD
- Tx
x
0 = RD y + T
0= T
y
y
- F
equilibrio alla traslazione lungo y
0.25 + F 0.75
equilibrio alla rotazione (polo in D)
usando eq.(1) dalla terza equazione si ottiene:
eq.(2)
T = - 0.12 650 F
COPERCHIO
Il coperchio é l'unico corpo con massa.
In figura sono indicate le forze agenti sul coperchio.
Va notato che pur essendo il coperchio fermo (la sua
velocità iniziale di traslazione e rotazione sono nulle),
é soggetto ad un'accelerazione di rotazione che causa
anche un'accelerazione iniziale del baricentro.
Le equazioni sono:
eq.(3) equilibrio alla traslazione lungo x
∂ ∂ xG = RA + T
x
x
∂t∂t
eq.(4) equilibrio alla traslazione lungo y
m ∂ ∂ yG = RA y - T y - m g
∂t∂t
eq.(5) equilibrio alla rotazione (Polo A)
I A ∂ ∂ q = T x 0.25 - 0.25 T y - m g 0.5
∂t∂t
dove, nella configurazione iniziale:
AG = 0.51539
AG = 0.52 + 0.25 2
m
2
I
A
= 1.06 + m AG 2
b = arctan
0.25
2
I
A
= 7.7006
b = arctan 0.25
m = 25
g = 9.81
q = 2p - b
0.5
Calcolo accelerazione baricentro:
Posizione: xG = AG cos q
yG = AG cos q
Velocità:
∂ xG = ∂ AG cos q
∂ yG = ∂ AG sin q
∂t
∂t
∂t
∂t
Accelerazione:
∂ ∂ xG = ∂ ∂ AG cos q
∂ ∂ yG = ∂ ∂ AG sin q
∂t ∂t
∂t ∂t
∂t ∂t
∂t ∂t
Impoendo le condizioni iniziali:
∂ q =0
∂ ∂ q =1
∂ ∂ xG = AG sin b
∂ ∂ yG = AG cos b
∂t
∂t∂t
∂t∂t
∂t∂t
Combinando le equazioni 1-5 si ottiene:
RA x = 133.45
RA y = - 393.88
F = 217.21
E sostituendo a ritroso si ottengono:
Universita' di Trento <[email protected]>
E sostituendo a ritroso si ottengono:
T = - 664.53
RD x = - 130.33
RD
y
= 868.84