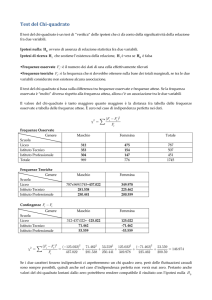
RELAZIONE TRA VARIABILI DAL PUNTO DI VISTA DESCRITTIVO E INFERENZIALE
Date 2 variabili X e Y, categoriali, ordinali o cardinali ricondotte in classi, possiamo rappresentarne
la distribuzione di frequenza congiunta in una tabella a doppia entrata detta tabella di contingenza
Obiettivo: conoscere come si distribuiscono i casi sulla variabile x, all’interno di ciascuna modalità
della variabile y.
Frequenze marginali:
L’ultima riga e l’ultima colonna rappresentano rispettivamente la distribuzione di frequenza
(univariata) marginale di colonna e di riga
Frequenze congiunte:
le celle interne della tabella riportano la distribuzione di frequenza (bivariata) congiunta delle 2
variabili.
Per calcolare il valore della cella generica nij la formula è la seguente:
ni * nj
nij = -------N
Rappresentazione grafica bivariata per variabili caridnali
=> diagramma di dispersione
È un diagramma cartesiano nel quale i punti rappresentano i casi e le variabili costituiscono gli assi,
in esso è del tutto assente l’informazione sulla distribuzione congiunta.
Le coordinate di ogni punto del diagramma non sono altro che i valori che il caso presenta sulle
due variabili
Scopo di una tabella di contingenza è mettere in evidenza l’eventuale relazione tra due variabili
categoriali
Indipendenza e indipendenza in media
Se due eventi sono indipendenti, la probabilità condizionale è data da:
P(A|B)=P(A)
E la probabilità congiunta di due eventi sarà:
P(AeB)=P(B)*P(A|B)=P(B)*P(A)
Si ha indipendenza tra le variabili se ciascuna distribuzione parziale è uguale alla corrispondente
distribuzione marginale.
Formalmente: Y|x1= Y|x2=Y
Calcolo delle frequenze attese nel caso di indipendenza tra le 2 variabili
A partire dai marginali di riga e colonna possiamo calcolare le frequenza di cella che dovremmo
aspettarci di trovare nel caso di completa indipendenza tra le due variabili.
Partendo dalle frequenze assolute, possiamo calcolare ciascuna frequenza teorica facendo il
prodotto dei relativi marginali e dividendo il risultato per il totale del collettivo.
Formula per calcolare gli attesi
Calcolando tutte le frequenze attese, otteniamo la tabella delle frequenze teoriche
La tabella delle frequenze teoriche riporta le frequenze in caso di indipendenza tra le 2 variabili.
Più la tabella delle frequenze empiriche si discosta da quella teorica, più elevato è il grado di
associazione fra le 2 variabili.
L’operatore chi2si basa sulla differenza tra le frequenze empiriche e teoriche
Esempio
Quale distribuzione teorica bisogna utilizzare per fare inferenza sul test del chi2?
-> La variabile aleatoria χ2
Si dice variabile aleatoria χ2 con n gradi di libertà una funzione di variabili aleatorie, data dalla
somma dei quadrati di n variabili aleatorie indipendenti, normali standardizzate.
La v. a. chi2 si distribuisce secondo una funzione di densità che ha una forma che dipende dai gradi
di libertà (n).
Il valore teorico del chi2 per diversi gdl, è riportato nelle tavole
Inferenza sul chi2: test di ipotesi
Per valutare la probabilità di ottenere un determinato valore di chi2 per effetto del caso,
utilizziamo la distribuzione di probabilità teorica del chi2 nota e tabulata.
Si tratta di una famiglia di distribuzioni che dipende dal numero di gradi di libertà della tabella.
I gdl in una tabella di contingenza sono il numero di celle libere di variare una volta fissati i
marginali della tabella.
Come si calcolano?
Per una tabella di contingenza rxc, il numero di gdl sarà dato da numero di righe (r) meno 1 per il
numero di colonne (c) meno 1, ovvero dalla formula:
Gdl=(r-1)(c-1)
Nel nostro esempio i gdl sono: (2-1)(2-1)=1
Costruiamo il sistema di ipotesi:
H0: tra consumo di droghe e rendimento scolastico non c’è
associazione
H1: tra consumo di droghe e rendimento scolastico esiste una
Associazione
a=0.01
Calcoliamo la statistica test sui dati del campione con la formula:
Cerchiamo sulle tavole il valore di chi teorico (critico) per a=0.01 e gdl=1: c2
critico,1,a=0.01=6.635
Facciamo inferenza: Il valore da noi ottenuto 13.09 è maggiore del chi2 teorico=6.635, quindi
rifiutiamo l’ipotesi nulla e concludiamo dicendo che il consumo di droghe è significativamente
associato con il rendimento scolastico
Quando abbiamo tabelle 2x2 possiamo utilizzare la formula abbreviata che ci permette di calcolare
il chi2 a partire dalle frequenze di cella e marginali, senza calcolare gli attesi:
considerazioni rispetto alla variabile aleatoria chi2:
la statistica chi2 si distribuisce come la variabile aleatoria chi2 in modo approssimatico (tanto
migliore tanto più il campione è ampio).
Non è però possibile definire una numerosità del campione precisa, dal momento che vi sono
diversi totali da prendere in considerazione.
Come regola generale possiamo dire che più i*j è grande più il campione deve essere numeroso.
Se nella tabella di contingenza vi sono delle celle vuote la statistica non si distribuisce come una
chi2. dipende anche da come si distribuiscono le singole variabili.
deve essere adeguata al numero di celle e a come si distribuiscono le variabili
empiricamente: vanno guardate le frequenze teoriche ( ) minori di 5, se sono più del 20%
non è possibile calcolare il chi2. [soluzioni possibili: cambiare il tipo di test o accorpare le
categorie)
NB: PER TUTTI I TEST DI VERIFICA DI IPOTESI:
effettuato un test e trovata una significatività statistica, questo non vuol dire che la relazione
trovata sia forte, dipende da quanto ci allontaniamo dal valore atteso.
Quando un test richiede degli assunti per poter essere fatto è detto test parametrico (ad esempio
nel test per la differenza tra media abbiamo assunto che il fenomeno si distribuisca normalmente).
Il chi2 non richiede alcun assunto, è un test non parametrico (distribution free)
Quando possibile è sempre meglio utilizzare un test parametrico, è più capace di rifiutare ipotesi
nulle false, di ridurre 1-β. Questa capacità è dettapotenza di un test
I test parametrici sono più potenti dei test non parametrici.
Chi2 e fi sono operatori di connessione=> statistiche che quantificano solo l’intensità di una
relazione, quanto ci si allontana da una condizione di indipendenza.
Questo tipo di relazione assumerà sempre valori positivi, mai negativi.
Lo 0 è assunto quando c’è indipendenza tra le variabili.
Il chi2 può essere calcolato per qualunque tipo di variabile (anche cardinale con raggruppamento
in classi), ma così vengono perse molte informazioni
MISURE DI CONCORDANZA/DISCORDANZA
Misure per variabili cardinali
Forniscono informazioni, oltre che sull’intensità, anche sulla direzione della variazione di una
variabile al variare dell’altra.
Si caratterizzano per la presenza di un punto neutro, lo zero, (assenza di concordanza) e due poli,
uno positivo (concordanza) e uno negativo (discordanza).
POSSONO ASSUMERE VALORI SIA POSITIVI CHE NEGATIVI
> 0 = concordanza (relazione positiva)
< 0 = discordanza
(relazione negativa)
= 0 indipendenza assoluta oppure indipendenza lineare.
La concordanza con variabili categoriali si può calcolare se:
1.le variabili X e Y sono dotate dello stesso numero di modalità, e
2.ogni modalità di X è affine ad una e solo una modalità di Y, e viceversa.
Come si misura l’associazione tra due variabili cardinali? Covarianza = misura assoluta
formula abbreviata: media di x*y sottratto a x medio*y medio
anche la covarianza (come la varianza) è un momento centrale di II ordine
la varianza è un momento omogeneo, la covarianza è un momento misto
test di verifica di ipotesi (relativo al coefficiente di correlazione lineare)
è un test parametrico => assunti sulla popolazione :
distribuzione delle proprietà nella popolazione : normale bivariata (utilizzo variabili aleatorie
multidimensionali)
La distribuzione si comporta come una normale bivariata (distribuzione di densità di probabilità
congiunta)
Funzione di densità di probabilità camgiunta
sono i parametri che governano la funzione (media e varianza di x e y)
-> “rho” controparte a livello della popolazione del coefficiente di correlazione (rxy)
se Rho è uguale a 0 => la funzione dipende solo da μ e σ delle due varaibili
rappresentazione grafica: su tre dimensioni
si presenta come un cappello, l’area totale che sta sotto il cappello è uguale a 1
TEST DEL CHI2 PER LA BONTA’ DI ADATTAMENTO
Si può usare il test del chi2 anche su una singola distribuzione
Avendo solo una varaibile => gdl = n° della modalità della variabile –1
K DI COHEN
Il K di Cohen fornisce una misura del grado di accordo tra i due giudici, al di là del grado di
concordanza tra i giudizi che ci si aspetterebbe per caso.
Si considerano soltanto le frequenze poste sulla diagonale principale, quelle cioè che riguardano
l’incrocio tra le categorie affini.
Il K di Cohen si calcola come:
θ = Accordo osservato
Accordo residuo non casuale =
K = 1: perfetto accordo tra i due giudici
K=:
= perfetto disaccordo
K = 0: completa indipendenza tra i giudizi
Accordo atteso