specchio concavo

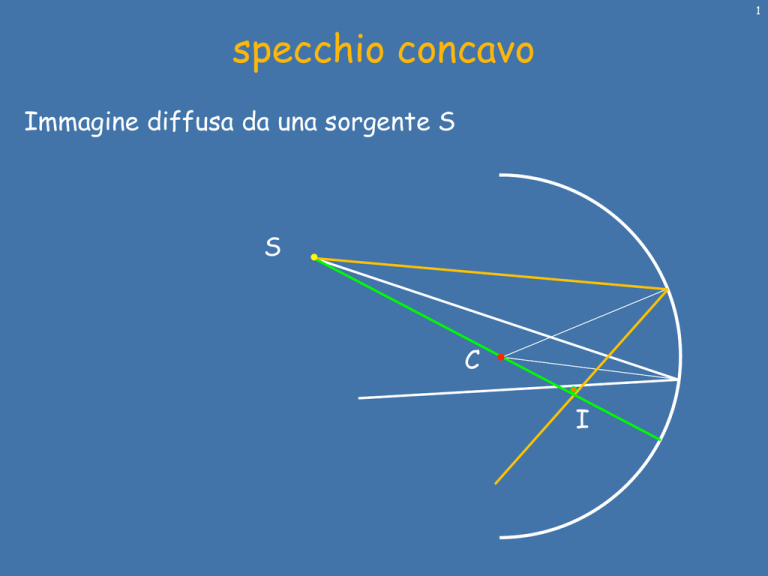
1
specchio concavo
Immagine diffusa da una sorgente S
S
C
I
2
specchio concavo
immagine I della sorgente S
S
C
I
3
propagazione delle onde
principio di Huygens
S
4
interferenza
sovrapposizione di onde
il risultato, nel punto in cui avviene la sovrapposizione, è
n l’annullamento
n il rafforzamento
n una situazione intermedia fra i due estremi
5
interferenza
sovrapposizione di onde
6
interferenza
per osservare l’interferenza occorre che questa sia
stabilmente presente
7
interferenza
La radiazione incidente passa attraverso le fenditure A e B
e nel punto P le onde arrivano in concordanza di fase.
A
x1
B
x2
onda A: EA = E0 cos(ωt+kx1)
onda B: EB = E0 cos(ωt+kx2)
P
8
interferenza
Concordanza di fase implica che
ωt+kx1 = ωt+kx2 + 2π·n
da cui (k = 2π/λ)
x1 - x2 = 2π·n/k = n λ
Nel punto P le onde si sommano e il campo elettrico è la
somma dei due singoli campi
9
interferenza
AC = n λ
AC = AB sen ϑ = d sen ϑ
A
C
d
B
ϑ
x1
ϑ
x2
interferenza costruttiva
d sen ϑ = n λ
P
10
interferenza
La radiazione incidente passa attraverso le fenditure A e B
e nel punto P le onde arrivano in discordanza di fase.
Le due onde si elidono a vicenda
A
x1
B
onda A: EA = E0 cos(ωt+kx1)
onda B: EB = E0 cos(ωt+kx2)
x2
P
11
interferenza
Discordanza di fase implica che
ωt+kx1 = ωt+kx2 + 2π·(n - 1/2)
da cui (k = 2π/λ)
x1 - x2 = 2π·(n - 1/2)/k = (n - 1/2) λ
Nel punto P le onde si sommano e il campo elettrico è nullo
12
interferenza
AC = (n - 1/2) λ
AC = AB sen ϑ = d sen ϑ
A
d
C
ϑ
x1
ϑ
B
x2
interferenza distruttiva
d sen ϑ = (n - 1/2) λ
P
13
interferenza
due fenditure, distanti d = 10 λ.
Massimi per sen ϑ = n λ/d
Minimi per sen ϑ = (n - 1/2) λ/d
interferenza
0,00
0,05
n=1
1,00
intensità
angolo (rad)
0,10
0,15
0,20
0,25
n=2
0,80
0,60
0,40
0,20
0,00
0
n=1
5
n = 210
angolo (°)
15
14
interferenza
10 fenditure, distanti d = 10λ. Massimi per sin ϑ = n λ/d
interferenza
0,00
angolo (rad)
0,10
0,15
0,05
0,20
0,25
intensità
1,00
0,80
0,60
0,40
0,20
0,00
0
5
10
angolo (°)
15
15
interferenza
interferenza con ondoscopio
16
diffrazione
La radiazione incidente si diffonde oltre la fenditura di
larghezza D e arriva nel punto P.
Dal punto intermedio H discordanza di fase con B
A
H
xA
B
xB
P
17
diffrazione
Da A e B concordanza di fase:
ωt+kxA = ωt+kxB + 2π·n
da cui (k = 2π/λ)
xA - xB = 2π·n/k = n λ
Nel punto P le onde si elidono a coppie e il campo elettrico è
nullo
18
diffrazione
AC = n λ
AC = AB sen ϑ = D sen ϑ
A
B
C
ϑ
xA
ϑ
xB
interferenza distruttiva
D sen ϑ = n λ
P
19
per n = 1
diffrazione
D sen ϑ = λ da cui ϑ = λ/D
questo valore di ϑ rappresenta la posizione angolare del
primo minimo
A
B
C
ϑ
xA
ϑ
xB
interferenza distruttiva
D sen ϑ = λ
P
20
diffrazione
AC = 3/2 λ
HB = 2/3 AB
AC = AB sen ϑ = D sen ϑ
energia solo da regione fra A e H
regione fra H e B produce interferenza distruttiva
A
C
H
B
ϑ
ϑ
xA
xB
interferenza costruttiva
D sen ϑ = 3/2 λ
P
21
diffrazione
AC = 5/2 λ
HB = 4/5 AB
AC = AB sen ϑ = D sen ϑ energia solo da regione fra A e H
regione fra H e B produce interferenza distruttiva
A
C
H
B
ϑ
xA
ϑ
xB
interferenza costruttiva
D sen ϑ = 5/2 λ
P
22
diffrazione
in generale AC = (n + 1/2) λ
HB = AC n/(n + 1/2)
regione fra H e B produce interferenza distruttiva
energia solo da regione fra A e H
A
C
H
B
ϑ
xA
ϑ
xB
interferenza costruttiva
D sen ϑ = (n + 1/2) λ
P
23
diffrazione
1 fenditura, larghezza D = 20 λ. Minimi per sen ϑ = n λ/D
diffrazione
angolo (rad)
0,00
0,05
0,10
0,15
0,20
0,25
intensità
1,00
n = 1
0,80
n = 2
0,60
0,40
0,20
0,00
0
5
10
angolo (°)
15
24
diffrazione
onde del mare
25
diffrazione
porto di Fiumicino
26
potere risolutivo
criterio di Rayleigh
27
potere risolutivo
criterio di Rayleigh – fari auto
http://online.scuola.zanichelli.it/cutnellelementi-files/pdf/InterferenzaLuce_Cutnell_Zanichelli.pdf
28
potere risolutivo
minima distanza risolubile
potere risolutivo
0,61 λ
d=
n senα
1 R=
d
α
29
potere risolutivo
nel caso di strumenti ottici α ≈ 90°, in aria n = 1
0,61 λ 0,61·550·10-9
d=
=
≈ 0,3µ m
n senα
1
per l’occhio in aria α ≈ 1/250
d occhio
0,61 λ 0,61·550·10-9
=
=
≈ 0,1 mm
n senα
1 / 250
30
reticolo di diffrazione
2 fenditure, distanti d = 20λ. Massimi a sin ϑ = n λ/d
interferenza modulata dalla diffrazione
angolo (rad)
0,00
0,10
0,20
intensità
1,00
0,80
0,60
0,40
0,20
0,00
0
5
10
angolo (°)
15
31
reticolo di diffrazione
20 fenditure, distanti d = 20λ. Massimi a sin ϑ = n λ/d
interferenza modulata dalla diffrazione
angolo (rad)
0,00
0,10
0,20
intensità
1,00
0,80
0,60
0,40
0,20
0,00
0
5
10
angolo (°)
15
32
reticolo di diffrazione
due lunghezze d’onda λ1 e λ2, ∆λ = 0,1
10 fenditure, distanti d = 20 λ1. Massimi a sin ϑ = n λ1 /d
interferenza modulata dalla diffrazione
angolo (rad)
0,00
0,05
0,10
0,15
0,20
intensità
1,0
0,8
0,6
0,4
0,2
0,0
0
2
4
6
8
angolo (°)
10
12
14
33
reticolo di diffrazione
due lunghezze d’onda λ1 e λ2, ∆λ = 0,1
50 fenditure, distanti d = 20 λ1. Massimi a sin ϑ = n λ1 /d
interferenza modulata dalla diffrazione
angolo (rad)
0,00
0,05
0,10
0,15
0,20
intensità
1,0
0,8
0,6
0,4
0,2
0,0
0
2
4
6
8
angolo (°)
10
12
14
34
reticolo di diffrazione
due lunghezze d’onda λ1 e λ2, ∆λ = 0,01
100 fenditure, distanti d = 20 λ1. Massimi a sin ϑ = n λ1 /d
interferenza modulata dalla diffrazione
angolo (rad)
0,00
0,05
0,10
0,15
0,20
intensità
1,0
0,8
0,6
0,4
0,2
0,0
0
2
4
6
8
angolo (°)
10
12
14
35
reticolo di diffrazione
nel caso in cui ripetessimo lo stesso esperimento con oggetti
pesanti - palline di ferro od altro - si otterrebbe una
immagine dello schermo
36
reticolo di diffrazione
se eseguito con particelle atomiche - tipo elettroni - si
ottiene una figura di interferenza.
La figura di interferenza si
ottiene anche se si opera
con un elettrone alla volta.
37
reticolo di diffrazione
ipotesi di De Broglie
alcune analogie della meccanica classica, il comportamento
duale della r.e.m. lo portarono all’ipotesi
E hf h
=
per un’onda p = =
c c λ
anche per una particella
E hf h
p= =
=
c c λ
da cui
h h
λ= =
p mv
38
reticolo di diffrazione
questa relazione è anche in accordo con il modello di Bohr
della struttura dell’atomo
Gli elettroni stanno su particolari orbite dove non perdono
energia. Queste orbite sono definite dall’avere un momento
angolare
nh
mvr =
2π
Se ogni elettrone è associato ad un’onda, la sua orbita è
stabile se contiene un numero intero di lunghezze d’onda
2πr = nλ
––>
e quindi
nmvλ nh
mvr =
=
2π
2π
nλ
r=
2π
39
reticolo di diffrazione
pacchetto d’onda come somma di onde elementari
40
reticolo di diffrazione
molecole di ftalocialina attraverso un opportuno reticolo
per la visualizzazione, la
singola molecola è stata
eccitata con un laser e
la luce emessa rivelata
da una camera EMCCD.
Questa tecnologia ha
permesso di determinare
il punto di impatto della
molecola entro 10 nm.
Markus Arndt and Thomas Juffmann - Vienna Center for Quantum Science and Technology
effetto fotoelettrico
probabilità dell’evento ≈ Z 5 / E3,5
γ
e-
effetto Compton
probabilità dell’evento ≈ Z / E
γ’
ϑ
γ
ϕ
hf' =
hf
1+
hf
(1 -cosϑ )
m 0c
λ aumenta e l’energia diminuisce
e-
effetto coppia
e+
probabilità dell’evento ≈ Z 2
E ≥ 1,022 MeV = 2 m0c2
γ
ϕ
ϕ
e-
radiazioni γ nella materia
radiazioni γ in acqua
intensità della radiazione γ
1.25
1 MeV
1
100 keV
0.75
10 keV
0.5
0.25
0
0
5
10
15
20
profondità (cm)
25
30
radiazioni α nella materia
particelle α in acqua - Eα = 6 MeV
perdita d’energia per unità di percorso
dE/dx
200
150
100
50
0
0
0.01
0.02
0.03
0.04
percorso (mm)
0.05
0.06