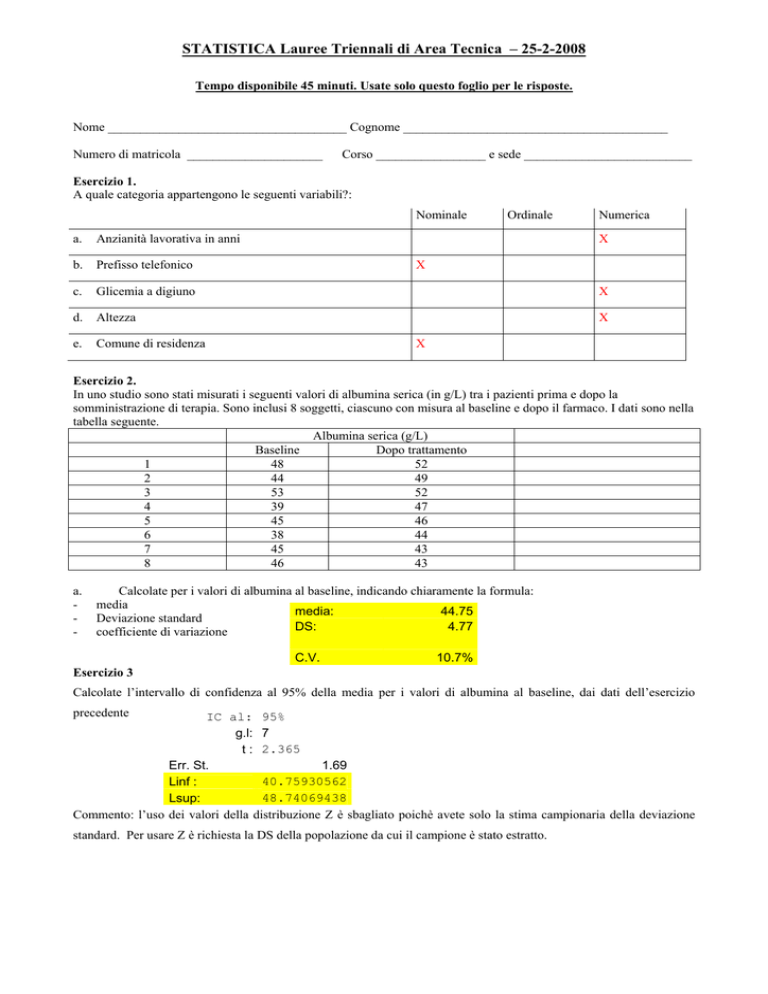
STATISTICA Lauree Triennali di Area Tecnica – 25-2-2008
Tempo disponibile 45 minuti. Usate solo questo foglio per le risposte.
Nome _____________________________________ Cognome _________________________________________
Numero di matricola _____________________
Corso _________________ e sede __________________________
Esercizio 1.
A quale categoria appartengono le seguenti variabili?:
Nominale
Ordinale
Numerica
a.
Anzianità lavorativa in anni
X
b.
Prefisso telefonico
c.
Glicemia a digiuno
X
d.
Altezza
X
e.
Comune di residenza
X
X
Esercizio 2.
In uno studio sono stati misurati i seguenti valori di albumina serica (in g/L) tra i pazienti prima e dopo la
somministrazione di terapia. Sono inclusi 8 soggetti, ciascuno con misura al baseline e dopo il farmaco. I dati sono nella
tabella seguente.
Albumina serica (g/L)
Baseline
Dopo trattamento
1
48
52
2
44
49
3
53
52
4
39
47
5
45
46
6
38
44
7
45
43
8
46
43
a.
-
Calcolate per i valori di albumina al baseline, indicando chiaramente la formula:
media
media:
44.75
Deviazione standard
DS:
4.77
coefficiente di variazione
C.V.
10.7%
Esercizio 3
Calcolate l’intervallo di confidenza al 95% della media per i valori di albumina al baseline, dai dati dell’esercizio
precedente
IC al: 95%
g.l: 7
t : 2.365
Err. St.
1.69
40.75930562
Linf :
48.74069438
Lsup:
Commento: l’uso dei valori della distribuzione Z è sbagliato poichè avete solo la stima campionaria della deviazione
standard. Per usare Z è richiesta la DS della popolazione da cui il campione è stato estratto.
Esercizio 4
Con riferimento ai dati dell’esercizio 2, calcolate il test statistico appropriato per valutare l’ipotesi nulla (Ho): “il
farmaco non modifica la concentrazione di albumina”.
a)
Quale test avete scelto? T Student per dati appaiati
Spiegate perchè il test scelto è applicabile ai dati ed al problema posto; I dati sono coppie di osservazioni appaiate;
non dispongo di informazioni sulla popolazione e quindi debbo stimare DS dal campione; la distribuzione della
differenza tra due variabili spesso corrisponde a una distribuzione normale.
b) Scrivete la formula;
c)
t=
d −0
s
n
Eseguite i calcoli;
diff.
4
5
-1
8
1
6
-2
-3
media:
DS:
Err. St.
t:
scarto quadratico delle differenze
3.0625
7.5625
10.5625
33.0625
1.5625
14.0625
18.0625
27.5625
2.25
4.062019
1.436141
1.566699
d) Calcolate il valore della probabilità che i due gruppi siano un’estrazione casuale dalla stessa popolazione, secondo
le tabelle allegate.___p > 0,10 (valore esatto è p=0,16)__
Esercizio 5.
In un'indagine epidemiologica sono state campionate 100 persone, che sono state classificate secondo i seguenti
caratteri: A = episodi influenzali durante l'inverno, B = uso dei mezzi pubblici, ottenendo la seguente tabella:
Episodi influenzali durante l’inverno
Totale
Nessuno
Uno o più di uno
Usa abitualmente mezzi pubblici
16
50
66
Non usa mezzi pubblici
22
12
34
Totale
38
62
100
a.
Quale indicatore di associazione calcolate l’Odds Ratio. Scrivete la formula ed il risultato
Commento: le colonne sono state scambiate rispetto alla posizione abituale, per verificare l’attenzione con cui le tabelle
dei dati vengono lette. Sono quindi possibili due strategie di soluzione:
Soluzione consigliata: riordino della tabella nel modo abituale e calcolo dell’OR di episodi influenzali per chi usa mezzi
pubblici rispetto a chi non li usa.
I risultati diventano: OR= (50*22) / (16*12) = 5.73
episodi
influenzali
uno o più
OR=
5.72917
nessuno
mezzi si
50
16
66
mezzi no
Totale
12
62
22
38
34
100
IC al: 95%
ln(or)=
es(ln(OR)
li(ln(OR)
ls(ln(or))
1.74557
0.45966
0.84465
2.64649
z : 1.960
Linf (OR): 2.3271674
Lsup(OR): 14.104422
Soluzione sconsigliata (ma ammessa): mantenimento della tabella calcolo dell’OR di NON avere episodi influenzali per
chi usa mezzi pubblici rispetto a chi non li usa.
I risultati diventano: OR= (16*12) / (50*22) =0,175
episodi
influenzali
nessuno
OR=
uno o più
0.17455
IC al: 95%
mezzi si
16
50
66
mezzi no
Totale
22
38
12
62
34
100
ln(or)=
-1.7456
es(ln(OR) 0.45966
li(ln(OR) -2.6465
ls(ln(or)) -0.8447
Il calcolo di chi quadrato non varia e quindi viene presentato solo per la soluzione consigliata:
b.
z : 1.960
Qual è il numero di gradi di libertà appropriato per questi dati? _______1____________
Linf (OR): 0.0708998
Lsup(OR): 0.4297069
c.
(oss −att )
χ =∑
2
Calcolate la statistica Chi Quadrato, scrivendo la formula:
2
att
attesi
mezzi si
mezzi no
nessuno
uno o più
25.080
40.920
12.920
21.080
38
62
66
34
100
contributo a calcolo chi^2
Con corr. Yates (non
Senza corr. Yates
richiesta
3.287
2.015
2.935
1.799
6.381
3.911
5.698
3.492
chi2=
prob <
d.
15.595
0.0001
chi2=
prob <
13.924
0.0002
In generale, quale informazione viene fornita dalla statistica Odds Ratio?
OR fornisce una stima del rischio di sviluppare un effetto quando è presente un fattore antecedente rispetto al
corrispondente rischio quando il fattore è assente
e.
In generale, quale informazione viene fornita dalla statistica Chi Quadrato?
Il test statistico misura la probabilità di osservare una tabella come quella data (o più estrema) se vale l'ipotesi nulla.
f.
Come interpretate il valore di Chi Quadrato che avete ottenuto?. (Avete fissato l’errore di 1° tipo al 5%. ). Usate in
proposito le tavole allegate
chi2=
prob <
g.
15.595
0.0001
Come interpretate il valore di Odds Ratio che avete ottenuto?
Nel caso di modifica della tabella l’interpretazione è: Chi usa MP ha un rischio di contrarre episodi influenzali 5,72
volte maggiore rispetto a chi non usa MP.
Nel caso di uso tabella senza variazione delle colonne l’interpretazione è: Chi usa MP ha un rischio di NON contrarre
episodi influenzali pari a 0,17 volte quello di chi non MP. Si noti che 0,174 = 1/5,73
____________________________________________________________________________________________
h
Calcolate l’intervallo di confidenza al 95% dell’Odds Ratio
I risultati sono indicati nelle risposte alla domanda A.
Distribuzione T
1 coda
Probabilità
gradi libertà ↓
2 code
0,005
0,010
0,025
0,050
0,010
0,020
0,050
0,100
1
63,66
31,82
12,71
6,31
63,66
31,82
12,71
6,31
2
9,22
6,96
4,30
2,92
9,22
6,96
4,30
2,92
3
5,84
4,54
3,18
2,35
5,84
4,54
3,18
2,35
4
4,60
3,75
2,78
2,13
4,60
3,75
2,78
2,13
5
4,03
3,37
2,57
2,02
4,03
3,37
2,57
2,02
6
3,71
3,14
2,45
1,94
3,71
3,14
2,45
1,94
7
3,50
3,00
2,37
1,90
3,50
3,00
2,37
1,90
8
3,36
2,90
2,31
1,86
3,36
2,90
2,31
1,86
9
3,25
2,82
2,26
1,83
3,25
2,82
2,26
1,83
10
3,17
2,76
2,23
1,81
3,17
2,76
2,23
1,81
11
3,11
2,72
2,20
1,80
3,11
2,72
2,20
1,80
12
3,06
2,68
2,18
1,78
3,06
2,68
2,18
1,78
13
3,02
2,65
2,16
1,77
3,02
2,65
2,16
1,77
14
2,98
2,63
2,15
1,76
2,98
2,63
2,15
1,76
15
2,95
2,60
2,13
1,75
2,95
2,60
2,13
1,75
16
2,92
2,58
2,12
1,74
2,92
2,58
2,12
1,74
17
2,90
2,57
2,11
1,73
2,90
2,57
2,11
1,73
18
2,88
2,55
2,10
1,73
2,88
2,55
2,10
1,73
19
2,86
2,54
2,09
1,73
2,86
2,54
2,09
1,73
20
2,85
2,53
2,09
1,73
2,85
2,53
2,09
1,73
per numeri di g.l. superiori a 20 usate la riga corrispondente a 20
Distribuzione Chi quadrato
Probabilità
gradi libertà
0,001
0,01
0,025
0,05
0,1
1
10,83
6,64
5,02
3,84
2,71
2
13,82
9,21
7,38
5,99
4,61
3
16,27
11,35
9,35
7,82
6,25
4
18,47
13,28
11,14
9,49
7,78
5
20,52
15,09
12,83
11,07
9,24
6
22,46
16,81
14,45
12,59
10,65
7
24,32
18,48
16,01
14,07
12,02
8
26,13
20,09
17,54
15,51
13,36
9
27,88
21,67
19,02
16,92
14,68
10
29,59
23,21
20,48
18,31
15,99
11
31,26
24,73
21,92
19,68
17,28
12
32,91
26,22
23,34
21,03
18,55
13
34,53
27,69
24,74
22,36
19,81
14
36,12
29,14
26,12
23,69
21,06
15
37,70
30,58
27,49
25,00
22,31
16
39,25
32,00
28,85
26,30
23,54
17
40,79
33,41
30,19
27,59
24,77
18
42,31
34,81
31,53
28,87
25,99
19
43,82
36,19
32,85
30,14
27,20
20
45,32
37,57
34,17
31,41
28,41
per numeri di g.l. superiori a 20 usate la riga corrispondente a 20
Distribuzione normale standard
1 coda
Probabilità
2 code
0,001
0,01
0,025
0,05
0,1
0,001
0,01
0,02
0,05
0,1
3,09
2,33
1,96
1,65
1,29
3,30
2,58
2,33
1,96
1,65