Campo elettrico
F
1 q
E= =
q0 4 πε0 r 2
€
Unità di misura = N/C
Domanda
Tutte le cariche in figura hanno lo stesso valore assoluto. In
quale delle configurazioni il campo elettrico nel punto P è
massimo?
1- A
2- B
3- C
4- D
5- non si può determinare
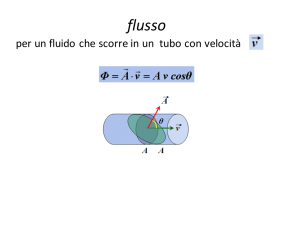
Flusso
Φ = v ⋅ nˆ A = (v cos θ ) A
€
Flusso del campo elettrico
Φ = ∑ E ⋅ nˆ dΣ
€
dΦ = E ⋅ nˆ dΣ = EdΣ 0 cos θ
Φ=
€
∫ E ⋅ nˆdΣ
€
€
€
€
Angolo solido
ds ds′
dθ = =
cosθ
r
r
dΣ dΣ′
dΩ = 2 = 2 cosθ
r
r
dΩ = sin θdθdϕ
π 2π
Ω=
∫ ∫ sinθdθdϕ = 2π [−cosθ ]
0
0
2π
0
= 4π
€
Legge di Gauss
ε0Φ = qint
ε0 ∫ E ⋅ nˆ dΣ = qint
€
Gauss = Coulomb
ε0 ∫ E ⋅ nˆ dΣ = qint
ε0 ∫ EdΣ =ε0 E ∫ dΣ =ε0 E 4 πr 2 = q
1 q
E=
4 πε0 r 2
Domanda
Una barretta cilindrica di materiale isolante è immersa in un
campo elettrico, come mostrato in figura. Il flusso netto del
campo elettrico che attraversa la superficie del cilindro è:
1- positivo
2- negativo
3- nullo
Piano di cariche
ε0 ∫ E ⋅ nˆ dΣ =qint
ε0 ( EA + EA) = σA
σ
E=
2ε0
€
Domanda
La carica elettrica per unità di area è +σ per la piastra 1 e –
σ per la piastra 2. Se le due piastre sono sistemate
affacciate l’una sull’altra come in figura, il campo elettrico
vale:
1- 2σ/ε0 tra le piastre, 0 al di fuori
2- σ/ε0 tra le piastre, 0 al di fuori
3- 0 tra le piastre e al di fuori
4- ±σ/ε0 tra le piastre e al di fuori
5- nessuna delle precedenti
Guscio sferico
1- Un guscio sferico carico
uniformemente non esercita
alcuna forza su una carica posta al
suo interno
ε0 ∫ E ⋅ nˆ dΣ =qint
ε0 ( E 4 πr ) = 0
2
€
2- Un guscio sferico carico
uniformemente attrae o respinge
una carica al di fuori del guscio
€
come se tutta la carica del guscio
fosse nel centro.
ε0 ∫ E ⋅ nˆ dΣ =qint
ε0 ( E 4 πr 2 ) = q
E =0 , r<R
1 q
E=
, r≥R
2
4 πε0 r
Sfera carica
1 q′
E=
, r ≤ R,
2
4 πε0 r
q′ carica racchiusa in una sfera di raggio r
q′
=
q
4 3 4 3
πr
πR
3
3
1 q
E =
r
3
4 πε0 R
€
⇒
r3
q′ = q 3
R
Linea di cariche
ε0 ∫ E ⋅ nˆ dΣ =qint
ε0 ( E2πrh ) = λh
λ
E=
2πε0 r
€
Problemi
1. Una sfera uniformemente carica avente raggio di 2 m ha una densità di
carica superficiale di 9.1 µC/m2. (a) Si trovi la carica totale della sfera. (b) Si
trovi il flusso elettrico totale uscente dalla sfera.
2. Il grafico in figura mostra l’intensità del campo elettrico in funzione della
distanza r dal centro di una sfera con una carica positiva uniforme distribuita
uniformemente su tutto il suo volume. Quanto vale la carica totale della sfera?