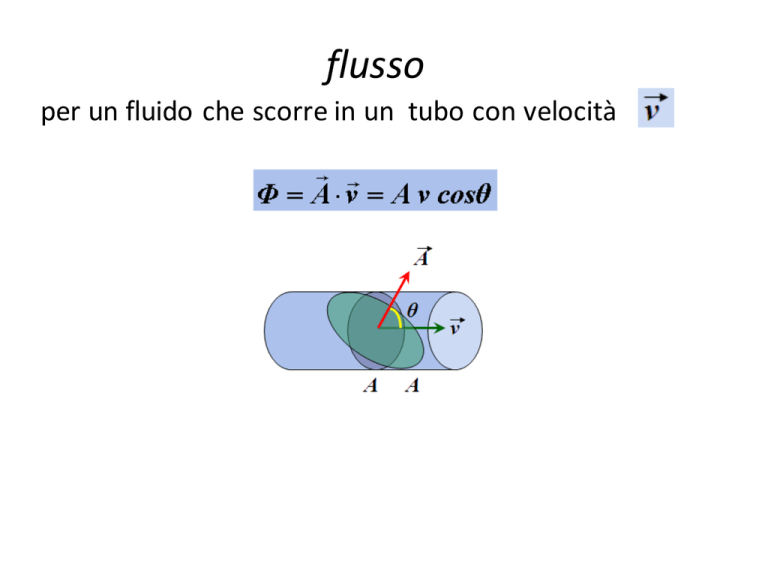
flusso
per un fluido che scorre in un tubo con velocità
flusso del campo elettrico attraverso una superficie di area A
numero di linee per unità di area
positivo se le linee escono, negativo se entrano
flusso del campo elettrico, superficie chiusa
E dA
integrale di superficie chiusa
il verso del vettore della superficie infinitesima è quello uscente. Con
questa definizione in 1 il flusso è entrante, in 2 è nullo e in 3 è uscente
carica positiva, sfera immaginaria
in ogni punto di S
teorema di Gauss
angolo solido
al centro della sfera
sotteso da
l’angolo solido è adimensionale, si misura in steradianti
angolo solido (totale) sotteso dalla sfera
in un piano l’angolo è il rapporto tra arco e raggio
l’angolo è adimensionale, si misura in radianti
angolo sotteso dalla
circonferenza
se la carica è esterna per ogni elemento di superficie elementare che è
sotteso da un angolo dΩ dalla carica puntiforme q, si può prolungare
l’angolo solido sino a intercettare un’altra superficie infinitesima dall’altro
lato dell’intera superficie. Per queste due superfici intercettate le
orientazioni delle normali sono tali che il flusso totale è nullo
teorema di Gauss
Il flusso del campo elettrico attraverso una superficie chiusa è
qint
ΦE
E dA
ε0
qint è la somma algebrica delle cariche interne alla superficie
La superficie chiusa attraverso cui si calcola il flusso è una
superficie geometrica, che non necessariamente coincide con una
superficie fisica
Il flusso del campo elettrico non dipende dalle posizioni delle
cariche all’interno della superficie, ma solo dalla loro somma
Il teorema di Gauss permette di calcolare il campo elettrico
generato da distribuzioni di cariche che presentano particolari
simmetrie
linee di campo e flusso
linee del campo elettrico generato da un dipolo (cariche puntiformi
+q , –q)
il flusso del campo elettrico attraverso
una superficie è proporzionale al
numero di linee di campo che la
attraversano ( positive le linee uscenti,
negative quelle entranti)
S1: qint>0, ФE>0: le linee di forza sono tutte uscenti
dalla superficie
S2: qint<0, ФE<0: le linee di forza sono tutte entranti
nella superficie
S3,S4: qint=0, ФE=0: per ogni linea di forza entrante
nella superficie ce n’è una uscente
filo infinito uniformemente carico, simmetria cilindrica
piano isolante uniformemente carico, simmetria cilindrica
Campo di un condensatore piano
Un condensatore piano ideale è formato da due lastre piane
(armature) parallele indefinite cariche con densità di carica
opposte +σ e –σ
+σ
–σ
σ
E1
E1
E1
E
1
E2
2ε0
σ
2ε0
E2
E=0
E2
E2
E
E=0
Il campo elettrico si calcola con il principio di sovrapposizione:
E
E1
E2
Nelle regioni esterne il campo elettrico è nullo, mentre in quella
interna esso è diretto dalla lastra positiva a quella negativa
E
σ
ε0
sfera uniformemente carica
Il campo è radiale per simmetria
assumiamo la sfera come superficie gaussiana
all’esterno: come se
tutta la carica fosse al
centro
sfera uniformememente carica
in sintesi :
l’andamento del modulo del campo prodotto da
una sfera uniformemente carica in funzione della
distanza radiale è lineare crescente all’ interno
della sfera e coulombiano all’ esterno della sfera
E
E
Q
4
0
r
a3
E
1 Q
4 0 r2
sfera non conduttrice uniformemente carica
conduttori
Campo del guscio sferico cavo di raggio a caricato con
carica totale Q uniformmente distribuita sulla
superficie
dobbiamo distinguere due casi :
r>a e r<a
all’esterno della distribuzione di
cariche, ossia per r > a
il calcolo procede esattamente
come nel caso della sfera carica
e il risultato e’
E
1 Q
4 0 r2
campo coulombiano come se tutta la carica Q fosse
concentrata nel centro della sfera
21
guscio sferico
( E) E 4 r 2
(E)
qint
0
E 0
0
come per la sfera uniformemente
carica
E
1 Q
4 0 r2
campo coulombiano
confronto sfera e guscio sferico
Potenziale del guscio sferico
all’esterno del guscio il potenziale è coulombiano
1 Q
V (r )
cost
4 0 r
il campo ha una discontinuità in r = a ma il potenziale deve essere continuo
ovunque
all’interno il campo E è nullo quindi il potenziale è costante all’interno, per
continuità assumiamo che all’interno il potenziale ha lo stesso valore che ha
sulla superficie
1 Q
V (r )
4 0 a
potenziale guscio sferico
due sfere conduttrici collegate












