Appunti di statistica medica

Appunti di statistica medica
AA 2016
Contents
TEOREMA DEL LIMITE CENTRALE ED ERRORE STANDARD . . . . . . . . . . . . . .
1
INTERVALLO DI CONFIDENZA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
IL TEST DI IPOTESI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
L’IPOTESI NULLA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
Un esempio: il test t di Student . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
Un esempio di test di ipotesi con dati nominali: il test del χ2 . . . . . . . . . . . . . .
9
Gli studi clinici . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
Gli studi osservazionali. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Gli studi sperimentali. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
L’interpretazione dei risultati . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
Le meta-analisi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
La piramide delle evidenze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
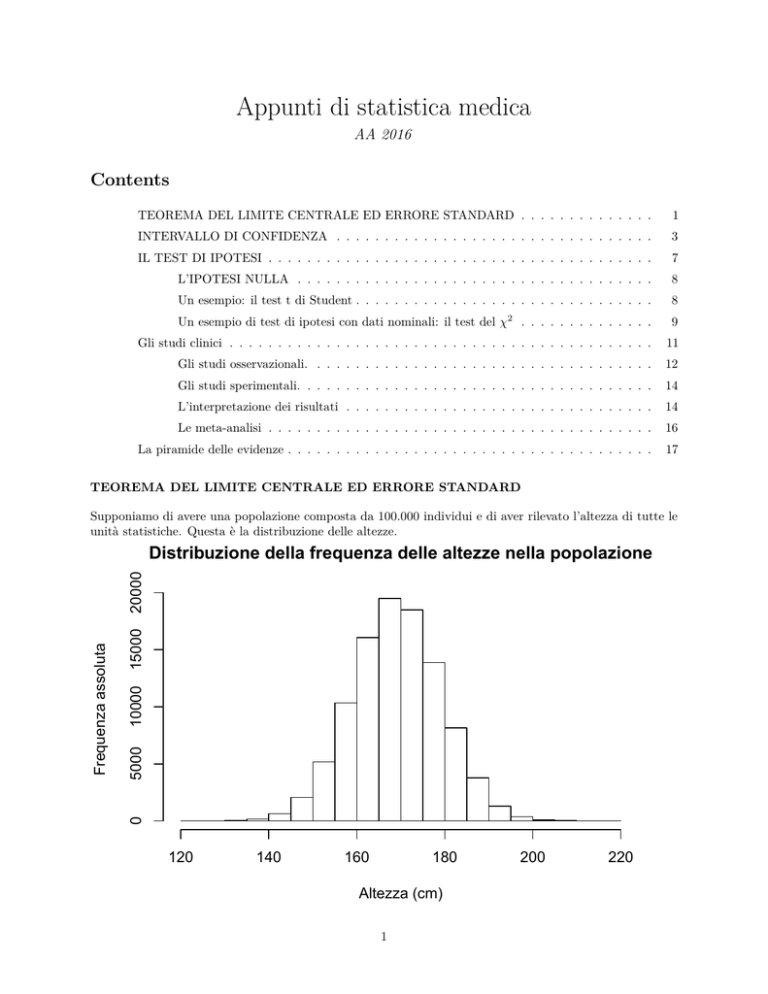
TEOREMA DEL LIMITE CENTRALE ED ERRORE STANDARD
Supponiamo di avere una popolazione composta da 100.000 individui e di aver rilevato l’altezza di tutte le
unità statistiche. Questa è la distribuzione delle altezze.
15000
10000
5000
0
Frequenza assoluta
20000
Distribuzione della frequenza delle altezze nella popolazione
120
140
160
180
Altezza (cm)
1
200
220
La media e la deviazione standard della popolazione sono 169±10 cm.
Estraiamo casualmente 100 campioni dalla popolazione, ciascuno composto da 16 unità, e raggruppiamo i
dati individuali in una tabella. Vediamo i primi 10 campioni ottenuti. In ogni riga ci sono i valori individuali
dei soggetti di ciascuno dei campioni.
##
##
##
##
##
##
##
##
##
##
##
1
2
3
4
5
6
7
8
9
10
1
181
171
166
185
171
175
171
171
160
187
2
173
163
170
160
159
162
166
189
171
146
3
160
143
162
180
165
167
154
157
181
153
4
162
156
158
177
168
182
167
171
166
178
5
169
169
169
144
180
154
162
180
165
176
6
171
159
155
165
178
167
169
183
180
169
7
176
180
160
179
169
172
159
186
170
181
8
161
175
173
173
163
182
180
168
172
164
9
168
185
181
161
180
175
160
174
172
164
10
164
154
172
168
188
174
176
164
167
175
11
154
157
164
155
181
158
179
170
172
161
12
162
175
180
171
163
169
191
165
161
176
13
158
172
162
171
177
189
176
156
158
171
14
179
151
189
162
167
173
183
157
169
171
15
171
174
169
186
173
170
163
166
152
183
16
160
161
169
156
174
174
159
171
163
178
Facciamo ora la media delle altezze in ciascun campione ed aggiungiamola come ultima colonna alla tabella.
##
##
##
##
##
##
##
##
##
##
##
1
2
3
4
5
6
7
8
9
10
1
181
171
166
185
171
175
171
171
160
187
2
173
163
170
160
159
162
166
189
171
146
3
160
143
162
180
165
167
154
157
181
153
4
162
156
158
177
168
182
167
171
166
178
5
169
169
169
144
180
154
162
180
165
176
6
171
159
155
165
178
167
169
183
180
169
7
176
180
160
179
169
172
159
186
170
181
8
161
175
173
173
163
182
180
168
172
164
9
168
185
181
161
180
175
160
174
172
164
10
164
154
172
168
188
174
176
164
167
175
11
154
157
164
155
181
158
179
170
172
161
12
162
175
180
171
163
169
191
165
161
176
13
158
172
162
171
177
189
176
156
158
171
14
179
151
189
162
167
173
183
157
169
171
15
171
174
169
186
173
170
163
166
152
183
16 media
160
167
161
165
169
169
156
168
174
172
174
171
159
170
171
170
163
167
178
171
Possiamo osservare che la media delle altezze nei primi 10 campioni è 169 cm (cioè ugualealla media della
popolazione) solo una volta, ma che comunque tutti i valori sono vicini alla media della popolazione. Per
avere una visione di insieme dei risultati vediamo la distribuzione di frequenza delle medie dei campioni.
2
0
5
10
15
Frequenza assoluta
20
Distribuzione della frequenza delle altezze della media dei campioni
160
165
170
175
180
Altezza (cm)
La media e la deviazione standard delle 100 medie campionarie (cioè dei campioni) è 169±2.5 cm: la media
delle medie campionarie tende quindi ad essere uguale alla media della popolazione, con una deviazione
standard campionaria è molto più stretta della deviazione standard della popolazione.
In linea generale possiamo affermare che con l’aumentare del numero di campioni, la media delle medie
campionarie tende a coincidere con quella della popolazione. Questa proprietà è definita “TEOREMA DEL
LIMITE CENTRALE”. La variabilità delle medie campionarie è invece nettamente ridotta rispetto alla
variabilità della popolazione. In altri termini gli individui della popolazione possono differire tra loro molto
di più di quanto possano essere diverse tra loro le medie di campioni estratti della medesima popolazione.
La variabilità delle medie della popolazione è espressa come deviazione standard. La variabilità
delle medie
√
campionarie è invece definita ERRORE STANDARD, che può essere calcolato come sd/ n, dove ‘sd’ è la
devizione standard della popolazione ed ‘n’ è il numero di soggetti inclusi in ciascun campione. Nel nostro
√
esempio, la deviazione standard della popolazione è 10, il numero di soggetti della popolazione 16. La 16 è
4, quindi ci possiamo aspettare un errore standard di 10/4=2.5. Esattamente quello che osserviamo con i
nostri dati. Con un numero sufficientemnte elevato di campioni (e/o con campioni sufficientemente grandi)
si potrà sempre avere la conferma sperimentale del TEOREMA DEL LIMITE CENTRALE e del calcolo
dell’errore standard (come è avvenuto nel nostro esempio).
INTERVALLO DI CONFIDENZA
Riprendiamo i dati sull’altezza delle popolazioni e ipotizziamo di ottenere 1000 campioni di 16 soggetti
ciascuno. La distribuzione delle medie campionarie è presentata nella figura.
##
##
##
##
##
##
1
2
3
4
5
1
174
160
184
174
191
2
165
161
166
147
161
3
172
155
161
157
168
4
168
173
176
152
171
5
163
181
184
156
175
6
171
172
182
181
155
7
154
164
176
171
176
8
178
172
190
164
173
9
180
164
183
173
165
10
160
177
195
164
181
3
11
170
170
175
173
176
12
180
169
178
143
155
13
161
151
152
173
177
14
159
154
154
165
172
15
173
169
163
171
149
16 media
181
169
167
166
183
175
170
165
144
168
##
##
##
##
##
6
7
8
9
10
161
163
173
170
184
165
169
172
174
175
163
173
177
177
187
177
193
169
169
167
182
166
185
173
164
155
170
194
182
174
190
199
178
145
171
156
180
161
156
178
163
175
187
169
175
175
183
162
167
184
161
164
143
181
187
153
176
162
165
169
158
164
165
185
161
169
158
171
175
174
164
156
172
182
154
159
173
160
162
159
166
173
171
171
173
0.10
0.00
0.05
Densità
0.15
Distribuzione della frequenza delle altezze della media dei campioni
160
165
170
175
Altezza (cm)
0.10
0.05
1.96 SD
1.96 SD
0.00
Densità
0.15
Distribuzione della frequenza delle altezze della media dei campioni
160
165
170
Altezza (cm)
4
175
180
Sull’asse verticale c’è la probabilità di ottenere una determinata media media campionaria. L’area sotto la
curva dipinta in blu è compresa tra la media meno 1.96 deviazioni standard dalla media (cioè 1.96 volte
l’errore standard ) e la media più 1.96 deviazioni standard dalla media. Lo strano numero “1.96” moltiplicato
per la deviazione standard ha una proprietà particolare nelle distribuzioni normali: il 95% delle osservazioni
sono comprese tra la media-1.96 · sd e la media + 1.96 · sd. Quando estraiamo un campione dalla popolazione,
pertanto possiamo aspettarci che nel 95% dei casi (cioè nel 95% dei possibili campioni) la vera media della
popolazione sia più vicina di 1.96 · sd dalla media del campione, in eccesso o in difetto. Possiamo pertanto
affermare che l’intervallo ottenuto da una media campionaria ± 1.96 · sd contenga la media della popolazione
nel 95% dei campioni di quella popolazione. Questo intervallo viene definito INTERVALLO DI CONFIDENZA
AL 95% perchè ci consente di avere fiducia (al 95%) di sapere l’intervallo in cui viene compresa la media della
popolazione, a noi sconosciuta. La deviazione standard utilizzata per l’intervallo di confidenza è quella della
popolazione delle medie campionarie, a noi sconosciuta allo stesso modo della media delle medie campionarie.
Si utilizza quindi un valore superiore a 1.96, che dipende dalla numerosità del campione, calcolato per le
distribuzioni t di Student.
5
6
IL TEST DI IPOTESI
I test di ipotesi sono probabilmente la modalità più frequente di statistica inferenziale. Esistono moltissimi
test diversi tra loro, ma tutti hanno in comune lo stesso ragionamento sottostante. Si fa una ipotesi teorica e
si verifica quanto possa essere probabile osservare i dati che abbiamo rilevato qualora l’ipotesi fosse vera. Ad
esempio potremmo fare l’ipotesi che l’altezza media di una popolazione sia 180 cm. Potremmo poi scegliere
un campione della popolazione e fare la media delle altezze delle unità del campione. Ipotizziamo che l’altezza
media campionaria sia 170 cm: nel test di ipotesi cerchiamo di calcolare la probabilità di ottenre un campione
con l’altezza media di 170 cm quando l’altezza media della popolazione è 180 cm. Questa probabilità si
espirme con la lettera p e può assumere un valore tra 0 (assolutamente impossibile ottenere questo campione
quando l’ipotesi iniziale è vera) a 1 (è certo che questo sia un campione della popolazione quando è vera
l’ipotesi iniziale).
Spesso il test di ipotesi ha come obiettivo il confronto di 2 o più campioni tra loro. Ad esempio potrei
misurare la pressione del sangue in soggetti ipertesi che assumono un placebo ed in soggetti che assumono un
farmaco anti-ipertensivo. Se la pressione rilevata fosse diversa nei due gruppi, dovrei concludere che il farmaco
anti-ipertensivo è efficace, viceversa dovrei abbandonare l’utilizzo di quel farmaco nella pratica clinica.
Ad esempio ipotizziamo di rilevare la pressione arteriosa diastolica in 20 pazienti che anno assunto il placebo
ed in 20 che hanno assunto il farmaco tutti i giorni nell’ultimo mese.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
media±sd
Placebo
Farmaco
96
98
107
108
99
116
97
102
112
93
99
103
87
111
88
116
101
88
84
93
100±10
95
90
90
96
89
88
90
93
82
76
91
97
101
85
99
82
88
98
92
103
91±7
Media e deviazione standard sono 100 ± 10 mmHg nel gruppo ‘Placebo’ e 91 ± 7 mmHg nel gruppo ‘Farmaco’.
E’ sufficiente questo per concludere che il farmaco è più efficace del placebo? Ricordiamo che stiamo studiando
il risultato su campioni. Se a noi interessa la risposta su questi particolari 40 pazienti, possiamo accontentarci
di valutare la differenza tra le medie. Ma se siamo interessati a generalizzare il risultato per tutti i pazienti
ipertesi, dobbiamo essere consapevoli che abbiamo rilevato dati da campioni per stimare l’effetto sulle
popopazioni. In realtà noi siamo interessati a sapere se la POPOLAZIONE dei pazienti che assume il
farmaco ha una pressione arteriosa diversa dalla POPOLAZIONE dei soggetti che assumono il placebo. I
prossimi pazienti a cui eventualmente somministreremo il farmaco antiipertensivo infatti faranno parte della
POPOLAZIONE dei pazienti ipertesi e non del campione che abbiamo già studiato.
7
L’IPOTESI NULLA
Per affrontare il confronto tra placebo e farmaco anti-ipertensivo con il test di ipotesi, dobbiamo prima di
tutto formulare una ipotesi e quindi verificare se i nostri dati sono con essa compatibili. La maggior parte
delle volte, l’ipotesi di partenza è una ipotesi di uguaglianza. In questo caso l’ipotesi iniziale quindi può
essere: la media della pressione diastolica della popolazione dei pazienti che assumo il placebo è uguale alla
media della pressione diastolica nei pazienti che assumo il farmaco. Questa ipotesi di uguaglianza è detta
IPOTESI NULLA ed indicata con H0 . Formalmente si può scrivere: H0 : µplac = µf arm , dove µ è la
media della popolazione.
Sappiamo che le medie dei nostri campioni sono probabilmente un po’ diverse dalle medie delle rispettive
popolazioni. Possiamo però calcolare la probabilità di ottenere proprio queste due medie campionarie quando
le medie delle due popolazioni sono uguali. Da considerare che due popolazioni con la stessa media (e la
stessa deviazione standard) per il carattere osservato sono da considerarsi un’unica popolazione. Per questo
motivo possiamo vedere il test ipotesi come la definizione della probabilità che i due campioni (nel nostro
esempio i soggetti che anno assunto il placebo e quelli che hanno assunto il farmaco) siano campioni casuali
estratti dalla stessa popolazione.
Un esempio: il test t di Student
Il test appropriato per il caso in esempio è il test t di Student. In questo test si fa la differenza tra le medie
(m) e la si divide per l’errore standard (se), che ricordiamo essere uguale alla deviazione standard (sd) divisa
per la radice quadrata del numero di osservazioni:
mplac − mf arm
se
che può essere scritta più in dettaglio, per campioni di pari numerosità, come segue
mplac − mf arm
q
2
sdplac /nplac + sd2f arm /nf arm
Il senso di questo test è che il valore diventa tanto più grande quando più è grande la differenza tra le medie e
quando più è piccoloa la variabilità nei campioni (cioè l’errore standard). Quindi, a parità di errore standard,
un valore elevato del test significa una grande differenza tra le medie. Abbiamo già capito quindi che un
valore elevato nel test t farà propendere per l’improbabilità che le medie delle popolazioni di origine siano
uguali. Il valore del test può risultare elevato, a parità di differenza delle medie, anche se la variabilità delle
misure è ridotta. Il senso è che una differenza tra le medie ha un diverso valore se la variabilità della misura è
grande o piccola. Infatti una data differenza tra le medie può essere casuale se le misure sono molto variabili
tra loro, mentre va presa molto sul serio se le singole misurazioni sono molto simili tra loro.
A titolo di esempio calcoliamo il test t per i nostri campioni, ricordando che l’ipotesi nulla è che la media
della popolazione a cui appartiene il gruppo ‘Placebo’ è uguale alla media della popolazione a cui appartiene
il gruppo ‘Farmaco’.
100 − 91
t= p
= 3.3
100/20 + 49/20
Il dr. Gosset (in arte “student”) ha calcolato pazientemente agli inizi del 1900 la probabilità che “t” assuma
un certo valore quando è vera l’ipotesi nulla. “t” ha un significato diverso con numerosità diverse dei campioni
(dato che determina i “gradi di libertà”), pertanto sono stati fatti i calcoli delle probabilità per diversi gradi
di libertà. In questo esempio i gradi di libertà sono nplac − 1 + nf arm − 1, quindi 38. Nella tabella sopra
riprodotta utilizziamo la riga con il numero di gradi di libertà più vicino (ed inferiore) ai nostri 38, quindi
quella con 30 gradi di libertà: vediamo che 3.3 è compreso tra gli ultimi due numeri, 2.75 e 3.646, i quali a
loro volta corrispondono ad una p di 0.01 e 0.001. Quindi la probabilità di ottenere in nostri dati quando
l’ipotesi nulla è vera è compresa tra 0.01 (1%) e 0.001 (0.1%). E’ quindi molto poco probabile che i nostri dati
siano compatibili con l’ipotesi nulla, che quindi rifiutiamo e di conseguenza rifiutiamo anche che la pressione
diastolica dei pazienti che assumo il placebo sia uguale alla pressione diastolica dei pazienti che assumo il
farmaco. La conclusione è che il farmaco testato è più efficaced del placebo.
8
Un esempio di test di ipotesi con dati nominali: il test del χ2
Spesso si è interessati a confrontare i dati che derivano da due set di dati nominali. Ad esempio potremmo
essere interessati a sapere se un corso di fromazione del personale sanitario sulla relazione di aiuto ha avuto
come conseguenza una maggior soddisfazione dei pazienti di una Unità Operativa. A tale scopo si sono
raccolti i dati di Soddisfazione dell’utente in un periodo precedente ed in uno successivo allo svolgimento del
corso di formazione. In questo caso abbiamo due variabili nominali: * il periodo di rilevazione dei dati può
essere codificato come “prima” e “dopo” il corso; * la soddisfazione dei pazienti può essere espressa come “1”
(soddisfatto) o “0” (non soddisfatto).
Di seguito l’elenco dei primi 10 e degli ultimi 10 soggetti intervistati.
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
1
2
3
4
5
6
7
8
9
10
1161
1162
1163
1164
1165
1166
1167
1168
1169
1170
soddisfazione periodo
1
prima
1
prima
0
prima
1
prima
1
prima
0
prima
0
prima
1
prima
1
prima
1
prima
1
dopo
1
dopo
1
dopo
1
dopo
1
dopo
0
dopo
1
dopo
1
dopo
1
dopo
1
dopo
I dati di questo tipo si possono rappresentare efficacemente in una tabella di contingenza. Nel caso più
semplice, come nel nostro esempio, ci sono due variabili nominali, i cui esiti sono espressi nelle righe per una
variabile e nelle colonne per l’altra.
Table 2: Tabella frequenze (assolute) osservate
insoddisfatti
soddisfatti
Totale
prima
dopo
Totale
113
407
520
106
544
650
219
951
1170
Da questa tabella desumiamo che sono stati rilevate le opinini di 520 e 650 pazienti rispettivamente prima e
dopo lo svolgimento del corso. Le informazioni che possiamo trarre da questa modalità di presentazione sono
però scarse se esprimiamo i dati come frequenza assoluta. Vediamo quindi la stessa tabella con le freqhenze
percentuali.
9
Table 3: Tabella frequenze (percentuali) osservate
prima
dopo
22 %
78 %
16 %
84 %
insoddisfatti
soddisfatti
Questo dato è molto più leggibile. Possiamo infatti vedere che dopo il corso di formazione la percentuale
di insoddisfatti (rispetto al totale dei pareri ricevuti in ciascun periodo) è scesa dal 22% al 16%. Come
sempre dobbiamo cercare di prevedere se il risultato ottenuto in questo campione può essere considerato
valido per tutta la popolazione dei pazienti che saranno ricoverati in questa Unità Operativa. In altre parole,
la riduzione degli insoddisfatti è proprio legata all’effetto del corso oppure può essere spiegata anche dalla
casualità? Quanto è probabile che il corso sia stato di per sè inefficace e che, per puro caso, nel periodo
‘prima’ abbiamo intervistato un campione di pazienti con molti “criticoni”, mentre nel periodo “dopo”, sempre
per puro caso, abbiamo intervistato un campione con molti soggetti “accomodanti” e quindi più facili da
accontentare? L’analisi statistica ci aiuta a rispondere a questa domanda. Per prima cosa formuliamo la
nostra IPOTESI NULLA: la percentuale degli insoddisfatti prima e dopo il corso di formazione è uguale.
Espressa formalmente l’ipotesi nulla è: H0 : probabilitàinsoddisf atti−prima = probabilitàinsoddisf atti−dopo .
Nella tabella di contigenza con le frequenze assolute, possiamo vedere che il totale degli insoddisfatti totale
(che comprende cioè entrambi i periodi) è di 219 soggetti su 1170, cioè il 18.72%. Se fosse vera l’ipotesi nulla,
questa percentuale dovrebbe essere uguale prima e dopo il corso di formazione. Per cui, sotto ipotesi nulla, ci
dovremmo aspettare che siano insoddisfatti il 18.72% dei 520 soggetti intervistati prima ed il 18.72% dei 650
pazienti intervistati dopo il corso. Se questa fosse la verità, dovremmo ridisegnare la tabella di contingenza
con le frequenze attese se in entrambi i periodi i soggetti avessero la stessa percentuale di insoddisfazione
(pari a quella totale).
Table 4: Tabella frequenze (assolute) attese
insoddisfatti
soddisfatti
prima
dopo
97.3
422.7
121.7
528.3
Il confronto tra le celle corrispondenti delle due tabelle (frequenze osservate ed attese) mostra valori differenti.
Ad esempio abbiamo contato 113 insoddisfatti prima del corso mentre ce ne saremmo aspettati 97.3 sotto
ipotesi nulla. Dopo il corso gli insoddisfatti erano 106, ma sotto ipotesi nulla ce ne raremmo aspettati 121.7.
Per conoscere la probabilità che queste differenze siano dovute alla casualità del campionamento, possiamo
fare un test statistico. In questo caso un test appropriato è il test del χ2 (si legge “chi quadrato”). In questo
test si calcola per ciascuna cella della tabella di contingenza il quadrato delle differenze tra i valori osservati e
2
quelli attesi, e lo si divide per il valore atteso ( (osservato−atteso)
), come si vede nella prossima tabella.
atteso
insoddisfatti
soddisfatti
prima
dopo
2.5332991
0.5831322
2.025390
0.466572
Il valore del test chi2 è dato dalla somma di tutti questi valori presenti nella tabella:
χ2 =
rc
X
(osservato − atteso)2
atteso
i=1
Nel nostro esempio la somma è 5.61. A questo punto dobbiamo vedere quanto è probabile ottenere questo
10
valore quando è vera l’ipotesi nulla. Fortunatamente anche per la distribuzione del χ2 sono state calcolate le
probabilità che i differenti valori possono assumere quando è vera l’ipotesi nulla. Nel nostro esempio abbiamo
un grado di libertà, quindi cerchiamo di associare una probabilità al risultato ottenuto cercando nella prima
riga.
Il nostro valore di 5.61 è compreso tra 5.41 e 6.63, i quali sono associati rispettivamente probabilità di 0.01
(cioè 1 su 100=1%) e di 0.02 (cioè 1 su 200=0.5%). Ciò vuol dire che la probabilità di osservare i nostri dati
(o dati ancor più diversi da quelli definiti nell’ipotesi nulla) è compresa tra 0.5% e 1% quando è vera l’ipotesi
nulla. Una probabilità molto bassa, che ci porta a rifiutare H0 . Quindi concluderemo che è molto improbabile
che le differenze che osserviamo nella tabella dei dati osservati siano dovute alla casualità. Pertanto dobbiamo
ragionevolmente ritenere che il corso di formazione abbia funzionato.
Gli studi clinici
La comprensione dei concetti di esposizione ed outcome (esito) in ambito epidemiologico è di importanza
fondamentale per comprendere il disegno degli studi. In epidemiologia l’esposizione è un evento che può
influenzarne un altro, che vie definito outcome (esito). L’esposizione, talora definita fattore di rischio, ha una
vasta gamma di significati: può essere un fattore ambientale (inquinamento, attività lavorativa, . . . ), oppure
inerente al paziente (gruppo sanguigno, sesso, età, razza,..), oppure un trattamento o una strategia sanitaria
L’outcome è anch’esso un termine generico che può indicare qualsiasi evento correlato alla salute/malattia (la
diagnosi di malattia, un certo stato di salute, la morte o la sopravvivenza).
Si possono descrivere due grandi categorie di studi, quelli osservazionali e quelli sperimentali. Negli studi
osservazionali il ricercatore si limita ad osservare l’andamento dei fenomeni per poter trarre conclusioni.
Negli studi sperimentali invece lo sperimentatore compie interventi diretti, manipola cioè le condizioni della
ricerca applicando strategie terapeutiche o preventive a due o più gruppi di soggetti.
11
Gli studi osservazionali.
Studi descrittivi
Il livello più semplice di studio osservazionale sono gli studi descrittivi. Gli studi descrittivi rilevano fenomeni
che si presentano nella collettività senza confrontare tra loro gruppi differenti di individui Pertanto non
possono avere lo scopo di analizzare eventuali associazioni tra esposizioni ed outcome.
Case report e serie di casi Il livello più semplice di studio descrittivo è il “case report”. Nel case report è
descritto dettagliatamente il caso di un singolo individuo che presenta una malattia insolita o l’apparente
associazione tra un’esposizione ed una malattia non descritta in precedenza. Un case report non produce
nuove conoscenze affidabili, ma può suggerire di condurre studi con un disegno più robusto.Per esempio, un
medico ha descritto la comparsa di adenoma epacellulare benigno in donne che avevano assunto contraccettivi
orali. Un successivo studio caso-controllo ha confermato una forte associazione tra l’uso a lungo termine di
pillole alte dosi e questo raro tumore. Si parla di serie di casi quando si descrivono più casi individuali
che condividono una stessa caratteristica. Per esempio l’osservazione di diversi casi di immunodeficienza in
maschi omosessuali a Los Angeles ha portato a considerare l’epidemia di AIDS negli Stati Uniti.
Studi di prevalenza (trasversali, cross-sectional). Gli studi di prevalenza descrivono la salute di una
popolazione. In questi studi si raccolgono nel medesimo momento esposizioni ed outcome, pertanto non sono
in grado di stabilire con chiarezza se l’esposizione ha preceduto l’outcome, ad eccezione di esposizioni di lunga
durata (meglio se dalla nascita), come ad esempio sesso e gruppo ematico.
12
Studi di sorveglianza. In questi studi si ha la rilevazione sistematica e ripetuta nel tempo di dati relativi
alla salute. L’analisi e l’interpretazione di questi dati è spesso di grande importanza nel decidere gli interventi
sanitari da mettere in atto. La sorveglianza può essere attiva o passiva. La sorveglianza passiva acquisisce i
casi di interesse da registri statistici ufficiali, come per esempio quelli anagrafici, mentre la sorveglianza attiva
va alla ricerca dei casi di interesse con tutti i mezzi disponibili.
Gli studi descrittivi hanno il vantaggio di utilizzare dati già disponibili e quindi sono efficienti e poco costosi.
Devono essere considerati come il primo approccio allo studio di una condizione. Possono essere utili per
generare ipotesi, ma da essi non si possono trarre conclusioni sull’associazione e tantomenao sulla relazione
causa-effetto tra una esposizione ed un outcome.
Gli studi analitici
Negli studi analitici è presente il confronto tra soggetti appartenenti a gruppi diversi. Essi sono
distinti tra loro in base alla rilevazione temporale di esposizione ed outcome.
• Studi di prevalenza (trasversali, cross-sectional). In questa tipologia di studio esposizione ed
outcome sono rilevati nello stesso tempo. Può quindi essere definito di prevalenza sia uno studio
descrittivo, quando si stima la frequenza di una condizione in una popolazione (in questo caso è uno
studio descrittivo, vedi sopra), sia uno studio analitico, quando si rileva la presenza di esposizione
ed outcome in gruppi diversi. Negli studi cross-sectional la relazione temporale tra esposizione ed
outcome può non essere chiara, essendo rilevati nello stesso momento. Per esempio, se uno studio
cross-sectional rilevasse che l’obesità è più frequente tra le donne con artrosi rispetto a quelle senza
artrosi, non potremmo definire se è l’eccessivo peso sulle articolazioni che determina l’artrosi, oppure se
è l’artrosi che riduce il movimento e quindi favorisce l’obesità. Pertanto gli studi trasversali poco si
prestano a definire relazioni causa-effetto.
• Studi di coorte. Gli studi di coorte definiscono prima un gruppo (una coorte) di soggetti con
l’esposizione di interesse ed un gruppo (una coorte) di soggetti senza questa esposizione. I ricercatori
seguono nel tempo i soggetti di ciascuna coorte e rilevano l’incidenza dell’outcome. Se l’incidenza
13
dell’outcome è maggiore nella coorte degli esposti, si può concludere che l’esposizione è associata ad un
aumento del rischio dell’outcome. Gli studi di coorte sono poco efficienti quando l’outcome è molto
raro (bisogna studiare coorti molto grandi per osservare un sufficiente numero di esiti) o richiede tempi
molto lunghi per svilupparsi (sono necessari tempi molto lunghi di osservazione).
• Studi caso-controllo. Negli studi caso-controllo si identifica un gruppo di soggetti che hanno manifestato una malattia (casi) ed un gruppo che invece non ha mai avuto questa malattia (controlli), quindi
sia per i casi che per i controlli si ricercano nel passato le esposizioni che potrebbero essere associate
all’outcome oggetto dello studio. Se la prevalenza dell’esposizione è più frequente nei casi rispetto ad i
controlli, l’esposizione è associata ad un aumento del rischio dell’outcome. Gli studi caso-controllo sono
particolarmente utili nei casi in cui gli studi di coorte sono poco efficienti, cioè in caso di malattie rare o
con lunghi tempi di insorgenza. Questa condizione si verifica, ad esempio, quando si studiano malattie
cardiovascolari o tumorali. Il punto cruciale degli studi caso-controllo è la scelta di un appropriato
gruppo di controllo. Sono quindi molto esposti al rischio di errore sistematico (vedi sotto). Gli studi
caso-controllo non possono determinare la incidenza dell’outcome: nei casi infatti il 100% dei soggetti
deve avere l’outcome, mentre nei controlli nessuno deve averlo. Per questo motivo non si possono
calcolare le misure di rischio ed al loro posto per misurare le associazioni viene utilizzato l’odds ratio,
che è molto simile al rischio relativo qualora l’outcome sia raro.
Gli studi sperimentali.
Gli studi sperimentali si possono dividere in due categorie principali:
• Studi non randomizzati. Alcuni trials sperimentali non assegnano casualmente l’esposizione (cioè
il trattamento), ma i soggetti sono stati scelti per essere inseriti nel gruppo di trattamento (con
l’esposizione) o nel gruppo di controllo (senza l’esposizione). Questi studi sono esposti al rischio di bias
di selezione (vedi sotto) e sono condotti ed analizzati similmente agli studi di coorte.
• Studi randomizzati e controllati. Rappresentano il disegno di studio generalmente ritenuto di
miglior qualità. Differentemente dagli studi non randomizzati, l’esposizione (trattamento/prevenzione)
viene assegnata casualmente ai soggetti che partecipano allo studio con una procedura che è definita
randomizzazione. Se la randomizzazione è effettuata correttamente, si evita ragionevolmente di avere un
bias di selezione: infatti i pazienti nel gruppo di trattamento e nel gruppo di controllo dovrebbero avere
caratteristiche simili tra loro, perchè ogni individuo deve avere la stessa probabilità di essere inserito in
ciascuno di questi gruppi. Inoltre anche i confondenti (sia conosciuti che sconosciuti) sono probabilmente
distribuiti equamente nei gruppi di studio: l’assegnazione casuale farà si che ogni confondente abbia
la medima probabilità di capitare nei trattamenti o nei controlli. Il maggior problema degli studi
controllati e randomizzati è solitamente una ridotta validità esterna. I trial randomizzati infatti possono
arruolare solo volontari che superano un processo iniziale di screening. Il campione dei soggetti che
partecipano allo studio potrebbe quindi non essere veramente rappresentativo della popolazione alla
quale si vogliono generalizzare le conclusioni.
L’interpretazione dei risultati
Gli studi epidemiologici e clinici possono presentare “difetti” di progettazione che possono pregiudicare (anche
radicalmente) la corretta interpretazione dei risultati. Esaminiamo alcuni aspetti.
• Errore sistematico (bias). Tutti gli studi osservazionali sono caratterizzati da bias. E’ necessario
valutarli criticamente per capire in che modo possono aver influenzato i risultati.
• Bias di selezione. I gruppi sono simili in tutti gli aspetti importanti? Il bias di selezione rischia di
non rendere confrontabili i gruppi. Ad esempio sia studi di coorte che caso-controllo avevano suggerito
che lo jogging dopo un infarto del miocardio preveniva una recidiva dell’infarto. Un successivo trial
randomizzato e controllato non ha confermato questo beneficio. I pazienti che scelgono di fare esercizio
14
potrebbero infatti differire da chi non fa sport per caratteristiche importanti, come ad esempio la dieta
od il fumo.
• Bias di informazione (osservazione, classificazione, misurazione). Scorretta attribuzione dell’outcome
o dell’esposizione. Può verificarsi se si raccolgono informazioni in maniera diversa (ad esempio al letto
del paziente nei casi e telefonicamente nei controlli). Il bias di sospetto diagnostico si ha quando la
conoscenza di una presunta causa di malattia può portare ad una più approfondita ricerca tra gli esposti,
come ad esempio la ricerca dell’infezione da HIV nei soggetti che hanno utilizzatto sostanze per via
endovenosa. Oppure la presenza di una malattia potrebbe indurre a cercare una presunta esposizione di
interesse, come il fumo nei casi di tumore al polmone. Per minimizzare il rischio di bias di informazione,
le informazioni sull’esposizione negli studi caso controllo dovrebbere essere raccolte da ricercatori che
non sanno se il soggetto in questione è un caso o un controllo. Allo stesso modo in uno studio di coorte,
lo sperimentatore che rileva l’outcome dovrebbe essere all’oscuro dell’esposizione di ogni partecipante.
Negli studi caso-controllo, il bias di memoria può essere importante in caso di esposizioni lontane nel
tempo. I casi infatti tendono a ricercare con particolare attenzione una possibile esposizione associata
alla loro malattia, mentre i controlli sono meno motivati a farlo.
• I confondenti. Quando ricercatore cerca di correlare un’esposizione all’outcome, può invece misurare
l’effetto di un terzo fattore chiamati confondente. Una variabile confondente è associata con
l’esposizione ed influenza l’outcome, ma non è un legame intermedio tra esposizione ed outcome.
Ad esempio, i primi studi sui contraccettivi orali rilevarono un marcato incremento di rischio di infarto
del miocardio. Successivamente si dimostrò che l’associazione era dovuta la fatto che c’era un maggior
numero di fumatrici tra chi utilizzava i contraccettivi rispetto a chi non li utilizzava. Quindi il fumo di
sigaretta confondeva la relazione tra contraccettivi orali e infarto.
• Validità interna. E’ la capacità di uno studio di misurare realmente cosa si era programmato di
misurare. La validità interna di uno studio è irrimediabilmente abbattuta dalla presenza di bias di
informazione o di selezione. Al contrario, la presenza di confondenti può essere corretta se il confondente
è conosciuto. Si può ricorrere a tre principali approcci: il matching, la stratificazione o l’analisi
multivariata. Negli studi caso-controllo il matching prevede l’accoppiamento di un caso con un controllo
che abbia la stessa presenza/assenza del confondente. Ad esempio, se il confondente fosse il fumo, ogni
coppia caso-controllo deve avere lo stesso comportamento nel fumo di sigaretta. La stratificazione
consente di controllare per il confondente dopo il completamento dello studio, se ad esempio si analizzano
i risultati separatamente nei fumatori e nei non fumatori. Con le tecniche multivariate invece un modello
matematico esamina il potenziale effetto di una variabile a parità di tutti gli altri fattori. Il vantaggio è
che può “controllare” contemporaneamente la presenza di più possibili confondenti.
• Validità esterna. I risultati di uno studio possono essere generalizzati per i pazienti di chi legge lo
studio? In altre parole, si può passare dal campione alla popolazione? Uno studio ha una buona validità
esterna se chi compone il campione oggetto di indagine ha le stesse caratteristiche della popolazione. I
trial randomizzati e controllati sono probabilmente meno a rischio di errori sistematici rispetto agli studi
osservazionali, ma possono avere una minor validità esterna a causa della selezione dei partecipanti.
• La valutazione delle associazioni. La presenza di bias di selezione, bias di informazione o di
confondenti può produrre risultati altamente significativi anche se fasulli. Qualora uno studio produca
risultati significativi pur senza essere affetto da problemi di validità interna, dobbiamo anche tenere
presente che la possibile spiegazione del raggiungimento della significatività statistica potrebbe essere il
caso. Infatti il valore di p misura la probabilità di ottenere una conclusione falsamente positiva: una
differenza rilevata nello studio, sebbene questa non esista nella popolazione (errore di tipo I o errore
α). Pertanto quando si evidenzia una associazione statisticamente significativa, bisogna valutare se
esista realmente una relazione causa-effetto tra esposizione ed outcome. Perchè questa possa sussistere
è fondamentale il criterio di temporalità: la causa deve precedere l’effetto, cosa non sempre semplice
da stabilire in caso di malattie croniche. E’ anche improbabile che non vi sia nesso causale quando
l’associazione tra esposizione ed outcome è molto forte (ad esempio un rischio relativo superiore a 3
o un odds ratio superiore a 4). Un altro elemento che conferma la reale associazione tra esposizione
ed outcome è la ripetizione dei risultati in popolazioni diverse e con disegni di studio differenti. Altri
15
elementi a favore di una relazione causale tra esposizione ed outcome sono la presenza di una relazione
dose-risposta (tanto più elevata è l’entità dell’esposizione, tanto maggiore è la frequenza dell’outcome),
la plausibilità biologica (cioè la spiegazione biologica del fenomeno) e la coerenza con le conoscenze
acquisite in precedenza.
Le meta-analisi
Se vi sono vari studi condotti nel mondo sullo stesso quesito, la meta-analisi (in inglese “meta analysis”
o anche “overview”) permette di valutare i risultati in maniera integrata. Tramite la meta-analisi, la
comunità scientifica può rivedere sistematicamente tutta l’evidenza prodotta dalla ricerca su un dato quesito,
e può ottenere una valutazione quantitativa e qualitativa dell’effetto di un dato trattamento considerato in
vari studi. La meta-analisi è quindi la metodologia che permette di raccogliere tutti i dati prodotti da vari
studi sullo stesso argomento e di analizzarli con metodi appropriati al fine di ottenere una risposta globale. A
volte questa proposta è conclusiva, e porta a individuare quindi il trattamento “di elezione” per una certa
patologia. Altre volte invece l’evidenza raccolta da vari studi non è sufficiente a motivare la scelta di un
dato trattamento, ma rivela quali siano gli aspetti che ancora necessitano di approfondimento. In questo
caso, i risultati della meta-analisi sono il punto di partenza per la pianificazione di uno studio che possa far
ulteriormente avanzare la conoscenza ed essere conclusivo sulle questioni ancora aperte. Vediamo un esempio.
Nella figura è riportata la presentazione dei dati raccolti ed elaborati in una meta-analisi.
Essa riassume i dati relativi a 11 diversi studi nei quali pazienti con una storia di infarto miocardico erano
stati randomizzati a ricevere un trattamento prolungato (di un mese o più) con antitrombotici verso nessun
trattamento. Per ciascun studio, identificato con un nome in prima colonna, sono riportati: il tipo di
trattamento (seconda colonna), il numero di eventi/numero di soggetti randomizzati nei due gruppi (terza e
quarta colonna), dove si considera come evento l’infarto miocardico o l’ictus cerebrale (stroke) non fatali
oppure la morte per causa vascolare. I totali riportati alla base delle colonne danno una stima globale della
probabilità di evento nei due gruppi di trattamento: 13% di eventi nel gruppo AP (1331/9877) e 17% nel
gruppo di controllo (1693/9914), con una riduzione assoluta a favore dei trattati del 4% nella mortalità
e morbidità vascolare. Il principio su cui si basa la meta-analisi è che, se un certo tipo di trattamento
fosse legato a un reale beneficio, allora, al di là di eccezioni possibilmente imputabili al caso, i risultati di
studi diversi dovrebbero verosimilmente puntare verso la stessa direzione di beneficio (pur non raggiungendo
necessariamente la significatività statistica). Quindi, con la meta-analisi si combinano i risultati di vari studi
16
per ottenere una valutazione statistica globale che possa avere una applicabilità generale nella pratica clinica.
In questo esempio, i risultati di tutti gli studi puntano nella stessa direzione di beneficio del trattamento e non
risulta esservi eterogeneità statisticamente significativa tra i risultati singoli, come indicato nel test riportato
sotto i totali. Le stime dell’effetto del trattamento in ciascuno studio e globali sono rappresentate graficamente
in termini di “odds ratio”, con intervalli di confidenza. La linea verticale continua, tracciata in corrispondenza
di un odds ratio unitario, indica la posizione di equivalenza del trattamento con antitrombotici rispetto al
non trattamento. Un odds ratio inferiore a 1, e quindi alla sinistra di detta linea, indica che il trattamento
è protettivo, mentre il trattamento risulterebbe dannoso se l’odds ratio fosse superiore a 1. Come si vede
dal grafico, gli odds ratio stimati in ciascuno studio, e indicati con dei quadratini, sono tutti concordemente
inferiori all’unità. L’area dei quadratini è proporzionale alla informatività dello studio, cioé alle sue dimensioni
(o meglio al numero degli eventi) e quindi un’area più grande indica che i risultati dello studio corrispondente
avranno più peso nella stima globale dell’effetto del trattamento. Le linee continue orizzontali rappresentano
gli intervalli di confidenza al 99% dell’odds ratio del singolo studio. Quando attraversano la linea verticale
continua, indicano che il risultato dello studio è compatibile anche con l’ipotesi di equivalenza (cioé che l’odds
ratio non sia significativamente diverso da 1, al livello alfa = 0.01). Come si vede nella figura, solo 2 degli
11 studi forniscono stime dell’effetto del trattamento significative al livello 0.01. Tuttavia, combinando i
singoli risultati in una media opportunamente pesata (in base alla varianza), si ottiene una stima globale
basata su molte osservazioni e i cui limiti di confidenza sono molto ristretti. L’odds ratio globale risulta essere
0.75 ed è rappresentato dalla linea tratteggiata. Esso corrisponde ad una riduzione percentuale dell’odds
di evento vascolare del 25% nel gruppo dei trattati rispetto ai non trattati. I limiti di confidenza al 95%,
molto piccoli, sono rappresentati col rombo disegnato sulla linea tratteggiata. Il dibattito sul ruolo che la
meta-analisi ha avuto in vari campi della ricerca clinica (in particolare nelle patologie cardiovascolari ed
oncologiche) e che potrà avere in futuro è a tuttoggi molto aperto. In particolare, varie critiche sono mosse
a questa metodologia, poiché vari sono i problemi che possono influenzare la validità ed accettabilità delle
conclusioni da essa tratte. I problemi riguardano principalmente i criteri di inclusione/esclusione degli studi
in relazione al loro livello di qualità scientifica, l’influenza dell’eterogeneità dei pazienti sulle stime ed altri
aspetti legati alla generalizzabilità ed applicabilità dei risultati.
La piramide delle evidenze
I differenti tipi di studi possiedono una differente livello di credibilità ed autorevolezza. Questo concetto è
riassunto nella figura sottostante.
Come si può osservare case report e serie di casi sono il tipo di studi meno autorevole, mentre i trial
randomizzati e controllati sono il disegno di studio a cui viene attribuita la massima credibilità. La posizione
delle meta-analisi è controversa. Per alcuni sono il più elevato livello di evidenza, mentre altre correnti di
17
pensiero mettono in discussione questa posizione. Il disegno dello studio determina la qualità della evidenza
degli studi. Questo è tenuto in grande considerazione nella creazione delle linee guida, in cui la forza delle
raccomandazioni è molto influenzata dalla qualità delle evidenze.
18