ITIS OMAR
Dipartimento di Meccanica
ESAMI DI MATURITA’ TECNICA INDUSTRIALE
Indirizzo: Meccanica
Tema di MECCANICA APPLICATA ALLE MACCHINE
1995
Un motore diesel a quattro tempi, funzionante 2200 giri/min, aziona, mediante cinghie trapezoidali,
una pompa che a 3000 giri/min elabora 0.030 m3/s di acqua con una prevalenza di 55 m.
Il candidato, assumendo con opportuno criterio ogni altro dato occorrente, esegua il
proporzionamento della trasmissione, determinando inoltre:
S
S
la potenza che deve fornire il motore;
lo sforzo esercitato dalle cinghie sugli alberi delle pulegge.
Durata massima della prova: 8 ore
Durante lo svolgimento della prova è consentito soltanto l’uso di tavole numeriche, manuali tecnici, regolo calcolatore
e calcolatrici portatili non programmabili.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.
Relazione di calcolo
Determinazione della potenza assorbita
(
h
Q
N
g
massa specifica dell’acqua
prevalenza
portata
potenza
accelerazione di gravità
1
kg/dm3
55 m
0.03 m3/s
kW
~10 m/s2
γ ⋅ g ⋅ Q ⋅ 103 ⋅ h
N=
= 16.2
1000
kW
Assunto un rendimento globale 0 dell’impianto pari a 0.65, la potenza Nm che deve fornire il motore
vale:
Nm =
N 16.2
=
≅ 25 kW
η 0.65
Determinazione, in prima approssimazione, dei diametri collegati al motore dm e alla pompa dp
Ipotizzando di usare un acciao C40 bonificato (tabella) con un carico di rottura R intorno a 700
N/mm2, in un calcolo di prima approssimazione si può fare affidamento su una tensione ammissibile a
torsione pari a1:
τ amm =
R ⋅ 0.05
≅ 20 N / mm2
3
Momento di uscita dal motore Mm
Mm =
N m 25000 ⋅ 60
=
= 108.5 Nm
ωm
2π ⋅ 2200
Momento di ingresso alla pompa Mp (si trascura il rendimento a favore della stabilità)
Mp =
1
N m 25000 ⋅ 60
=
= 80 Nm
ωp
2π ⋅ 3000
La tensione ammissibile è molto bassa perché, nella fase di progetto, si è trascurata totalmente la flessione
indotta dal tiro di cinghia.
E i diametri risultano:
dm =
dp =
3
3
16 ⋅ M m
=
π ⋅ τ amm
16 ⋅ M p
π ⋅ τ amm
=
3
16 ⋅ 108.5 ⋅ 103
≅ 30 mm
π ⋅ 20
3
16 ⋅ 80 ⋅ 103
≅ 27 mm
π ⋅ 40
Determinazione della trasmissione a cinghia
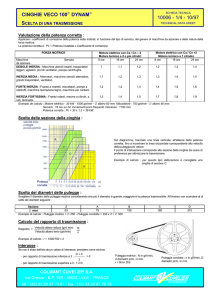
Dalla tabella allegata, nota la velocità di rotazione e la potenza motore, si ricava il tipo di
cinghia da utilizzare:
cinghie di sezione tipo B
Diametri primitivi delle pulegge
d p = 140 mm
Dp = 190
mm
La velocità v della cinghia risulta pari a 22 m/s
Interasse approssimato Ia
Ia =
Dp + d p
2
+ d p = 305 mm
Lunghezza di calcolo della cinghia Lc
(
Dp − d p
π
Lc = ( Dp + d p ) +
2
4 ⋅ Ia
)
2
+ 2 I a = 1130.4 mm
Lunghezza disponibile di cinghia Ld = 1135 mm (tabella)
Interasse corretto Ic
Ic = Ia +
Ld − Lc
= 352.3 mm
2
Diametro primitivo equivalente de (tabella)
d e = d p ⋅ Fb = 140 ⋅ 11
. = 154 mm
Ricavati i coefficienti Fe (tabella) e F" (tabella), la potenza nominale trasmissibile da una cinghia
p1 si determina in funzione della sua potenza nominale (tabella)
p1 = pot ⋅ Fe ⋅ Fα = 4.3 ⋅ 0.95 ⋅ 0.865 = 3.53 kW
Potenza di calcolo Pc (tabella)
Pc = N m ⋅ Fs = 25 ⋅ 12
. = 30 kW
Numero cinghie nc
nc =
Pc
30
=
≅8
p1 3.53
Determinazione del tiro di cinghia
Il tiro della cinghia a riposo T0 vale1:
T0 = (12
. ÷ 15
. )⋅
Mp
Dp
= 631 N
Ritenuti i rami di cinghia paralleli, la forza radiale totale F agente sull’albero vale:
F = 2 ⋅ T0 = 1262 N
L’ingombro assiale L della puleggia, tenuto conto del numero di cinghia, è approssimativamente:
(tabella)
L = (nc − 1) ⋅ e + 2 f = 7 ⋅ 19 + 2 ⋅ 12.5 = 158 mm
La tensione di flessione indotta dal tiro di cinghia può essere ritenuta pari a2:
σf =
Mf
Wf
=
32 ⋅ ( F ⋅ 12
. ⋅ L / 2)
π ⋅d
3
p
≅ 62 N / mm 2
La tensione di torsione vale:
τ =
16 ⋅ M t
2
3 = 21 N / mm
π ⋅ dp
La tensione ideale vale:
σ id = σ 2f + 3τ 2 = 72 N / mm2
1
Indicato con M il momento torcente trasmesso e con D il diametro primitivo della puleggia, il tiro di cinghia a
riposo T0 , può essere posto pari a:
T0 = (1.2 ÷ 15
.)
M
D
M
D
M
T0 = ( 2 ÷ 2.5)
D
T0 = ( 4 ÷ 5)
2
puleggia
cinghie trapezoidali
cinghie piatte
cinghie piatte con tenditori
Il momento flettente è stato aumentato del 20% per tener conto della distanza tra il cuscinetto e il fianco della
Numero cinghie nc
nc =
Pc
30
=
≅8
p1 3.53
Determinazione del tiro di cinghia
Il tiro della cinghia a riposo T0 vale1:
T0 = (12
. ÷ 15
. )⋅
Mp
Dp
= 631 N
Ritenuti i rami di cinghia paralleli, la forza radiale totale F agente sull’albero vale:
F = 2 ⋅ T0 = 1262 N
L’ingombro assiale L della puleggia, tenuto conto del numero di cinghia, è approssimativamente:
(tabella)
L = (nc − 1) ⋅ e + 2 f = 7 ⋅ 19 + 2 ⋅ 12.5 = 158 mm
La tensione di flessione indotta dal tiro di cinghia può essere ritenuta pari a2:
σf =
Mf
Wf
=
32 ⋅ ( F ⋅ 12
. ⋅ L / 2)
π ⋅d
3
p
≅ 62 N / mm 2
La tensione di torsione vale:
τ =
16 ⋅ M t
2
3 = 21 N / mm
π ⋅ dp
La tensione ideale vale:
σ id = σ 2f + 3τ 2 = 72 N / mm2
1
Indicato con M il momento torcente trasmesso e con D il diametro primitivo della puleggia, il tiro di cinghia a
riposo T0 , può essere posto pari a:
T0 = (1.2 ÷ 15
.)
M
D
M
D
M
T0 = ( 2 ÷ 2.5)
D
T0 = ( 4 ÷ 5)
2
puleggia
cinghie trapezoidali
cinghie piatte
cinghie piatte con tenditori
Il momento flettente è stato aumentato del 20% per tener conto della distanza tra il cuscinetto e il fianco della
a cui corrisponde un coefficiente di sicurezza > pari a:
ξ=
pienamente accettabile.
700
= 9.7
72