Cambiamenti di stato
Equilibri tra le fasi:
•diagrammi di stato per un componente puro
•diagrammi di stato a due componenti
1
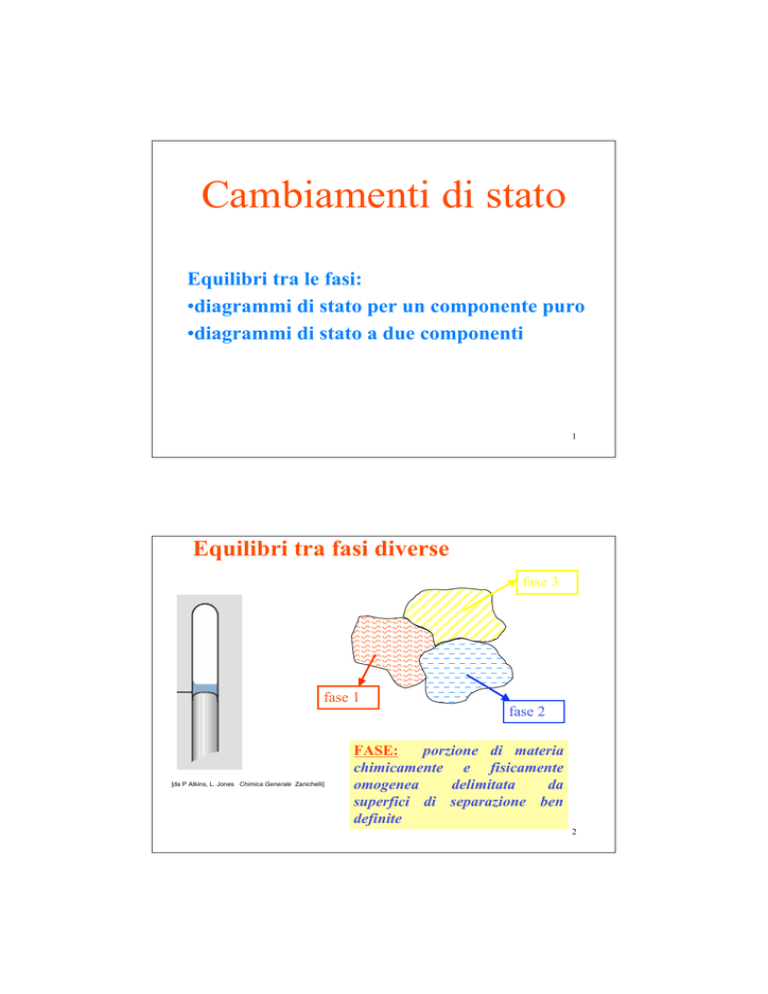
Equilibri tra fasi diverse
fase 3
fase 1
[da P Atkins, L. Jones Chimica Generale Zanichelli]
fase 2
FASE:
porzione di materia
chimicamente e fisicamente
omogenea
delimitata
da
superfici di separazione ben
definite
2
Cambiamento di stato (o di fase)
Passaggio (trasferimento) di materia da
una fase ad un’altra.
Per una sostanza
pura, il cambiamento
da una fase (stato di
aggregazione) ad un
altro si chiama:
CAMBIAMENTO
DI STATO. Per una
sostanza pura questo
passaggio avviene a
temperatura costante.
VAPOR D’ACQUA (d = 0.00326 g/ml a 400°C)
Vaporizzazione
Sublimazione
ΔHvap = 40.67
kJ/mol
Condensazione
ACQUA LIQUIDA
(d = 0.997 g/ml a 25°C)
ΔHsub = 46.68
kJ/mol
Brinamento
Fusione
ΔH fus = 6.01
kJ/mol
Solidificazione
ACQUA SOLIDA (d = 0.917 g/ml a 0°C)
Variazione della temperatura in funzione del tempo
durante i cambiamenti di fase di una sostanza pura
3
4
Regola delle FASI (Gibbs)
La varianza (V) di un sistema corrisponde al numero delle
variabili indipendenti o gradi di libertà del sistema, cioè il numero
delle variabili che determinano completamente lo stato intensivo
del sistema stesso ed i cui valori possono essere variati
indipendentemente gli uni dagli altri senza che cambi il numero
delle fasi in equilibrio tra loro.
Se si considera C componenti distribuiti in F fasi, la regola delle
fasi ha la seguente espressione:
V=C+2-F
Se prendiamo in considerazione un sistema in cui una delle 2
variabili (T o P) risulta costante, allora la regola delle fasi
assumerà la seguente espressione:
V=C+1-F
5
Applicazioni della regola delle FASI
•Sistema a 1 componente puro, liquido in equilibrio con il suo
vapore
C=1 F=2
V=1+2–2=1
P e T sono legate tra loro da una relazione P = f (T)
•Sistema a 1 componente puro, presente in tre fasi in equilibrio tra
loro (es. acqua liquida, ghiaccio e vapor d’acqua – PUNTO TRIPLO)
C=1 F=3
V=1+2–3=0
P e T possono assumere solo una coppia di valori ben definiti!! Se
si altera una sola variabile, si ha la scomparsa di almeno una6 fase
Diagramma di stato a un componente
Se si riportano in un piano P-T le relazioni relative agli equilibri:
solido-vapore
liquido-vapore
solido- liquido
è possibile determinare i campi di esistenza delle diverse fasi e le
condizioni di equilibrio tra loro. Si ottiene in questo modo il
diagramma di stato o delle fasi.
La relazione esistente tra pressione e temperatura quando un
sistema è costituito da una sola specie presente in due fasi distinte
in equilibrio (varianza 1) è l’ equazione di Clausius-Clapeyron:
dP
!H
=
dT T " !V
ΔH = calore latente (a P costante)
ΔV = variazione di volume
7
Equazione di Clausius-Clapeyron
Equilibri fase vapore - fase condensata
solido ↔ vapore
ΔV = V(vap) – V(sol) ≅ V(vap)
liquido ↔ vapore
ΔV = V(vap) – V(liq) ≅ V(vap)
dP "H ! P
=
dT T ! RT
dP = !H dT
P
RT 2
ln P = ln A "
!H
RT
V ( vap ) =
P = A#e
"
RT
P
!H
RT
A è una costante che
varia da specie a specie
8
Diagramma di stato dell’acqua
P
P = A1 # e
"
"H sub > "H vap
!H sub
RT
!
Le due curve si incontrano
in un punto in cui si ha la
coesistenza delle 3 fasi
(punto triplo)
P = A2 # e
"
!H vap
RT
T
9
Equazione di Clausius-Clapeyron
Equilibri tra fasi condensate
solido ↔ liquido
dT T " !V
=
dP
!H
ΔHfus > 0
ΔV > 0 oppure ΔV < 0
dsol > dliq
dsol < d liq
dT/dP positiva
dT/dP negativa
Maggior parte delle sostanze
acqua
10
dsol < d liq
dT/dP negativa
dsol > dliq
dT/dP positiva
11
la densità del ghiaccio è minore di
quella dell’acqua perchè nel ghiaccio
si ha una struttura cristallina poco
compatta dovuta alla presenza di
legami ad idrogeno.
P
dT/dP < 0
liquido
1 atm
solido
[da P Atkins, L. Jones Chimica Generale Zanichelli]
0°C
T
12
P
B
PB
liquido
1 atm
A
solido
T
0°C
[da P Atkins, L. Jones Chimica Generale Zanichelli]
13
Diagramma di stato dell’acqua
Pressione
Equilibrio
solido-liquido
C
Liquido
Punto critico
218 atm, 374°C
Solido
Vapore
Equilibrio
solido-vapore
Equilibrio
liquido-vapore
Temperatura
Punto triplo
4.58 torr, 0.0098°C
A temperatura più alta di quella corrispondente al punto critico il
vapore non può condensare e quindi il liquido non può esistere,
14
qualunque sia la pressione.
Diagramma di stato dell’acqua
Temperatura normale di fusione ed ebollizione
Liquido
Pressione
Pressione:
1 atm
1 atm
Solido
Vapore
Temperatura
15
Diagramma di stato della CO2
dT/dP > 0
La pressione al punto triplo e di 5 atm, per cui se si riscalda da CO2
solido a pressione atmosferica si ha sublimazione (ghiaccio secco).
16
Sistemi a due componenti
Sistema a 2 componenti (A e B, es. Cu-Ni), occorre introdurre una
variabile CHIMICA (% in peso di A; XA) per descrivere la
COMPOSIZIONE del sistema.
Diagrammi tridimensionali nello spazio P-T- XA.
Per semplificare la rappresentazione, si usano diagrammi isobari
(P cost), isotermi (T cost) o a composizione costante.
P costante
*
TA
*
TB
0.0
0.2
0.4
0.6
0.8
1.0
XA
17
Proprietà colligative di soluzioni acquose
Per le soluzioni contenenti un soluto poco volatile, si osserva una diminuzione
della pressione di vapore rispetto al solvente puro.
Tale diminuzione risulta proporzionale alla frazione molare del soluto (ΔP ∝ XB)
Diagrammi a composizione costante
Innalzamento ebullioscopico
ΔTe:
"Te = K e ! m
Abbassamento crioscopico
ΔTc:
"Tc = K c ! m
m rappresenta la molalità della
soluzione, mentre Ke e Kc sono
chiamate rispettivamente
costante ebullioscopica e
crioscopica e dipendono solo
dalla natura del solvente 18
Diagrammi di stato a due componenti
Miscibilità completa allo stato liquido e
allo stato solido
Esempi: leghe Cu/Ni, Ag/Au, Au/Pt.
P costante
19
COSTRUZIONE DEL DIAGRAMMA Cu-Ni
20
Effetto della velocità di raffreddamento
Raffreddamento veloce: ZONATI
21
• La regola della leva fornisce il peso % delle fasi nelle due
regioni (quanto solido e quanto liquido ci sono)
Xs = OL
SL
Frazione in peso della fase solida
= Xs = w0 – wl
ws – wl
Xl =
OS
SL
Frazione in peso della fase liquida
= Xl = ws – w0
ws – wl
22
Temperatura
La regola della leva
Fase 1
M
T
F
N
Fase 2
P2
P1
XA=1
XA(1)
n1 FN
=
n2 MF
XA(tot)
XA(2)
XA=0
Il diagramma di stato fornisce informazioni non solo 23sulle
composizioni della fasi ma anche sulla quantità relativa delle stesse!
ESERCIZIO
Qual’è la quantità relativa in percentuale peso delle fasi solide e
liquide alla T di 1200 °C e per Ag = 70%? Si assuma che wl di Ag sia 74 e che ws
di Ag sia 64.
24
Diagrammi di stato a due componenti
Miscibilità completa allo stato liquido ma
completa immiscibilità allo stato solido
P costante
E= eutettico, al di sotto della temperatura eutettica non può esistere per il sistema
considerato una fase liquida.
Esempi: leghe Bi/Cd, Zn/Cd, Au/Tl
25
Diagrammi di stato a due componenti
Miscibilità completa allo stato liquido,
parziale miscibilità allo stato solido
P costante
Eutettico
Z’
tempo
Esempi: leghe Cu/Ag, Bi/Sn, Bi/Pb, Sn/Pb, Cr/Ni
26
Diagrammi di stato a due componenti
• La composizione
eutettica si solidifica a
temperatura minore di
tutte le altre
composizioni
• Questa più bassa
temperatura è detta
temperatura eutettica
(lega1) Liquido
Temperature eutettica
soluzione solida α + soluzione solida β
Raffreddamento
• Alla composizione eutettica 61.9 % Sn e appena sotto 183°C
Fasi presenti
Alfa
Beta
Composizione
19.2% Sn
97.5% Sn
Quantità di Fasi 97.5 –61.9 = 45.5%
61.9 -19.2
97.5 - 19.2
97.5 – 19.2
• Al punto c: 40% Sn e 230°C
Fasi presenti
Liquido
Composizione
48% Sn
Quantità di Fasi 40 –15
= 76%
48 – 15
Al punto d: 40% Sn e 183°C + ΔT
Fasi presenti
Liquido
Composizione
61.9% Sn
Quantità di Fasi
40 –19.2 = 49%
61.9 – 19.2
Alfa
15%Sn
48-40
48-15
= 54.5%
= 24%
•
Al punto e: 40% Sn e 183°C - ΔT
Fasi presenti
Alfa
Composizione
19.2% Sn
Quantità di Fasi
97.5 – 40 = 73%
97.5 – 19.2
Alfa
19.2%Sn
61.9 – 40 = 51%
61.9 – 19.2
•
Beta
97.5%Sn
40 – 19.2
97.5 – 19.2
= 27%
28
Diagrammi di stato Cu - Ag
P costante
29
Diagrammi di stato a due componenti
Reazione peritettica: la fase liquida reagisce con una fase solida per
formare una nuova e differente fase solida
Peritettico
Liquido + α
β
raffreddamento
•
A 42.4 % Ag e a 1400°C
Fasi presenti
Liquido
Alfa
Composizione
55% Ag
7%Ag
Quantità di Fasi
42.4 –7
55-42.4
55 – 7
55 - 7
= 74%
= 26%
•
A 42.4% Ag e 1186°C + ΔT
Fasi presenti
Liquido
Alfa
Composizione
66.3% Ag 10.5%Ag
Quantità di Fasi
42.4 –10.5 66.3-42.4
66.3 – 10.5 66.3–10.5
= 57%
=43%
•
A 42.4% Ag e 1186°C – ΔT
Fasi presenti
solo Beta
Composizione
42.4% Ag
Quantità di Fase
100%
•
A 60% Ag e 1150°C
Fasi presenti
Liquido
Composizione
77% Ag
Quantità di Fasi 60 – 48
77 – 48
= 41%
Beta
48%Ag
77 -30 60
77 – 48
= 59%