Statistica
STATISTICA
Ivan Zivko
Argomenti del corso
•
•
•
•
•
•
•
•
•
•
Distribuzioni statistiche e tabelle
Grafici
Misure di tendenza centrale (Medie)
Misure di dispersione
Rapporti statistici e numeri indice
Curva di Lorentz
Retta di regressione
Serie storiche
Campana di Gauss
…..
2
Docente: Ivan Zivko
1
Statistica
Introduzione
Popolazione
(Universo)
Unità
statistica
Abitanti
Svizzera
Persona
3
Introduzione: Tipi di variabili
• Le unità statistiche possono avere dei caratteri
o variabili che ne definiscono un aspetto, per
esempio:
– Colore degli occhi
– Altezza
– Stipendio
– Ecc.
4
Docente: Ivan Zivko
2
Statistica
Tipi di variabili
Variabili
(Caratteri)
Qualitative
Ordinabili
Non ordinabili
(Es.: Titolo
Studio)
(Es.: Colore
occhi)
Quantitative
Discrete
Continue
(Es.: Note)
(Es.: altezza)
5
Introduzione: Modalità
• Le modalità sono le possibili manifestazione di
una variabile. Esempi:
– Colore occhi: azzurri, verdi, marroni,…
– Nazionalità: svizzera, italiana,…
– Altezza: 170cm, 175cm,…
6
Docente: Ivan Zivko
3
Statistica
Distribuzioni statistiche
• Per rappresentare dei dati uno dei modi è usare
delle tabelle. Nella seguente per esempio
mostriamo le frequenze assolute:
Colore degli occhi
Frequenza assoluta
Azzurri
5
Verdi
3
Marroni
7
Scuri
2
TOTALE
17
7
Distribuzioni statistiche
• Un altro modo molto usato è quello di
rappresentare i dati tramite le frequenze
relative:
Colore degli occhi
Frequenza
assoluta
Frequenza
relativa
Azzurri
5
5/17=0.294=29.4
%
Verdi
3
0.176=17.6%
Marroni
7
0.411=41.1%
Scuri
2
0.118=11.8%
TOTALE
17
1=100%
8
Docente: Ivan Zivko
4
Statistica
Distribuzioni statistiche
• Un’altra distribuzione che può essere usata è la
frequenza cumulata, che può essere sia
assoluta che relativa.
Numero di figli
Frequenze relative
Freq. Relative
cumulate
1
40%
40%
2
30%
30%+40%=70%
3
20%
90%
>3
10%
100%
Totale
100%
9
Distribuzioni statistiche
• Oltre alle tabelle semplici viste fino ad adesso
se abbiamo più variabili contemporaneamente
possiamo rappresentarle in una tabella a
doppia entrata.
Sesso
Donne
Uomini
Totale
[20, 25[
21
24
45
[25, 30[
25
28
53
[30, 35[
15
31
46
Totale
61
83
144
Età
10
Docente: Ivan Zivko
5
Statistica
Distribuzioni statistiche:
suddivisione in classi
• Spesso i valori sono troppi, e non conviene
associare ad ognuno una modalità, perché i
dati sarebbero troppi e difficili da leggere.
• Molto spesso si impone quindi il
raggruppamento in classi.
11
Distribuzioni statistiche:
suddivisione in classi
• Per determinare il numero di classi ci sono 2
criteri possibili:
– Criterio della radice:
– Criterio di Sturges:
n. di classi n
n. di classi 1
10
log(n)
3
12
Docente: Ivan Zivko
6
Statistica
Distribuzioni statistiche:
suddivisione in classi, esempio
• Salario giornaliero di 40 dipendenti:
107
83
100
128
143
127
117
125
64
119
98
111
119
130
170
143
156
126
113
127
130
120
108
95
192
124
129
143
198
131
163
152
104
119
161
178
135
146
158
176
13
Distribuzioni statistiche:
suddivisione in classi, esempio
• Valore min.=64, Valore max=198.
– Il limite minore e quello superiore delle classi devono
contenere tutti i dati.
• Per esempio si può far partire la prima classe da
60 e l’ultima farla finire a 200.
– Il range sarà pertanto: 200-60=140.
• Per determinare il numero di classi usiamo il
criterio della radice: 40 6,3
– Si potrà creare 6-7 classi.
14
Docente: Ivan Zivko
7
Statistica
Distribuzioni statistiche:
suddivisione in classi, esempio
CLASSI
Freq. assolute
Freq. relative
[60, 80[
1
0.025
[80, 100[
3
0.075
[100, 120[
10
0.25
[120, 140[
12
0.30
[140, 160[
7
0.175
[160, 180[
5
0.125
[180, 200[
2
0.05
TOTALE
40
1
15
Grafici
• I grafici rispetto alle tabelle offrono una visione
immediata della situazione, permettendo una più
rapida memorizzazione e comprensione.
• La scelta del tipo di grafico dipende da fattori
soggettivi ma anche dal tipo di dati e dalla scala
di modalità impiegata.
16
Docente: Ivan Zivko
8
Statistica
Grafici a nastri o colonne
• I grafici a nastri o a colonne (o barre) vengono
usati soprattutto per variabili qualitative e
quantitative discrete.
17
Grafici a nastri o colonne
• Per ogni modalità del fenomeno vengono
disegnati rettangoli con larghezza generica e di
lunghezza proporzionale alla frequenza o
all’intensità.
• Esempio: ricavi di 5 negozi in un mese.
Docente: Ivan Zivko
NEGOZIO
Ricavi in euro
NEG. 1
21.750
NEG. 2
21.100
NEG. 3
20.550
NEG. 4
16.800
NEG. 5
19.700
18
9
Statistica
Grafici a nastri o colonne
NEG. 5
19,7
NEG. 4
16,8
NEG. 3
20,55
NEG. 2
21,1
NEG. 1
21,75
0
5
10
15
20
25
19
Grafici a nastri o colonne
25
21,75
21,1
20,55
19,7
20
16,8
15
10
5
0
NEG. 1
NEG. 2
NEG. 3
NEG. 4
NEG. 5
20
Docente: Ivan Zivko
10
Statistica
Grafici a nastri o colonne
• Questo tipo di grafico è possibile utilizzarlo
anche con tabelle a doppia entrata.
• Esempio 2:
ANNI
Importazioni
Esportazioni
1989
209.910
192.797
1990
217.703
203.515
1991
225.746
209.728
1992
232.111
219.436
1993
232.991
266.214
1994
270.063
305.479
21
Grafici a nastri o colonne
305,479
1994
270,063
266,214
1993
232,991
219,436
1992
232,111
209,728
1991
225,746
203,515
1990
217,703
192,797
1989
209,91
0
50
100
150
Esportazioni
200
250
300
350
Importazioni
22
Docente: Ivan Zivko
11
Statistica
Grafici a settori circolari o torta
• I grafici a settori circolari vengono usati per
mettere meglio in evidenza la suddivisione del
fenomeno fra le varie modalità che lo
compongono.
• Anche questo tipo di grafico è tipico per le
variabili qualitative e quantitative discrete.
• Gli angoli dei settori di ogni modalità si calcolano
col rapporto: i
fi
f i 360
360
f totale
i
f totale
23
Grafici a settori circolari o torta
• Consideriamo l’esempio dei ricavi dei 5 negozi:
NEG. 5 ; 19,7
NEG. 1 ; 21,75
NEG. 4 ; 16,8
NEG. 2 ; 21,1
NEG. 3 ; 20,55
24
Docente: Ivan Zivko
12
Statistica
Grafici a settori circolari o torta
• Se si vuole mettere in risalto la percentuale di
una delle modalità si può estrarre la rispettiva
fetta:
NEG. 1 ; 21,75
NEG. 5 ; 19,7
NEG. 4 ; 16,8
NEG. 2 ; 21,1
NEG. 3 ; 20,55
25
Grafici a settori circolari o torta
• Chiaramente le dimensioni della torta possono
variare, ma se rappresentano lo stesso
fenomeno le aree di una stessa modalità
saranno proporzionali tra loro.
• Un grafico a torta può rappresentare sia
frequenze assolute che relative.
26
Docente: Ivan Zivko
13
Statistica
Istogrammi
• Gli istogrammi vengono usati dove abbiamo
delle variabili continue, quindi quando i dati
vengono distribuiti in classi.
27
Istogrammi
• Esempio: nella seguente tabella abbiamo
suddiviso in classi il numero di treni rispetto al
loro ritardo.
RITARDO (min.)
N. TRENI
[0, 5[
24
[5, 10[
10
[10, 15[
7
[15, 20[
11
[20,25[
9
[25, 30[
4
28
Docente: Ivan Zivko
14
Statistica
Istogrammi
Treni in ritardo
30
25
frequenza
20
15
10
5
0
[0, 5[
[5, 10[
[10, 15[
[15, 20[
[20,25[
[25, 30[
Ritardo in minuti
29
Istogrammi
• Quando le classi non hanno ampiezza uguale
bisogna fare attenzione, perché l’altezza della
barra non sarà più uguale alla frequenza.
• Esempio 2: Numero di studenti rispetto ai mesi
che hanno passato a studiare.
Docente: Ivan Zivko
Mesi di studio
N. Studenti
(Freq. Assoluta)
Densità di
frequenza
[0, 1[
1634
1634/1=1634
[1, 3[
2184
2184/2=1092
[3, 6[
4920
4920/3=1640
[6, 12[
3384
3384/6=564
TOTALE
12122
30
15
Statistica
Istogrammi
• La frequenza assoluta è rappresentata
dall’area delle barre, l’altezza è la densità di
frequenza.
31
Istogrammi
• Gli istogrammi ci mostrano quindi
immediatamente la relazione tra l’ampiezza
della classe e la frequenza.
• Una classe piccola con meno frequenze
assolute può avere maggiore importanza di
una classe grande con più frequenze.
32
Docente: Ivan Zivko
16
Statistica
Istogrammi
• Esempio 2: libri venduti in una giornata per
classi di prezzo.
CLASSI DI PREZZO
(CHF)
NUMERO DI LIBRI
VENDUTI
DENSITÀ DI
FREQUENZA
[5, 15[
20
20/10=2
[15, 20[
15
15/5=3
[20, 35[
15
15/15=1
33
Istogrammi
34
Docente: Ivan Zivko
17
Statistica
Diagrammi cartesiani
• Per rappresentare l’andamento di un fenomeno
al variare di un parametro si usano punti nel
piano cartesiano legati da segmenti, questi
grafici sono i diagrammi cartesiani.
• Si usano per variabili quantitative e qualitative
ordinabili.
35
Diagrammi cartesiani
• Esempio: distribuzione delle persone che si
sono recate in poliambulatorio in una
settimana:
Sesso
Uomini
Donne
Totale
Lunedì
31
23
54
Martedì
35
47
82
Mercoledì
33
42
75
Giovedì
19
40
59
Venerdì
31
39
70
TOTALE
149
191
340
Giorni
36
Docente: Ivan Zivko
18
Statistica
Diagrammi cartesiani
90
80
70
60
50
Uomini
Donne
40
Totale
30
20
10
0
Lunedì
Martedì
Mercoledì
Giovedì
Venerdì
37
Forma dei grafici
• Sia che rappresentiamo le frequenze con un
grafico a barre, un istogramma o un diagramma
cartesiano, possiamo definire alcuni tipi di
comportamenti a dipendenza della forma che
assume il grafico.
38
Docente: Ivan Zivko
19
Statistica
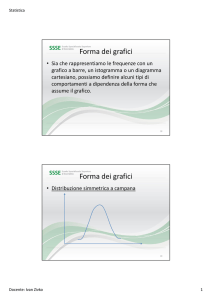
Forma dei grafici
• Distribuzione simmetrica a campana
39
Forma dei grafici
• Distribuzione positivamente asimmetrica
40
Docente: Ivan Zivko
20
Statistica
Forma dei grafici
• Distribuzione negativamente asimmetrica
41
Forma dei grafici
• Distribuzione ascendente
42
Docente: Ivan Zivko
21
Statistica
Forma dei grafici
• Distribuzione discendente
43
Forma dei grafici
• Distribuzione ad “U”
44
Docente: Ivan Zivko
22
Statistica
Forma dei grafici
• Distribuzione bimodale
45
Forma dei grafici
• Distribuzione plurimodale
46
Docente: Ivan Zivko
23
Statistica
L’ogiva
• Se rappresentiamo con un istogramma le
frequenze relative cumulate invece delle
frequenze assolute otteniamo un grafico
crescente.
• Se poi uniamo gli spigoli delle barre con dei
segmenti otteniamo un’ogiva.
47
L’ogiva
• Esempio: punti ottenuti da degli studenti in un
test attitudinale.
CLASSI
(PUNTI)
N. STUDENTI
(Freq. Assoluta)
Freq. RELATIVA
Freq. RELATIVA
CUMULATA
[900, 1400[
8
35%
35%
[1400, 1900[
7
30%
65%
[1900, 2400[
6
26%
91%
[2400, 2900[
2
9%
100%
48
Docente: Ivan Zivko
24
Statistica
L’ogiva
Frequenze cumulate
120%
100%
Percentuale studenti
80%
60%
40%
20%
0%
[0, 900[
[900, 1400[
[1400, 1900[
[1900, 2400[
[2400, 2900[
Punti
49
L’ogiva
• Con questo grafico possiamo per esempio dire
che percentuale di dati si trova al di sotto di
un certo valore.
• Si può anche determinare quanti dati si
trovano in un certo intervallo.
50
Docente: Ivan Zivko
25
Statistica
Misure di tendenza centrale
Misure di tendenza centrale
Medie ferme
Medie di posizione
* Media aritmetica
* Moda
* Media geometrica
* Mediana
Ecc.
51
Medie ferme
• Le medie ferme si calcolano usando tutti i
valori a disposizione.
• Rischio: è possibile che valori molto alti o
molto bassi con poca frequenza possano
falsare il valore centrale, o meglio quello
rappresentativo dei dati.
52
Docente: Ivan Zivko
26
Statistica
Medie Ferme: media aritmetica
• È la somma di tutti i valori diviso il loro
numero totale.
• Media aritmetica:
x f x f .... xn f n
x 1 1 2 2
N
n
x f
i
i
i 1
N
53
Medie Ferme: media aritmetica
• Esempio 1: considera le note di 5 studenti:
– 3, 4, 5.5, 6, 4.5.
3 4 5.5 6 4.5 23
x
4.6
5
5
54
Docente: Ivan Zivko
27
Statistica
Medie Ferme: media aritmetica
• Osservazione: la media aritmetica si può
calcolare disponendo anche solo delle
frequenze relative.
x1 f1 .... xn f n
f
f
x1 1 ...xn n
N
N
N
x1 f rel .1 ... xn f rel .n
x
55
Medie Ferme: media aritmetica
• Esempio 2: se i dati sono molti e dobbiamo
suddividerli in una tabella bisognerà usare le
frequenze.
NOTE
N. Studenti (Freq.
Freq. relativa
Assoluta)
3
4
0.17
4
6
0.25
4.5
8
0.33
5
3
0.125
5.5
2
0.083
6
1
0.042
TOTALE
24
1
56
Docente: Ivan Zivko
28
Statistica
Medie Ferme: media aritmetica
• Esempio 2: per calcolare la media aritmetica si
possono usare sia le frequenze assolute che
quelle relative.
3 4 4 6 4.5 8 5 3 5.5 2 6 1 104
x
4.33
24
24
x 0.17 3 0.25 4 0.33 4.5 0.125 5 0.083 5.5 0.042 6 4.33
57
Medie Ferme: media aritmetica
• Se i dati sono suddivisi in classi per calcolare la
media aritmetica bisogna prendere i valori
centrali delle classi.
• Esempio 3: salario dei dipendenti.
Classi di stipendio (in
migliaia di CHF)
Numero dipendenti
(Freq. Assoluta)
Centro classi
[50, 60[
10
55
[60, 70[
20
65
[70, 80[
15
75
TOTALE
45
x
Docente: Ivan Zivko
55 10 65 20 75 15 2975
66.11
45
45
58
29
Statistica
Medie Ferme: media aritmetica
• È chiaro che suddividendo i dati in classi
perdiamo delle informazioni, e quindi
commetteremo un piccolo errore.
• L’errore dovuto all’uso delle classi sarà:
a
err.
2x a
59
Medie Ferme: media aritmetica
• La media aritmetica ha in genere una buona
stabilità, che cresce con l'aumentare dei dati.
• Quando nei dati ci sono valori estremi
particolarmente „pesanti“ la media aritmetica
può essere molto influenzata da essi anche se
in realtà non hanno una grande frequenza.
60
Docente: Ivan Zivko
30
Statistica
Medie Ferme: media geometrica
• La media geometrica viene usata per dati che
variano in progressione temporale, per
esempio per gli indici.
• Media geometrica:
f1
f2
x x1 x2 .... xnf n
N
61
Medie Ferme: media geometrica
• Esempio: È dato un bene di valore C. Questo
bene nel primo anno aumenta il valore dell’ 8%,
nel secondo del 12%, nel terzo del 9% e nel
quarto del 5%. Si vuole trovare l’aumento
percentuale medio. Da ciò si possono trovare i
moltiplicatori:
M 1 C (1 0.08)
M 2 M 1 (1 0.12) C (1 0.08) (1 0.12)
ecc.
62
Docente: Ivan Zivko
31
Statistica
Medie Ferme: media geometrica
• Quindi alla fine dei quattro anni l’aumento si
calcolerà come segue:
C (1 0.08) (1 0.12) (1 0.09) (1 0.05)
C 1.08 1.12 1.09 1.05 C 1.3843872
• Il moltiplicatore medio sarà:
4
1.3843872 1.0847
Che equivale a un aumento percentuale annuo
del
0.0847 8.47%
63
Medie Ferme: media geometrica
• Se avessimo fatto la media aritmetica
avremmo ottenuto un aumento dell’8.5%.
• Se per ogni anno usiamo questo aumento non
otteniamo il risultato esatto.
64
Docente: Ivan Zivko
32
Statistica
Medie di posizione
• Come detto quando ci sono valori estremi troppo
grandi la media aritmetica non va più bene.
• Non possiamo semplicemente non tenere conto di
questi valori, perchè non seguiremmo i principi
fondamentali della statistica.
• A differenza delle medie ferme con le medie di
posizione possiamo anche cercare il valore medio di
variabili qualitative.
65
Medie di posizione: Moda
• La moda è quella media che viene associata alla
modalità con frequenza più alta.
• Essa è tanto più esatta quanto più la sua frequenza
è elevata rispetto alle altre (se è maggiore del 50%
è molto buona).
• Se le frequenze sono simili la moda perde la sua
efficacia. Se ci sono due modalità con frequenza
uguale si dice che la classe è bimodale.
66
Docente: Ivan Zivko
33
Statistica
Medie di posizione: Moda
• Esempio 1: colore dei capelli di un gruppo.
Colore capelli
Frequenza
assoluta
Castani
70
Biondi
30
Rossi
30
Altro
10
Moda Castani
67
Medie di posizione: Moda
• Il calcolo diventa un po’ più complicato se
abbiamo dei dati suddivisi in classi.
• Prima di tutto bisogna determinare la classe
modale, che è semplicemente la classe con
frequenza più elevata.
• Per trovare il valore modale si userà la formula
poi:
1
Moda Linf .
a
1 2
68
Docente: Ivan Zivko
34
Statistica
Medie di posizione: Moda
Linf . Limite inferiore della classe modale
1 (Freq. assoluta classe modale) (Freq. ass. classe precedente)
2 (Freq. assoluta classe modale) (Freq. ass. classe successiva)
a ampiezza delle classi
69
Medie di posizione: Moda
• Esempio 2: altezze di un gruppo.
Classi (Altezza)
Freq. assoluta
[158, 162[
4
[162, 166[
7
[166, 170[
13
[170, 174[
18
[174, 178[
8
Totale
50
70
Docente: Ivan Zivko
35
Statistica
Medie di posizione: Moda
• La classe modale è la classe [170, 174[.
Usando la formula:
(18 13)
5
4 170
4
(18 13) (18 8)
5 10
5
170 4 170 1.333 171.333
15
Moda 170
71
Medie di posizione: Mediana
• Si definisce mediana di un insieme di elementi,
disposti in ordine crescente o decrescente, il
valore che occupa la posizione centrale.
• Esempio 1: se il numero di elementi è dispari.
8, 12, 7, 4, 9, 10, 55
Bisogna prima metterli in ordine crescente.
4, 7, 8, 9, 10, 12, 55
Mediana 9
Docente: Ivan Zivko
72
36
Statistica
Medie di posizione: Mediana
• Esempio 2: se il numero di elementi è pari.
36, 72, 82, 84, 98, 105
I due valori centrali sono 82 e 84, perciò:
Mediana
82 84
83
2
73
Medie di posizione: Mediana
• Se i dati sono molti, e quindi vengono
rappresentati in una tabella per determinare la
mediana si guardano le frequenze cumulate.
• La mediana è quella modalità in cui la
frequenza cumulata supera il 50%.
74
Docente: Ivan Zivko
37
Statistica
Medie di posizione: Mediana
• Esempio 3: numero di interrogazioni per
studente.
Numero
interrogazioni
Freq. assoluta
Freq. cumulata
0
3
3
1
6
9
2
4
13
3
2
15
Totale
75
Medie di posizione: Mediana
• Esempio 3: in questo caso la frequenza
cumulata viene superata nella seconda
modalità, quindi:
Mediana 1
76
Docente: Ivan Zivko
38
Statistica
Medie di posizione: Mediana
• Se i dati sono suddivisi in classi bisogna prima di
tutto determinare la classe mediana, che è la
classe in cui la frequenza cumulata supera il
50%.
• Poi per trovare il valore mediano si userà la
formula:
N
f cumulata classe precedente
Mediana Linf . 2
f classe mediana
a
77
Medie di posizione: Mediana
• Esempio 3: prendiamo l’esempio delle altezze.
Classi (Altezza)
Freq. assoluta
Freq. cumulata
[158, 162[
4
4
[162, 166[
7
11
[166, 170[
14
25
[170, 174[
17
42
[174, 178[
8
50
Totale
50
78
Docente: Ivan Zivko
39
Statistica
Medie di posizione: Mediana
• La classe mediana è la classe [170, 174[.
Usando la formula:
50
11
25 11
Mediana 166 2
4 166
4
14
14
14
166 4 170
14
79
Misure di dispersione
• Le medie da sole non ci dicono molto sulla
distribuzione dei dati.
• Ci servono delle misure che ci dicano quanto i
dati sono dispersi intorno alle medie.
• La misura più importanti sono:
– Rango (o campo di variazione)
– Semidifferenza interquartile (per la mediana)
– Scostamento semplice assoluto
– Scarto quadratico medio (o deviazione standard)
80
Docente: Ivan Zivko
40
Statistica
Rango (campo di variazione)
• È la differenza tra il valore più alto e quello più
basso.
Rango Valore Max Valore Min
• Esempio: età di 6 persone: 45, 48, 51, 77, 81, 90.
r 90 45 45
81
Rango (campo di variazione)
• Si usa quando si vuole mettere in evidenza la
differenza tra il valore massimo e quello minimo
di una distribuzione, come per esempio la
differenza tra il peso massimo e minimo di un
gruppo di persone.
• Da solo non ci da abbastanza informazione sulla
dispersione dei dati.
82
Docente: Ivan Zivko
41
Statistica
Semidifferenza interquartile
• Abbiamo visto che la mediana corrisponde al
valore che si situa al 50% dei dati.
• Se dividiamo i dati in 4 parti abbiamo i
quartili!
Q1 primo quartile (25% dei dati)
Q 2 secondo quartile (50% dei dati) Mediana
Q 3 terzo quartile (75% dei dati)
Q 4 quarto quartile (100% dei dati)
83
Semidifferenza interquartile
• Questa misura si usa solo per la mediana.
• Il calcolo è il seguente:
Q3 Q1
s
2
• Il 50% dei dati si trova nell’intervallo
Mediana s
84
Docente: Ivan Zivko
42
Statistica
Semidifferenza interquartile
• Esempio: immagina semplicemente di avere 20
dati:
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
• La mediana corrisponde a 10.5.
• Mentre
=5
= 15, perciò la
semidifferenza interquartile è s 15 5 10 5
2
2
• Significa che circa il 50% dei dati si trova tra 5.5 e
15.5.
85
Semidifferenza interquartile
• Esempio 2: se i dati sono suddivisi in classi
come prima cosa bisogna guardare le
frequenze cumulate relative.
Classi (Altezza)
Freq. assoluta
Freq. cumulata Freq. Cum. Rel.
[158, 162[
4
4
8%
[162, 166[
9
13
26%
[166, 170[
13
26
52%
[170, 174[
16
42
84%
[174, 178[
8
50
100%
Totale
50
86
Docente: Ivan Zivko
43
Statistica
Semidifferenza interquartile
• Esempio 2:
Q1 164, Q3 172
172 164 8
s
4
2
2
87
Scostamento medio semplice
• È la media degli scostamenti!
• Esempio: considera cinque valori: 2, 2, 6, 6, 9.
Media
SM
22669
5
5
25 25 65 65 95
5
3 3 11 4
2.4
5
88
Docente: Ivan Zivko
44
Statistica
Scarto quadratico medio
(Deviazione standard)
• La deviazione standard è la misura di dispersione
più usata in assoluto.
M-σ
M
M+σ
• Almeno il 68% dei dati si trova in questo
intervallo.
89
Scarto quadratico medio
(Deviazione standard)
• Se M è la media, allora definiamo come
varianza:
2
2
2
x1 M f1 x2 M f 2 .... xn M f n
2
N
• La deviazione standard è la sua radice
quadrata:
Dev. standard 2
90
Docente: Ivan Zivko
45
Statistica
Scarto quadratico medio
(Deviazione standard)
• Esempio: ospiti di un albergo per numero di
pernottamenti.
N. Notti
Frequenza
5
39
6
30
7
13
8
5
9
3
M Media 6
91
Scarto quadratico medio
(Deviazione standard)
• Calcoliamo la varianza:
2
5 62 39 6 62 30 7 62 13 8 62 5 9 62 3
90
1.1
• E quindi la deviazione standard è:
1.1 1.049 1
• Almeno il 68% dei dati si troverà nell’intervallo:
6 1
Docente: Ivan Zivko
92
46
Statistica
Dati standardizzati
• Per confrontare dati che fanno parte di serie diverse
bisogna che siano standardizzati rispetto alle
rispettive medie e allo scarto tipo.
• Esempio: uno studente all’esame di fisica ha preso
4.5, la media della classe era 4.2 e lo scarto tipo 0.9.
Lo stesso studente a matematica prende 5, ma la
media è 4.7 e lo scarto 1.2. Qual’ è il voto
relativamente migliore?
93
Dati standardizzati
• Per prima cosa vediamo quanto meglio ha fatto
rispetto alla media della classe nelle due materie:
FISICA
MATEMATICA
4.5 4.2 0.3
5 4.7 0.3
• Questo dato va però normalizzato rispetto allo
scarto tipo:
FISICA
0. 3
0.333
0.9
MATEMATICA
0.3
0.25
1.2
94
Docente: Ivan Zivko
47
Statistica
Dati standardizzati
• Più lo scarto tipo è alto e più ci saranno
studenti che si allontanano dalla media, e
quindi che hanno fatto anche meglio del
nostro studente.
• Lo studente ha fatto quindi relativamente
meglio l’esame di fisica.
95
Rapporti statistici: rapporto di
coesistenza
• I rapporti di coesistenza mettono a confronto due
fenomeni diversi relativi allo stesso tempo e luogo.
• Esempio: un agenzia turistica organizza un tour, al
quale partecipano 302 donne e 208 uomini. Il
rapporto di coesistenza è: 302
208
1.45
• Moltiplicando per abbiamo: 1.45 100 145
Significa che ci sono 145 donne ogni 100 uomini.
96
Docente: Ivan Zivko
48
Statistica
Rapporti statistici:
rapporto di durata e ripetizione
• I rapporti di durata e ripetizione sono rapporti
utili per descrivere le variazioni quantitative
subite da un certo fenomeno (es.: scorte in
magazzino che si rinnovano, variazioni di degenti
in ospedale, ecc.).
• Rapporto di durata:
C0 presenze all' inizio
C1 presenze alla fine
d
C0 C1
E U
U uscite
E entrate
97
Rapporti statistici:
rapporto di durata e ripetizione
• In un negozio, che resta aperto 8 ore, al
momento dell’apertura ci sono 100 (C0) persone.
Durante il giorno ne sono entrate altre 950 (E) e
uscite 750 (U).
C1 100 950 750 300
d
100 300 400
0.235 1.88 ore
950 750 1700
98
Docente: Ivan Zivko
49
Statistica
Rapporti statistici:
rapporto di durata e ripetizione
• Rapporto di ripetizione:
• Dall’esempio:
r
1
r
d
1
4.25
0.235
ciò significa che le persone all’interno del
negozio si rinnovano completamente 4.25 volte
nel corso della giornata.
99
Numeri indice
• I numeri indice sono dei rapporti statistici che
evidenziano le variazioni, temporali o spaziali, di un
fenomeno.
• Si calcolano eseguendo il rapporto dei dati di una
serie per uno di essi (detto base). Si possono quindi
distinguere in:
– Numeri indice semplici a base fissa.
– Numeri indice semplici a base mobile.
– Numeri indice composti.
100
Docente: Ivan Zivko
50
Statistica
Numeri indice: applicazioni
• Il costo della vita (indice dei prezzi al consumo)
• Costo della produzione industriale
• Evoluzione della massa monetaria
• …
101
Numeri indice: costruzione
• Per trasformare una serie di valori in indici
dobbiamo prima di tutto scegliere un valore che
funga da base.
• In seguito dividere tutti gli altri valori per la
base, e eventualmente moltiplicare per 100.
102
Docente: Ivan Zivko
51
Statistica
Numeri indice: tipologia
• Le tipologie più usate di numeri indice sono:
– Indice dei prezzi
– Indice delle quantità (produzione, consumo,..)
– Indice del valore
103
Numeri indice: costruzione
• Esempio 1: Il prezzo di un certo bene nel 1980 era di
20 Fr., nel 1981 di 24 Fr. e nel 1982 di 25 Fr..
Se prendiamo come base il prezzo del 1980 avremo:
20
=
100 = 100
,
20
,
=
24
100 = 120
20
,
=
25
100 = 125
20
104
Docente: Ivan Zivko
52
Statistica
Numeri indice: costruzione
• Esempio 2:una ditta ha esportato nel 1980 32000 t
di cereali, nel 1981 29000 t e nel 1982 34000 t.
Prendendo come base la quantità del 1980:
32000
=
100 = 100
,
32000
,
,
=
29000
100 ≈ 91
32000
=
34000
100 ≈ 106
32000
105
Numeri indice: costruzione
• Esempio 3:una ditta nel 1980 ha esportato
32000 t di cereali a 60 Fr la tonnellata, mentre
nel 1981 solamente 29000 t a 62 Fr la tonnellata.
L’indice del valore con base 1980 sarà:
,
=
29000 62
100 =≈ 94
32000 60
106
Docente: Ivan Zivko
53
Statistica
Numeri indice a base fissa
• Esempio 4: produzione di lavatrici e
lavastoviglie in alcuni anni.
Anni
Lavatrici prodotte
Indici (base=1991)
1991
5’043’983
100
1992
5’140’277
102
1993
5’692’505
113
1994
6’251’283
124
1995
6’995’818
139
107
Numeri indice a base fissa
• Esempio 4:
Anni
Lavastoviglie
prodotte
Indici (base=1991)
1991
950’940
100
1992
937’720
99
1993
1’141’861
120
1994
1’464’885
154
1995
1’683’093
177
108
Docente: Ivan Zivko
54
Statistica
Numeri indice a base fissa
• Esempio 4:
190
180
170
160
150
140
Lavatrici
Lavastoviglie
130
120
110
100
109
90
1991
1992
1993
1994
1995
Numeri indice a base mobile
• Spesso invece di evidenziare l’andamento di
un fenomeno rispetto a un solo anno, si vuole
studiare la variazione di ogni dato rispetto
all’anno precedente.
• La base diventa il valore dell’anno precedente.
Si parla di base mobile.
110
Docente: Ivan Zivko
55
Statistica
Numeri indice a base mobile
• Esempio 5: consideriamo i dati dell’esempio 4 e
prendiamo come base l’anno precedente.
Anni
Indici lavatrici
base mobile
Indici lavastoviglie base
mobile
1991
-
-
1992
102
99
1993
111
122
1994
110
128
1995
112
115
111
Numeri indice a base mobile
• Esempio 5:
130
125
120
115
110
Lavatrici
Lavastoviglie
105
100
95
90
1992
Docente: Ivan Zivko
1993
1994
1995
112
56
Statistica
Numeri indice: proprietà
• Le seguenti proprietà valgono se gli indici non
sono ancora stati moltiplicati per 100.
• Proprietà di simmetria:
I 0,1
1
I1,0
• Proprietà transitiva: I 4, 0 I 4,3 I 3, 2 I 2,1 I1, 0
113
Numeri indice: cambiamento di base
• Per trasformare una serie di indici da una base
ad un’altra bisogna dividere tutti gli indici per
quello dell’anno che desidero usare come base.
114
Docente: Ivan Zivko
57
Statistica
Numeri indice: cambiamento di base
• Esempio: sono dati gli indici concernenti lo
sviluppo della cifra d’affari di due apparecchi.
ANNO
INDICE
App. A
Anno base=2000
App. B
Anno base=2002
2000
100
--
2001
108
--
2002
112
100
2003
117
108
2004
124
114
115
Numeri indice: cambiamento di base
• Per poter confrontare le due serie di dati
dobbiamo trasformare tutto nella stessa base,
che in questo caso deve essere l’anno 2002:
100
100 89
112
108
I 01/ 02
100 96
112
112
I 02 / 02
100 100
112
117
I 03 / 02
100 104
112
124
I 00 / 02
100 111
112
I 00 / 02
Docente: Ivan Zivko
116
58
Statistica
Numeri indice: cambiamento di base
• Adesso i dati sono confrontabili:
ANNO
INDICE
App. A
Anno base=2002
App. B
Anno base=2002
2000
89
--
2001
96
--
2002
100
100
2003
104
108
2004
111
114
117
Numeri indice
aggregati, semplici e ponderati
• Spesso gli indici sono composti da più fattori,
per esempio l’indice dei prezzi è composto dai
prezzi di più beni (es.: pane, latte, …). Per
esempio se l’anno base è 1:
p2,1
p
p
i,2
i ,1
118
Docente: Ivan Zivko
59
Statistica
Numeri indice
aggregati, semplici e ponderati
• Calcolare gli indici aggregati ponderati significa
moltiplicare i prezzi per le quantità, quindi
l’indice dei valori:
I 2,1
p
p
i,2
qi , 2
i ,1
qi ,1
119
Numeri indice
aggregati, semplici e ponderati
• Esempio: prezzo e quantità prodotta di
fitofarmaci tra il 2000 e il 2001:
Prodotti
Prezzo
(Fr. per pezzo)
2000
Prezzo
(Fr. per pezzo)
2001
Quantità
(in migliaia)
2000
Quantità
(in migliaia)
2001
Anticrittogamici
2
3
67
72
Diserbanti
2.5
3
35
29
Insetticidi
2
1
22
27
120
Docente: Ivan Zivko
60
Statistica
Numeri indice
aggregati, semplici e ponderati
• Volendo calcolare l’indice ponderato dei
fitofarmaci tra 2000 e 2001 potremmo fare:
I 2,1
p
p
i ,1
qi ,1
i ,0
qi ,0
3 72 3 29 1 27
2 67 2.5 35 2 22
330
1.24 124
265.5
121
Numeri indice
aggregati, semplici e ponderati
• In realtà ci sono alcuni metodi particolari usati
per il calcolo degli indici:
– Indice di Laspeyeres: metodo dell’anno base
– Indice di Paasche: metodo dell’anno dato
– Metodo dell’anno tipico (la quantità base è la media
delle quantità)
– Indice di Fisher: media geometrica tra Laspeyeres e
Paasche
122
Docente: Ivan Zivko
61
Statistica
Numeri indice
aggregati, semplici e ponderati
• Indice di Laspeyeres: si prende sempre la
quantità dell’anno base.
IL
3 67 3 35 1 22
328
1.235 123.5
2 67 2.5 35 2 22 265.5
123
Numeri indice
aggregati, semplici e ponderati
• Indice di Paasche: si prende sempre la quantità
dell’anno dato.
IP
3 72 3 29 1 27
330
1.22 122
2 72 2.5 29 2 27 270.5
124
Docente: Ivan Zivko
62
Statistica
Numeri indice
aggregati, semplici e ponderati
• Indice di Fisher: si fa la media geometrica tra
l’indice di Laspeyeres e Paasche:
I F 123.5 122 15067 122.75
125
Misura di concentranzione
• Una misura di concentrazione serve in statistica
per verificare in che modo un certo bene è
diviso tra la popolazione, oppure per misurare la
presenza di un prodotto o di impresa in un certo
territorio.
126
Docente: Ivan Zivko
63
Statistica
Misura di concentrazione
• Esempio: distribuzione di un pacchetto azionario
fra gli azionisti. Cerchiamo di stabilire se le azioni
sono distribuite equamente o no.
Classi azioni
Frequenze
Ammontare azioni
[0, 10[
250
1250
[10, 20[
400
6000
[20, 30[
190
4750
[30, 40[
100
3500
[40, 50[
40
1800
Oltre 50
20
1400
Totale
1000
18700
127
Misura di concentrazione
• Trasformiamo i dati in percentuali, e poi ricaviamo
le percentuali cumulate:
Docente: Ivan Zivko
Classi azioni
Percentuale
azionisti
Perc.
cumulata
azionisti
Percentuale
azioni
Perc.
cumulata
azioni
[0, 10[
25
25
6.68
6.68
[10, 20[
40
65
32.08
38.76
[20, 30[
19
84
25.4
64.16
[30, 40[
10
94
18.72
82.88
[40, 50[
4
98
9.63
92.51
Oltre 50
2
100
7.49
100
Totale
100
100
128
64
Statistica
Misura di concentrazione
• Dalla tabella possiamo ottenere per esempio le
seguenti informazioni:
– Il 65% degli azionisti possiede il 38.76% delle azioni
– L’84% degli azionisti possiede il 64.16% delle azioni
– Ecc.
129
Misura di concentrazione
• Possiamo rappresentare la situazione bene con un
diagramma cartesiano, che in questo caso viene
chiamato anche curva di concentrazione o curva
di Lorentz.
% Azioni cumulate
120
100
80
60
40
20
0
0
Docente: Ivan Zivko
20
40
60
80
100
120
130
65
Statistica
Misura di concentrazione
• Nel caso di equidistribuzione tutti gli azionisti
dispongono di uno stesso numero di azioni: per
esempio il 25% degli azionisti possiede il 25%
delle azioni, ecc.. Retta di equidistribuzione:
120
100
80
60
40
20
0
0
20
40
60
80
100
120
131
Misura di concentrazione
• Più la curva di Lorentz si avvicina alla retta di
equidistribuzione, più i beni sono divisi
equamente tra la popolazione.
132
Docente: Ivan Zivko
66
Statistica
Retta di regressione
• Spesso si desidera analizzare l’andamento di una
variabile rispetto al tempo oppure rispetto a
un’altra variabile.
• Se un minimo legame effettivamente esiste è
possibile ricavare la retta di regressione, che ci
permette inoltre di fare previsioni.
133
Retta di regressione
• Esempio: esportazioni ed importazioni in milioni
di dollari di alcuni paesi nel 1986.
PAESE
Importazioni
Esportazioni
Danimarca
22.8
22.1
Irlanda
11.6
12.6
Olanda
75.4
80.6
Svizzera
40.9
37.3
Italia
100
97.5
Svezia
32.5
37.5
Portogallo
9.4
7.2
134
Docente: Ivan Zivko
67
Statistica
Retta di regressione
120
100
ESPORTAZIONI
80
60
40
20
0
0
20
40
60
IMPORTAZIONI
80
100
120
135
Retta di regressione
• Un equazione generale di una retta ha la
seguente forma:
y axb
a pendenza della retta
b intersezione della retta con l' asse y
136
Docente: Ivan Zivko
68
Statistica
Retta di regressione: Covarianza
• Per poter calcolare la retta di regressione
dobbiamo prima calcolare la covarianza, un
valore che lega due variabili X e Y.
• Siano x1, x2, …, xn i valori della prima variabile e
Mx la loro media, rispettivamente y1,.., yn i valori
della seconda variabile e My la loro media:
xy
( x1 M x ) ( y1 M y ) ( x2 M x ) ( y2 M y ) ....
n
n
(x M
i
x
) ( yi M y )
i 1
n
137
Retta di regressione
• Quindi per determinare la retta noi dobbiamo
determinare a e b.
Cov ( x, y ) xy
a
2
Var ( x)
x
b My aMx
138
Docente: Ivan Zivko
69
Statistica
Retta di regressione
• Riprendiamo l’esempio sulle esportazioni e
importazioni e calcoliamo la retta di regressione.
xy 995.234
a
x 2 989.47
995.234
1.0058
989.47
b 42.11 41.8 1.0058 0.0676
139
Retta di regressione
• Quindi otteniamo:
y 1.0058 x 0.0676
• Questa retta approssima i punti, e permette di
fare delle previsioni, per esempio come
sarebbero le esportazioni se le importazioni
fossero 120 milioni di dollari:
y 1.0058 120 0.0676 120.8
140
Docente: Ivan Zivko
70
Statistica
Retta di regressione
120
100
y = 1,0058x + 0,0708
ESPORTAZIONI
80
60
40
20
0
0
20
40
60
80
100
120
IMPORTAZIONI
141
142
Docente: Ivan Zivko
71
Statistica
Serie storiche
• Una serie storica è la classificazione di una
variabile rispetto al tempo.
• Le serie storiche vengono studiate sia per
interpretare un fenomeno, individuando
componenti di trend, di ciclicità, di stagionalità
e/o di accidentalità, sia per prevedere il suo
andamento futuro.
143
Serie storiche
• Esempi di fenomeni analizzabili con serie
storiche sono:
– Numero di dipendenti di un azienda
– Indice dei prezzi
– PIL
– Vendite
– …..
144
Docente: Ivan Zivko
72
Statistica
Serie storiche
• Esempio: PIL italiano trimestrale dal 1981 al
2008
145
Serie storiche
• Il movimento tendenziale (o trend) della serie
indica il suo andamento crescente o
decrescente nel tempo, senza considerare le
possibili fluttuazioni (vedi per esempio la retta
di regressione).
• Riguarda l’andamento sul lungo periodo
(diversi anni).
146
Docente: Ivan Zivko
73
Statistica
Serie storiche
• Il movimento ciclico della serie indica le
fluttuazioni periodiche o non periodiche attorno
alla curva di trend con durata pluriannale (ciclo
economico).
• Riguarda l’andamento sul medio periodo
(qualche anno).
147
Serie storiche
• Questo movimento può essere suddiviso in 4
fasi del ciclo economico (movimenti
congiunturali):
– Prosperità: aumento superiore a quello dell’anno
precedente.
– Recessione: aumento inferiore a quello dell’anno
precedente.
– Crisi: diminuzione negativa superiore a quella
dell’anno precedente.
– Ripresa: diminuzione negativa inferiore a quella
dell’anno precedente.
148
Docente: Ivan Zivko
74
Statistica
Serie storiche
• Il movimento stagionale rappresenta il ripetersi
di situazioni che fanno variare l’andamento
della serie con oscillazioni più o meno forti
negli stessi periodi dell’anno. Ad esempio
l’aumento del consumo di carburante in inverno
o la diminuzione della produzione in estate.
• Riguarda quindi l’andamento sul breve periodo.
149
Serie storiche
• Il movimento accidentale provoca oscillazioni
dovute ad eventi casuali come scioperi,
calamità naturali o concorrenza non prevista.
150
Docente: Ivan Zivko
75
Statistica
Teoria dei campioni
• Quando si vogliono rilevare dei dati, per ricavare
delle informazioni o fare previsioni, lo si fa di
solito su di un campione statistico e non
sull’intera popolazione, perché troppo
numerosa.
151
Teoria dei campioni
• È importante definire i criteri e le modalità per
l’estrazione del campione, infatti è indispensabile
che il campione sia rappresentativo della
popolazione in relazione alla variabile indagata.
• Se per es. si vuole valutare il reddito medio dei
lavoratori di una città bisogna che nel campione
tutte le categorie siano rappresentate nelle
percentuali giuste.
152
Docente: Ivan Zivko
76
Statistica
Teoria dei campioni
• Per ottenere dei campioni rappresentativi si può
procedere con un campionamento casuale.
• Per ottenere ciò a ogni elemento dell’universo si
assegna un numero progressivo, si ricorre poi a
una tavola dei numeri casuali oppure
all’estrazione.
153
Teoria dei campioni
• Esempio: si vuole campionare il peso di 14
lamine, estratte da un universo di 1500.
154
Docente: Ivan Zivko
77